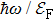In recent decades, significant effort has been dedicated to the study of topological insulators (TIs) and low-dimension semimetals like graphene. In the low-energy limit, the electrons in these exotic materials obey relativistic, Dirac-like Hamiltonians. Their pseudo-massless particle behavior confers these materials unique optical properties such as high electromagnetic field confinement^[1–4] and strong optical nonlinearity,^[5–16] making them desirable for uses like table-top generation of high-brightness coherent radiation spanning from the x-ray to the terahertz regimes through mechanisms such as free-electron-graphene plasmon scattering,^[17,18] high-harmonic generation,^[19–22] and transition radiation,^[23] and also as saturable absorbers for infrared ultrafast lasers.^[24–27]

Recently, a new class of quantum materials which behave like the bulk analogues of graphene have also attracted significant attention – 3D Dirac semimetals (DSMs). Unlike their TI counterparts which possess only conducting surface states, 3D DSMs are also conducting in the bulk. The dispersion of 3D DSMs is formed from a superposition of two Weyl cones of opposite chiralities.^[29,28] Each Weyl cone is linearly dispersing in all three momentum directions and is doubly-degenerate at a single band-touching point (Weyl node). Hence, the energy bands are doubly-degenerate for all momenta except at the Dirac point, where a four-fold degeneracy arises from the overlap of two Weyl nodes. Topologically unprotected Dirac points may occur at a quantum critical point in the phase transition between a TI and a normal insulator^[30–36] or between weak and strong TIs.^[37] Some Dirac points are guaranteed by virtue of crystal symmetries^{[29,30,38,39]} and unlike graphene, are robust against spin–orbit interaction-induced gapping. These stable Dirac points have been predicted in materials like BiO₂^[38] and A₃Bi (A = K, Rb),^[29] and experimentally detected in Cd₃As₂^[40–42] and Na₃Bi.^[44,43]

As the electrons in 3D DSMs also possess linear dispersions, they have been expected to exhibit qualitatively-similar field response to graphene.^[21,45] Hence, for applications where the properties of graphene are desired in bulk materials, 3D DSMs present themselves as natural candidates.^[40,44,45] For instance, Cd₃As₂^[46–48] has been shown to perform well as saturable absorbers in the mid-IR regime^[49] owing to its strong broadband light–matter interaction,^[50,51] much like graphene. Furthermore, they can be realized as optical thin films,^[51,52] enabling the application of conventional semiconductor methods for parameter control.^[51] Recent exciting experiments have also demonstrated generation of terahertz radiation up to the 3^rd[53] and 7^th[54] harmonics, and a theoretical study predicted the generation of harmonics beyond the 31^st order with conversion efficiencies far exceeding the high-harmonic generation (HHG) in graphene by virtue of a finite interaction volume. For these reasons, 3D DSMs are attractive candidates for novel nanophotonic and nanoplasmonic applications or as viable alternatives to graphene. With increasing exploration into the potential applications of 3D DSMs, a theoretical understanding of how Dirac physics determine the linear and nonlinear optical properties is crucial. The slope of the linearly dispersing Dirac conic band structure around the nodal band touching point is commonly referred as the Fermi velocity, which serves as an important velocity-like parameter that characterizes the electronic band structure of Dirac materials. While a few works^[45,55,56] have provided a theoretical treatment for the linear optical response of a 3D Dirac dispersion, none has studied the effects of the pronounced anisotropy between the Fermi velocities along different directions – a property inherently present in 3D DSMs which have been discovered so far, on the linear optical response. As such, it is crucial to include these effects and examine if these anisotropies can be exploited for novel applications.

In this work, we derive the linear interband and intraband conductivities using the Kubo formula. We use a Hamiltonian which describes arbitrary Fermi velocity in each direction, taking us beyond previous works which were restricted to the isotropic dispersion. In obtaining our expressions for the dynamic conductivities in each direction, we find that both the intraband and interband conductivities of 3D DSMs scale as σ_ii ∝ v_i/(v_jv_k), where i,j,k∈{x,y,z}, i is the direction parallel to the incident light polarization, and j and k are the directions perpendicular to the incident light polarization. Additionally, we show that the anisotropy between the responses of the i and j directions exhibits the analytical universal scaling relation for the optical conductivity, σ_i/σ_j ∝ (v_i/v_j)².

For realistic 3D DSMs such as Cd₃As₂ and Na₃Bi, this anisotropy ratio can exceed an order of magnitude, emphasizing the importance of including anisotropy in optical calculations. More intriguingly, the optical extinction ratio reaches 15.8 and 19.2, respectively, for Cd₃As₂ and Na₃Bi, which is substantially higher than that of vast majority of anisotropic optical materials previously reported (see Table 2 below). Importantly, such optical anisotropy covers a broad terahertz (THz) window of sub-THz to at least 50 THz and is insensitive to temperature and defect scattering effects. Our findings thus reveal the nontrivial role of the anisotropic Fermi velocities on the optical response of 3D DSMs and the previously unknown potential of 3D DSM as an exceptionally strong and ultra broadband anisotropic optical material. These results shall form the harbinger for the designs of novel polarization-sensitive nanophotonic, chip-integrable plasmonic, and optoelectronic platforms for a wide array of applications such as optical switching, photodetection, energy conversion, and light modulation.

Close to the Dirac point, an electron within a 3D Dirac semimetal with momentum p = (p_x,p_y,p_z) obeys the following low-energy effective Hamiltonian:

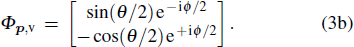
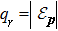
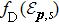
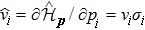
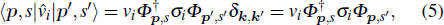
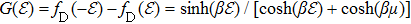
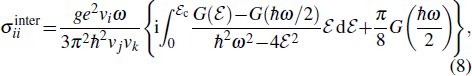
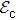
Figure 1 shows the longitudinal conductivity of two recently discovered 3D DSMs Cd₃As₂ and Na₃Bi in each Cartesian direction i ∈{x,y,z}. These 3D DSMs possess a strong Fermi velocity anisotropy between the p_x–p_y and p_z directions: v_z < v_x,v_y. Figures 1(b) and 1(e) indicate that the characteristic dependence of the optical conductivity of the 3D Dirac fermions on the frequency of the incident light, as seen in previous works,^[55] remains invariant with respect to direction. However, the difference in the magnitudes of Re(σ_ii) and Im(σ_ii) as a function of direction is drastic. The nontrivial difference in the strength of the optical response in each direction is further emphasized by the polar plots in Figs. 1(c),1(d), 1(f), and 1(g), which show the dependence of the magnitude of the conductivity^[57]

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Anisotropic optical response of 3D Dirac semiemtals. (a) Schematic depiction of a 3D Dirac cone band structure with anisotropic Fermi velocities in each momentum direction. Longitudinal conductivities of anisotropic 3D DSMs Cd3As2 (b) and Na3Bi (e) in each direction as a function of angular frequency ω. Due to the extreme anisotropy of the Fermi velocities between the in-plane (px, py) and out-of-plane (pz) directions in both 3D DSMs, σzz ≪ σxx,σyy. The polar plots in (c), (d), (f), and (g) show the directional dependence of the optical conductivity σ as a function of angles. For all cases considered here, we considered 3D DSMs doped to meV at temperature T = 4 K, a scattering time of 450 fs, and a combined spin and valley degeneracy g = 4. We consider experimentally determined values of the Fermi velocities, as listed in Table 1.

Table 1.

Table 1.

Table 1. Strong optical anisotropy of 3D Dirac semimetals Cd3As2 and Na3Bi. The optical extinction ratio Λij (i ≠ j) is defined in Eq. (10). We considered experimentally measured values of the Fermi velocities.[40,44] . Material vx/(m/s) vy/(m/s) vz/(m/s) Λxy Λyz Λxz Cd3As2 1.28 × 106 1.30 × 106 3.27 × 105 0.97 15.8 15.3 Na3Bi 4.17 × 105 3.63 × 105 0.95 × 105 1.32 14.6 19.2

Table 1. Strong optical anisotropy of 3D Dirac semimetals Cd3As2 and Na3Bi. The optical extinction ratio Λij (i ≠ j) is defined in Eq. (10). We considered experimentally measured values of the Fermi velocities.[40,44] .

We now turn our attention to the dielectric function of anisotropic DSMs. We compute the diagonal (i.e., longitudinal) elements of the dielectric tensor from the conductivity by

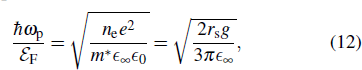
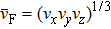
We see from Fig. 2, which shows the real part of ϵ_ii(ω) for Cd₃As₂ (a) and Na₃Bi (b), that when Re(ϵ_ii) < 0 (Re(ϵ_ii) > 1), the 3D DSMs exhibit metallic (dielectric) response, a behavior predicted^[55] in isotropically dispersing 3D DSMs. We find once again that besides a qualitatively similar response in each direction, the magnitude in each direction possesses the same v_i/v_jv_k scaling as the conductivity. As a result, the anisotropy ϵ_ii/ϵ_jj is also described by the universal scaling law given by Eq. (10). As 3D DSMs operating in the metallic regime can support the surface plasmon-polaritons (SPPs), the anisotropic dielectric function implies that the incident field polarization direction could potentially be used to tune the field confinement factor and propagation length of the SPPs. As opposed to isotropic DSMs such as graphene, this provides an additional degree of freedom for tuning the strength of light–matter interaction within 3D DSMs, which can potentially be a useful feature for plasmonic and sensing device applications.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Real part of the dielectric function ϵii(ω) in each direction for 3D DSMs Cd3As2 (a) and Na3Bi (b). The plasma frequency in each direction ωp,i corresponds to Re[ϵii(ω)] = 0, indicated by the horizontal dashes in both panels. The plots indicate the vast difference in the dielectric (Re[ϵii(ϵ)] > 1) or metallic (Re[ϵii(ω)] < 0) response of 3D DSMs between directions at a given frequency . Unless otherwise stated, we consider the same parameters as those Fig. 1}

In the above analysis, we have considered an isotropic value of ϵ_∞ which is frequently measured in experiments. We expect that the measured value of ϵ_∞ should be significantly different in each direction, the incident light polarization (with ω appropriately chosen) could tune not only parameters like the field confinement factor, but also serve as a switch between dielectric and metallic operation regimes. This arises as the zero-crossing Re(ϵ_ii) = 0 occurs at different values of ω_p,i for each direction i. Hence the anisotropy could additionally serve as a tuning parameter for the nature of light–matter interaction within 3D DSMs.

We now calculate the absorption coefficient in the i ∈ {x,y,z} Cartesian direction as^[62,63]

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Linear dichroism of 3D DSMs Cd3As2 and Na3Bi. We see from panels (a) and (b) that there is a large linear dichroism exhibited in the z-direction (black solid lines) due to the strong out-of-plane Fermi velocity anisotropy in pz. We show in panels (c) and (d) that the anisotropy of the absorption coefficient persists over a range of realistic Fermi levels. We find that the anisotropy ratio of the absorption coefficient, αi/αj ∝ vi/vj. Unless otherwise stated, we consider the same parameters as those in Figs. 1 and 2. We compute the absorption coefficient using Eq. (14). We schematically illustrate in panel (e) a possible experimental geometry which could potentially enable the detection of the strong optical anisotropy of 3D DSM thin films. By changing the polarization of a linearly polarized laser normally incident on the x–z plane of the 3D DSM thin film (since vx exceeds vz by a significant amount), the strength of the transmitted field detected will change.

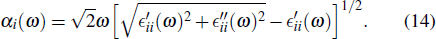
We have shown, using the Kubo–Greenwood formula, that when the anisotropic Fermi velocities in each direction are included, the optical response along each direction varies significantly. While the characteristic optical signatures of 3D Dirac electrons like the σ(ω) ∝ ω scaling are retained, our results show that the magnitude along each direction scales as v_i/(v_jv_k). This leads to the following universal scaling of the optical anisotropy ratio between the i and j directions: σ_ii/σ_jj = ϵ_ii/ϵ_jj = (v_i/v_j)² – a value which exceeds 15 times for Cd₃As₂ and 19 times for Na₃Bi, as shown in Table 1. While we find that the qualitative trend of ϵ_ii(ω) remains the same in all directions, the large anisotropy implies that for plasmonic applications, the polarization of the incident light can serve as an additional degree of freedom with which the field confinement factor and propagation length of SPPs can be tuned. In the case where ϵ_∞ is different in each direction, the plasma frequency ω_p will acquire a directional dependence. This implies that at an appropriately chosen frequency, dielectric (e.g., waveguide modes) or metallic (SPPs) behavior can dominate depending on the direction of the incident light, thus opening up a novel device architecture where both the strength and the nature of light–matter interaction could be tailored using the incident light polarization. We further note that the linear dichroism of 3D DSMs with Fermi velocities anisotropy is substantially stronger than that of many anisotropic optical materials as shown in Table 2.^[62,64–73] Although the extinction ratio is dwarfed by other exceptionally strong anisotropic optical materials, such as bilayer tellurene,^[73] and antimonene, the broadband linear dichroism of Cd₃As₂ and Na₃Bi represents a unique strength not found in bilayer tellurene and antimonene.

Table 2.

Table 2.

Table 2. Comparison of the extinction ratios of different anisotropic optical materials.[62,64–74] . Material Extinction ratio Wavelength Reference Cd3As2 15.8 broadband this work Na3Bi 19.2 broadband this work PbS nanowire 2.38 532 nm [64] Black phosphorus 5 1557 nm [65] Sb2Se3 16 633 nm [66] AuSe 3 450 nm [67] (iBA)2(MA)Pb2I7 1.23 637 nm [62] 1D C4N2H14PbI4 5.5 405 nm [68] GeSe monolayer 3.4 450 nm [69] GeSe nanoflakes 3.02 808 nm [71] ReS2 3.5 532 nm [70] Bilayer tellurene 2812 365 nm [72] Antimonene 145 387 nm [73]

Table 2. Comparison of the extinction ratios of different anisotropic optical materials.[62,64–74] .

In summary, we studied the linear optical response of topological Dirac semimetal. We found that the optical conductivity exhibits strong anisotropy with the universal scaling law, Λ_ij = (v_i/v_j)², independent of temperature, Fermi level, and scattering effects, and is broadly applicable to the sub-THZ to at least 50 THz frequency window. Recently, the optical properties of topological semimetals with nodal topology beyond Dirac semimetal, such as Weyl semimetal^[74] and nodal loop semimetal,^[75–78] have been extensively studied. We expect this ever-expanding family of topological semimetals,^[79] in which the optical and electronic properties are highly anisotropic along different crystal directions, to continually offer interesting platforms for the uncovering of exotic anisotropic optics and optoelectronic phenomena critical for the design of next-generation novel devices.