† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11564024, 51731001, and 11574122) and the Fundamental Research Funds for the Central Universities, China (Grant No. lzujbky-2019-kb06).
We establish a theoretical bimodal model for the complex permeability of flaky soft magnetic composite materials to explain the variability of their initial permeability. The new model is motivated by finding the two natural resonance peaks to be inconsistent with the combination of the domain wall resonance and the natural resonance. In the derivation of the model, two relationships are explored: the first one is the relationship between the number of magnetic domains and the permeability, and the second one is the relationship between the natural resonance and the domain wall resonance. This reveals that the ball milling causes the number of magnetic domains to increase and the maximum initial permeability to exist after 10 h of ball milling. An experiment is conducted to demonstrate the reliability of the proposed model. The experimental results are in good agreement with the theoretical calculations. This new model is of great significance for studying the mechanism and applications of the resonance loss for soft magnetic composite materials in high frequency fields.
Soft magnetic materials are widely used in today’s society,[1–3] such as in the areas of inductors, transformers, and electrical machines. These materials are widely applied due to their complex configurations (conductive magnetic particles in an insulating matrix), large resistivity, low energy loss during magnetic circuit cycling, and excellent performance.[5,6] However, these electronic devices need to operate at higher operating frequencies with less loss to meet the requirements of both current and future applications. Therefore, improving the working frequency andreducing the loss of electronic devices have become an urgent problem to be solved.[4] To this end, we start with the resonance mechanism (a type of loss mode) to derive a solution that overcomes the Snoek limit in order to increase the permeability while increasing the operating frequency.[7]
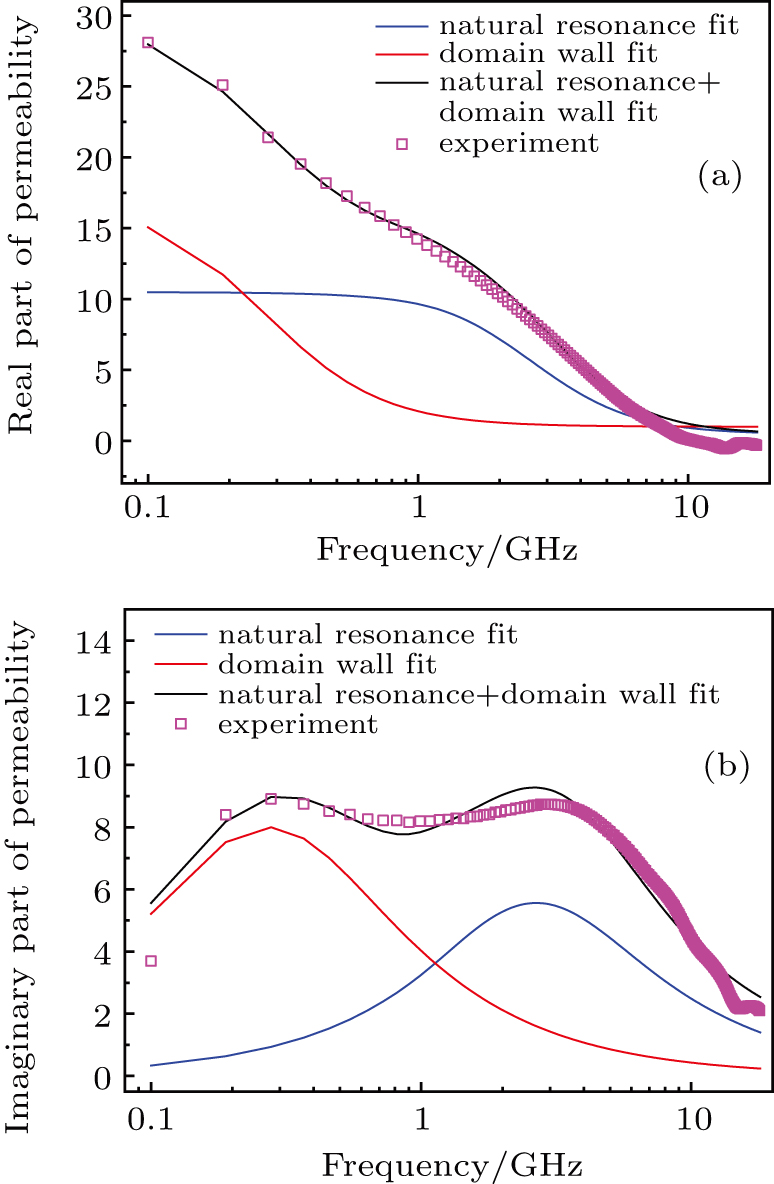
Resonance, whether domain wall resonance or natural resonance, is a loss mode of magnetic materials, and natural resonance usually determines the operating frequency of electronic devices.[8–10] Therefore, the loss mechanism for resonance has attracted widespread attention. Usually, we use the imaginary part of the complex permeability to study this loss mechanism. It consists of two completely different mechanisms: domain wall resonance and natural resonance.[11–15] In the study by Tsutaoka, these two mechanisms were used to explain the unimodal structure.[16] Dosoudil et al. have extended the research of Tsutaoka by combining the two mechanisms to carry out the unimodal structure in the fitting.[17] Hank and Deng have found that there are two peaks in the imaginary part of the complex permeability. In the high frequency range, the first peak is the domain wall resonance peak, and the second one is the natural resonance peak.[18] Although the study of the two mechanisms has made significant progress, there are few reports on the relationship between the two mechanisms and how to make the domain wall resonance peak appear. This is because the domain walls themselves are insensitive, and the natural resonance peaks obscure the domain wall resonance peaks, making them difficult to identify. Only in the presence of a large number of domain walls, are the domain wall resonance peaks revealed and separated from natural resonance (as shown in Fig.
In this paper, the ball milling method is used. This method flattens the spherical particles, greatly improves the magnetic permeability while obtaining a large number of magnetic domains, and separates the domain wall resonance peaks from the natural resonance peaks. Then, the two mechanisms are combined to establish a new model, and the relationship between the two mechanisms is studied and discussed. The relationship between the number of domain walls and the domain wall resonance, in addition to the relationship between the number of domain walls and the initial permeability is verified in a ball milling experiment. The experimental results are consistent with the computed results based on the model. According to the model established by the two mechanisms, the curve of the bimodal structure is also well fitted, which is a good illustration of the rationality of the model. The analysis and discussion of the relationship between the two mechanisms is presented. The proposed model provides a new way to study the high frequency loss of soft magnetic composite materials. It is also beneficial to improving the magnetic permeability and increasing the operating frequencies of soft magnetic composite materials and their related devices (inductors, transformers, and electrical machines).[20]
As shown in Fig.
Carbonyl iron particles used in the experiment are MCIP-5 carbonyl iron particles produced by Shanxi Xinghua company, and their particle size is 5 μm–6 μm. First, the powder is ground in the planetary ball mill. We use two ZrO grinding balls, respectively, with a radius of 5 mm and 3 mm. The large and small balls are mixed in the 1 : 1 mass ratio and put into a ball mill. The large ball can crush the spherical carbonyl iron particles well, and can effectively turn the spherical particles into flaky particles, and the small balls further thin the flaky particles. The ball-material ratio is 20 : 1, and the ball grinding medium is alcohol. The speed is set to be 400 r/min, and the time of ball-milling is gradually extended. The ball-milling samples were obtained with ball milling times of 4 h, 6 h, 8 h, 9 h, 10 h, 11 h, and 12 h, respectively. The scanning electron microscope (SEM) (Apreo S) is used to measure the morphology and structure of the ball-milling samples.
We prepared a ball-milled carbonyl iron powder into a polyurethane-based composite with a volume fraction of 55%. The goal was to study the loss of the core at high frequencies, so the volume fraction was set to be as high as possible, which induced the phenomenon of falling powder. The corresponding amount of polyurethane was added to acetone and ultrasonically treated for 10 min to dissolve it; then, 0.5-g carbonyl iron particles were added into the resulting mixture. To ensure that the carbonyl iron particles and the polyurethane were fully mixed, we stirred them for 30 min ultrasonically, which also facilitated evaporating the acetone and drying the sample. The mixture was put into an annular mold which has an outer diameter of 7 mm and an inner diameter of 3.04 mm. The mixture was pressed into a ring-shaped sample with a thickness of 0.6 mm–0.8 mm at a pressure of 4 MPa. The composite permeability of the sample in a range of 0.1 GHz–18 GHz was measured by using a vector network analyzer (Agilent E8363B).
The ball milling at 400 r/min flattened the original spherical particles. As a result, the thickness of the flaky particles gradually decreased as the ball milling time increased, and the diameter gradually increased as shown in Fig.
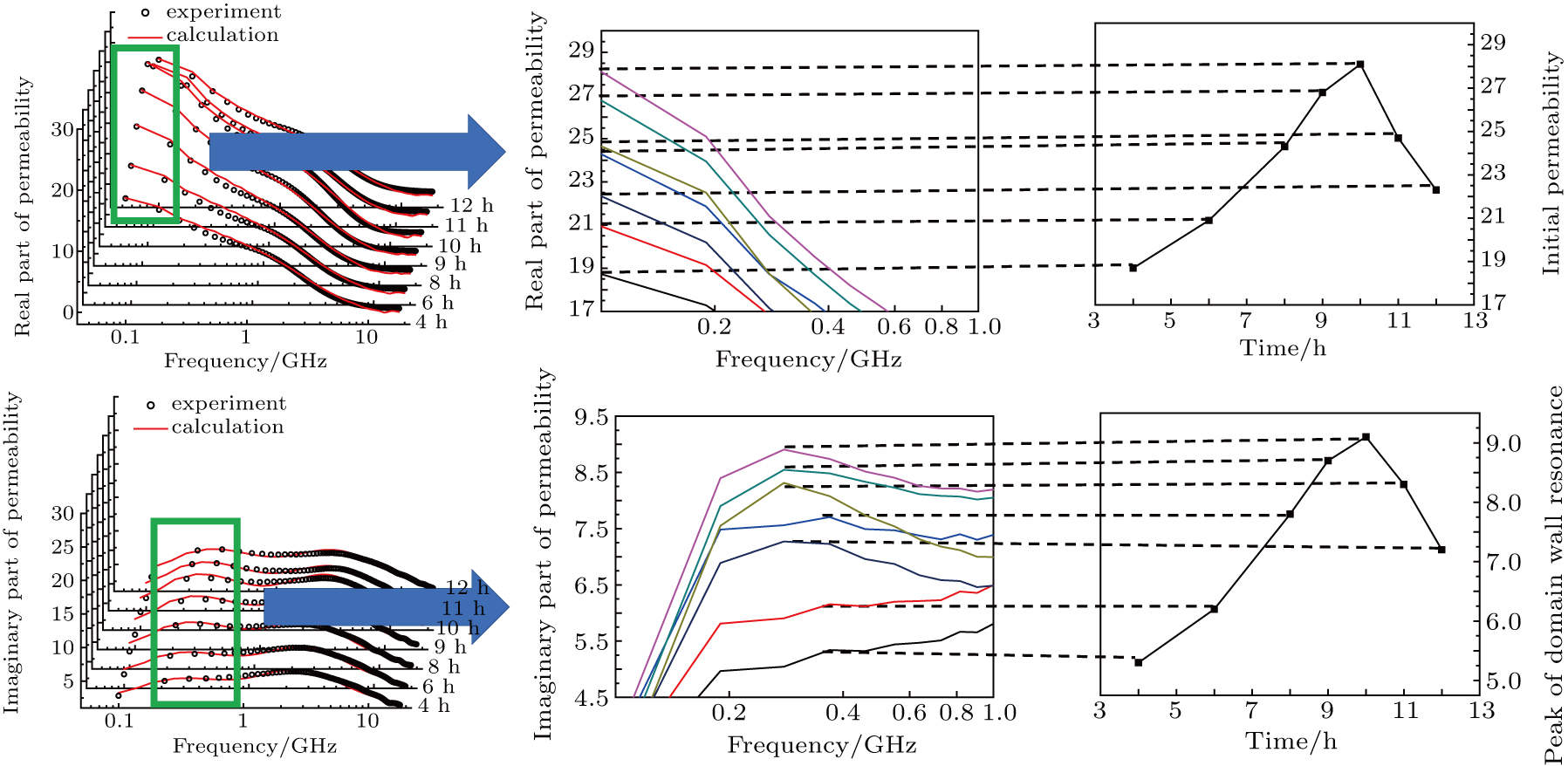
As the ball milling time is extended, the thickness of the flaky particles gradually decreases. Initially, the diameter increases and subsequently decreases. This is because the ball grinding time is excessive, during which the original larger flake particles are broken into smaller flake particles. This lead the diameter-thickness ratio to first increase and then decrease. This change in the ratio affects the permeability: the permeability also initially increases and then decreases (as shown in Fig.
This variation in the diameter-thickness ratio also affects the change in the number of magnetic domains. This number is related to the decreasing in thickness of the flaky particles over time. The width D of the magnetic domains is proportional to the thickness l of the sample particles. In our study, the thickness reduction caused by ball milling is far from the critical value reached when a single domain structure forms. For a spherical ferromagnetic particle, the critical radius of single domain for carbonyl iron is 2 nm; for a flaky particle with a thickness of 600 nm, the critical width of single domain for carbonyl iron is approximately 45 nm, both values are much smaller than the size of our balling milling particles.[22]
As the thickness l decreases, the number of magnetic domains per unit volume increases.[23] In the early stage of the ball milling process, the number of magnetic domains increases as the thickness decreases. Over time, the number of domain walls increases with the number of magnetic domains increasing. When large flaky particles break from prolonged and excessive ball milling, the thickness of the flaky particles continues to thin, but its diameter can also be significantly reduced. As a result, there is an increase in the number of magnetic domains per unit volume. However, the total volume decreases as the diameter decreases, and the number of magnetic domains begins to decrease as shown in Fig.
In summary, the ball milling process causes the aspect ratio of the flaky particles to change. This changes the number of magnetic domains and domain walls, thereby affecting the variation of the domain wall resonance peaks and the magnetic permeability.
The model is established by combining the two mechanisms of domain wall resonance and natural resonance. On the one hand, the permeability affected by the natural resonance mechanism is partly calculated according to the LLG equation, and we consider the spatial random distribution of the easy magnetization axis. Since the sample is made from a carbonyl iron compound embedded in polyurethane, we calculate the effective permeability through the effective medium theory.[24] On the other hand, the permeability affected by the domain wall resonance is calculated according to the domain wall motion equation. The complex permeability of the sample is obtained by combining the two. Although we do not take into consideration the influence of the skin effect in the proposed model, the theoretical calculation results and experimental results have confirmed the model’s reliability.
In the absence of an external magnetic field, the distribution of magnetization intensity is always in the direction of the lowest energy due to the magnetic anisotropic energy. Therefore, we can use the equivalent anisotropic field Hk to replace the influence of magnetic anisotropic energy. We can use the LLG equation to calculate the effective permeability

Since the magnetic field lags behind the external magnetic field in the alternating electromagnetic field and thus produces a phase difference, we can use the permeability in the complex form as follows:


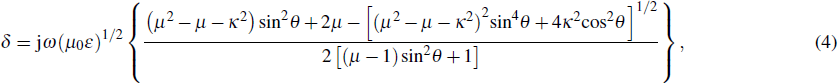

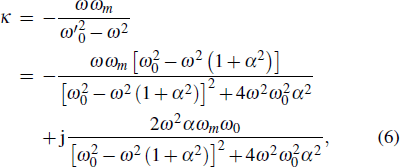

In this process, we introduce the permeability tensor. We take the spatial orientation of the magnetic moment into consideration. This makes the damping factor α less than one, which is more in line with the physical meaning. If we use the LLG equation directly in the model, the damping factor α may be greater than one.
Since the distribution directions of the easy magnetic axes are random, we choose 104 single domains, and each domain can produce the intrinsic permeability at random angles (θ and ϕ)[27] as follows:

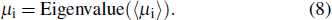
We can obtain the domain wall motion equation which is based on the properties of the domain wall that Doring proposed.[28] Using Eq. (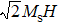
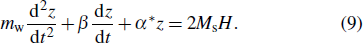
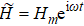
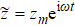
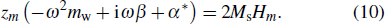



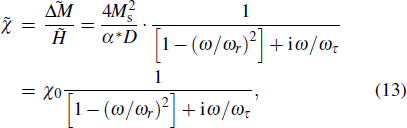



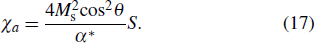
We obtain the permeability of the domain wall μw from the following equation:


The flake magnetic powder particles are dispersed in the insulating matrix. In the composite system, in order to obtain its effective permeability, Bruggeman’s effective medium theory can be used as follows (a correction parameter included):[31]


The two mechanisms have different contributions in the imaginary part of the magnetic permeability. The contribution of the domain wall resonance is mainly in the MHz band, and the natural resonance mainly contributes to the GHz band (as shown in Fig.
The sample milled by balls for 10 h is taken for example. Under the joint action of the two mechanisms, the experimental results are basically consistent with the theoretical results, which proves the reliability of our model.
According to the fitting process and the results, it is found that the natural resonance and the domain wall resonance are controlled by two different mechanisms. In addition, there are five parameters in the fitting process: the equivalent anisotropic field Hk, the damping factor α, the static magnetic susceptibility χ0, the circular frequency of eigenvibration of the domain wall ωr, and the circular frequency of relaxation frequency ωτ, which are illustrated in Fig.
The model is mainly divided into two parts: the domain wall resonance and the natural resonance. In the domain wall resonance part, χ0, ωr, and ωτ are the main parameters, whereas Hk and α are the main parameters in the natural resonance part. This indicates that the five parameters are not independent of each other, and their relationships are explored below.
According to the fitting results, both Hk and χ0 are the main factors affecting the imaginary part of the magnetic permeability, Hk and χ0 have completely opposite trends, and both Hk and χ0 are affected by a common factor, the magnetocrystalline anisotropy constant K. The equivalent anisotropic field Hk and the magnetocrystalline anisotropy constant K have the same variation trend. From the fitting results, we find that Hk first decreases and subsequently increases (as shown in Fig.
The fitting result of the static magnetic susceptibility χ0 is completely opposite to the equivalent anisotropic field Hk, which is also caused by the magnetocrystalline anisotropy constant K. We can learn from Eq. (

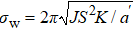
By Eq. (
The Hk and χ0 are the two main controlling parameters of the natural resonance and the domain wall resonance, respectively. They are both affected by K. As K initially decreases and then increases, the parameters respond as follows: Hk first decreases and then increases; χ0 first increases and then decreases (K affects χ0 through influencing α*).
The damping factor α (α = 4π μ0λ/γ Ms) varies proportionally with the relaxation frequency λ. According to Fig.
We bring the damping factor of the domain wall β (β = π μ0λ σw/λ2A) into Eq. (

The circular frequency of eigenvibration of the domain wall ωr is determined jointly by mw and α*, which are expressed as


Substituting Eqs. (

From the fitting results we obtain that the circular frequency of eigenvibration of the domain wall ωr is much larger than the circular frequency of the relaxation frequency ωτ as shown in Fig.
The five parameters involved in the fit are not independent of each other. Among them, Hk and χ0 are controlled by K, α and ωτ are controlled by λ, and ωr is basically constant. The domain wall resonance and the natural resonance are related by K and λ, thereby linking the two mechanisms together. By fitting the results, the experimental data and the fitting results are basically coincident as shown in Fig.
From the magnetic spectrum, we find obvious changes in the domain wall resonance peaks. This is due to the increase in the number of domain walls,[19] which causes the domain wall resonance peaks to separate from the natural resonance peaks. As the number of domain walls first increases and then decreases, the intensity of the domain wall resonance peaks correspondingly changes (i.e., first increases and decreases). This is the same as the change in the initial permeability. In the domain wall resonance mechanism, χ0 is the main factor controlling the intensity of the domain wall resonance peak, and its change trend is the same as those of the peak strength and initial permeability of the domain wall resonance peak. The variation in the number of magnetic domains and domain walls lead to a certain change in χ0. In Eq. (
In the ball milling process, the increase in the number of magnetic domains and domain walls caused by the flattening not only cause the separation of the domain wall resonance peaks and the natural resonance peaks, but also contribute to an increase in the magnetic permeability. The enhancement of the domain wall resonance peak and the increase of the initial magnetic permeability clearly embody this result. Furthermore, the initial decrease then subsequent increase of Hk, as well as the initial increase then decrease of χ0 in the fitting parameters also verify this result and confirm the reliability of the model.
In our experimental study, we improved the permeability of carbonyl iron in ball milling by changing the particle morphology and improving the width-and-thickness ratio of the sample. The preparation of flaky carbonyl iron can be completed by ball milling alone. Therefore, the efficiency is very high, but for different ball mills there need different ball-to-material ratios and size-to-ball ratios. In the process of ball grinding, the deepening of the flattening process not only increases not only the magnetic permeability, but also the magnetic domains and domain walls. The increase in the number of magnetic domains and domain walls both further contribute to magnetic permeability. However, when excessive ball grinding occurs, the originally large and thin flake particles are broken into small and thin fragments, the diameter-thickness ratio decreases, the magnetic permeability decreases, and the number of magnetic domains and domain walls both also decrease. Therefore, the identification of the optimal ball milling time is essential.
We also established a new model with a bimodal structure (two mechanisms). In the model we consider the spatial random distribution, and then we obtain the permeability μ′ = μi + μw + 1. We also consider the influence of effective medium theory, and constrain the damping coefficient values to be less than one. If the damping coefficient exceeds one, the magnetic moment is ahead of the microwave field, which is not consistent with physical scenarios. Only when the damping coefficient is less than one, does the magnetic moment lag behind the microwave field and the precessional motion.
By relating the variation of the domain width with the variation of the domain number in the unit volume, several factors affecting the domain wall resonance are discussed. It is found that the domain wall resonance is related to not only the number of domain walls, but also the magnetocrystalline anisotropy constant K and the relaxation frequency λ. Among the five fitting parameters, Hk and χ0 are affected by K, whereas α and ωτ are affected by λ. In this way, both the domain wall resonance and the natural resonance are jointly controlled by K and λ. Thus we can relate the domain wall resonance to the natural resonance by studying K and λ.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |