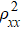† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11774007 and U1832214), the National Key R&D Program of China (Grant No. 2018YFA0305601), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB28000000).
We grew single crystals of vanadium-substituted, ferromagnetic Weyl semimetal candidate Zr1−xVxCo1.6Sn from molten tin flux. These solid solutions all crystallize in a full Heusler structure (L21) while their Curie temperatures and magnetic moments are enhanced by V-substitution. Their resistivity gradually changes from bad-metal-like to semiconductor-like with increasing x while the anomalous Hall effect (AHE), which can be well fitted by Tian–Ye–Jin (TYJ) scaling,[1] is also enhanced. Moreover, we find an apparent electron–electron interaction (EEI) induced quantum correction in resistivity at low temperature. The anomalous Hall conductivity (AHC) dominated by the intrinsic term is not corrected.
Discovery of Weyl semimetal has motivated the interest for investigating topological electronic structure and related transport properties of various semimetal materials.[2,3] Of particular interest is ferromagnetic (FM) semimetal in which the breaking of time reversal symmetry can generate large Berry-curvature-bearing Weyl nodes and strong intrinsic anomalous Hall effect (AHE) thereupon.[4] Very recently, the existence of Weyl quasi-particles and topological nontrivial surface states has been observed in FM semimetals Co3Sn2S2 and Co2MnGa in spectroscopic experiments.[5–7] These magnetic Weyl semimetals manifest a large, intrinsic AHE which is also believed to be a signature of the existence of topological Weyl nodes.[5,8] Understanding the mechanism of AHE and its correlation to the topological nontrivial band structure is crucial for the material design aiming for future electronic devices working based on the anomalous effect.
Heusler compounds represent a large family of materials crystallizing in closely related structures and many of them have been considered as the candidates of magnetic Weyl semimetal.[9,10] These candidates include half-Heusler GdPtBi and full-Heusler Co2MnGa,[5,11] both of which exhibit large AHE. The Co-based full Heusler compounds have attracted much attention because they own some advantages such as strong magnetism and tunability which may promise their future applications in electronic devices. Their magnetic ground state is controlled by the interatomic distance and follows the well-known Slater–Pauling rule,12-14 leading to a relatively high Curie temperature (TC). Moreover, changing their crystalline symmetry can tune the AHE from null to very large while keeping the magnetization the same.[15] When the number of the valence electrons equals 26, the Co-based full Heusler compounds manifest a particular half-metallic Weyl semimetal state, i.e., the spin-up electron bands form a topological nodal line and Weyl nodes while the spin-down electron bands possess a fully opened gap.[15–17] These 26 e compounds include ZrCo2Sn, TiCo2Sn, and VCo2Ga, whose electronic structures have been well calculated.[16–18]
In this paper, we exam the magnetic and electric transport properties of single-crystalline vanadium-substituted ZrCo1.6Sn. Previous studies on the poly-crystalline parents compounds, ZrCo2Sn and VCo2Sn, reported their FM ground state.[19–22] Recent electronic structure calculations unveiled a pair of Weyl nodes 0.6 eV above the Fermi level for ZrCo2Sn.[16] Moreover, the calculation also suggested that 10% of V-substitution on TiCo2Sn and 30% of Nb-substitution on ZrCo2Sn will shift the Fermi level to the Weyl nodes energy while keeping the main band topology unchanged.[16] However the AHE of the pristine and Nb-substituted ZrCo2Sn has not been analyzed thoroughly, although the single crystal growth, magnetic and electric transport properties have been reported.[23–25]
Realizing the difficulty for growing single-crystalline TiCo2Sn,[26,27] we successfully grew single crystals of Zr1−xVxCo1.6Sn with the L21 Heusler phase structure from molten tin flux. We found that their Curie temperature and magnetic moment are enhanced by V-substitution while the resistivity changes from bad-metal-like to semiconductor-like at x = 0.35. Their AHE, which can be well fitted by Tian–Ye–Jin (TYJ) scaling,[1] is also enhanced by V-substitution. Moreover, we find an apparent electron–electron-interaction (EEI) induced quantum correction in longitudinal resistivity at low temperature. On the other hand, the AHE, which is dominated by the intrinsic term, is not corrected.
Single crystals of Zr1−xVxCo1.6Sn were grown in tin-flux with zirconium powder (99.8 %, Alfa Aesar), vanadium dendritic crystals (99.9 %, GRINM), cobalt powder (99.8 %, Alfa Aesar), and tin lumps (99.99 %, GRINM) as starting materials with the molar Zr : V : Co : Sn ratio of (1−x) : x : 2 : 19. The mixture was placed in an alumina crucible and then sealed in a fused silica ampoule with 0.02 MPa argon gas. The ampoule was slowly heated to 1100 °C in furnace and kept at this temperature for 12 h, followed by a slow cooling to 1000 °C at a rate of 2 °C/h. At this temperature, large single crystals were separated from molten tin by centrifugal decanting. Every single crystal for electrical and magnetic measurement was polished. The thickness is about 0.1 mm or less and no residual tin was visible. With increasing V substitution, the crystals’ shape evolves from a truncated octahedron to a well-faceted cube displaying large (100) faces [insets in Fig.
Power x-ray diffraction (Cu-Kα) measurements were conducted at room temperature with a Rigaku MiniFlex 600 diffractometer to confirm the crystal structure. The compositions of Zr, V, and Co for the series were determined by energy dispersive x-ray spectroscopy (EDS) in an X-Max 80. DC magnetization was measured by a Quantum Design superconducting quantum interference device magnetometer in a variety of applied fields (μ0H ≤ 6 T) and temperatures (T = 2–300 K). The samples were mounted and fixed by GE varnish on a brass stick, with fields perpendicular to the face of (100). AC electrical resistivity measurements were performed in a Quantum Design physical property measurement system (T = 2–300 K, −9 T≤ μ0H ≤ 9 T). A standard four-wire method was adopted using silver paste as the contacts. The resistivity and Hall effect measurements were conducted with fields normal to and currents within the (100) plane.
Figure 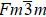
Figures
Figure
Figure
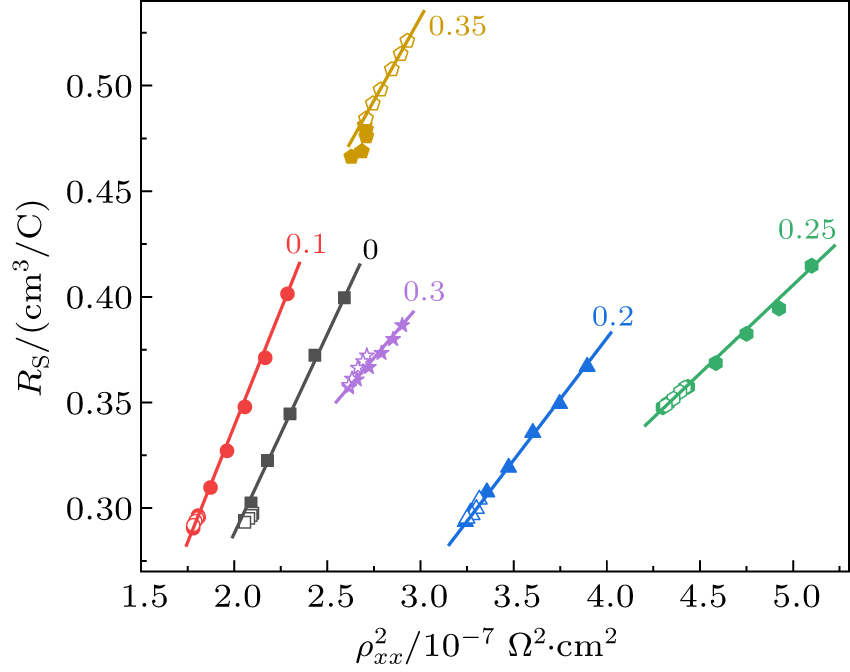
Empirically, ρyx comprises two terms[28]

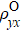
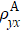
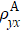
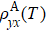
In order to shed light on the mechanisms of AHE, the experimental data are fitted with the scaling laws in which the influence of M(T) is also taken into account.[29–32] We find that the data can be well fitted by a modified TYJ scaling[1,33,34]
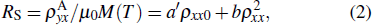
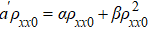
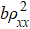
Figure 
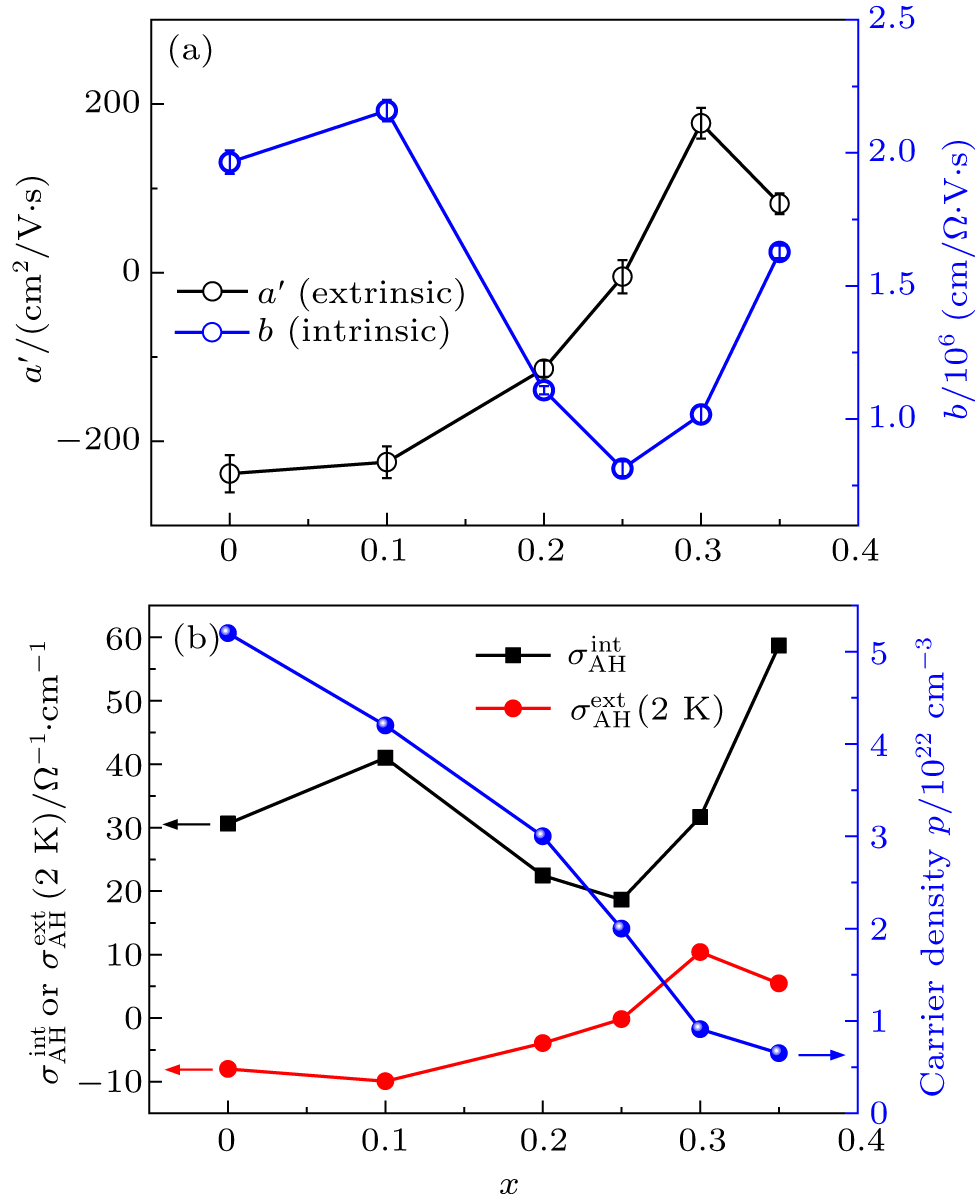
The fitting coefficients a′ and b, representing the extrinsic and intrinsic contributions, respectively, are plotted against x in Fig. 

We firstly discuss the crystalline and magnetic properties of Zr1−xVxCo1.6Sn. As reported by Kushwaha et al.,[23] the tin-flux grown ZrCo2Sn crystals inevitably have Co vacancies which significantly suppress the TC and μsat. The Co vacancies also affect the density of states of the minority spins in electronic structure.[35] Our measurements reveal that the properties of pristine ZrCo1.6Sn are close to those reported by Kushwaha et al.[23] and the whole series show the same Co vacancies. We also notice that the lattice parameters in polycrystalline ZrCo2Sn (6.25 Å) and VCo2Sn (5.98 Å) differ in 0.27 Å,[21] which is approximately triple the change of a from x = 0 to 0.35. This linear change of a is consistent with our EDS measurements and verifies that Co vacancies are unchanged for different x.
Previous study showed that polycrystalline VCo2Sn has TC = 105 K and μsat = 1.2 μB/F.U.[21] and therefore a naive expectation is that the magnetism will be suppressed by V-substitution in ZrCo1.6Sn. In contrast, we observed that the TC and μsat slightly increase until x = 0.35 in Zr1−xVxCo1.6Sn, which conforms to the well-know Slater–Pauling rule[36] but contradicts the expectation. Please note this TC change is also distinguished from the case of Zr1−xNbxCo2Sn[25] in which the Nb substitution leads to the weakening of ferromagnetism. This unexpected change of magnetization in our case is consistent with the previous studies on Co2Ti1−xVxSn[37,38] in which the saturation magnetization initially increases with x until x = 0.4 and then drops. We speculate that it may be related to the chemical pressure difference while the 3d characteristics of V atoms may also play a role. Further elaboration on the whole series from x = 0 to 1 is needed for understanding this puzzle.
As theoretically predicted,[16] ZrCo2Sn has stable Weyl nodes located slightly above the Fermi level which can be tuned by alloying 30 % Nb. Although the Co vacancies strongly modify the magnetic properties, the Weyl nodes should not be annihilated by the disorder as they are protected by the crystalline symmetry.[23] In Zr1−xVxCo1.6Sn we observed an enhanced intrinsic AHE which may be correlated with Weyl nodes energy approaching to the Fermi level. According to the previous calculation,[18] VCo2Sn is not a half metal and it has an AHC as large as −1500 Ω−1⋅cm−1. However we do not observe a transition from positive to negative in the AHE for Zr1−xVxCo1.6Sn till x = 0.35. As shown in Fig.
In the last part, we clarify the low-temperature upturn in resistivity in Fig.

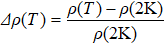
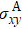
It is well-known that the WL contributes to the extrinsic AHC[40,44] while the EEI will not lead to any correction to the AHC.[29,45,46] However recent experiment observed a large correction to the AHC originating from EEI in HgCr2Se4.[39] In contract, our measurements on Zr1−xVxCo1.6Sn show no correction to the AHC by EEI. Further study on various systems is needed for elaborating the relation between the quantum corrections and AHE.
In summary, we measured the magnetic and transport properties for FM Weyl semimetal candidate Zr1−xVxCo1.6Sn at x ≤ 0.35. Their AHE can be well-fitted by the TYJ scaling law which yields a dominated intrinsic term. The intrinsic AHC is slightly enhanced by increasing x. It will be interesting to investigate the solid solutions with more V-substitution but different crystal growth technique is needed.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] |