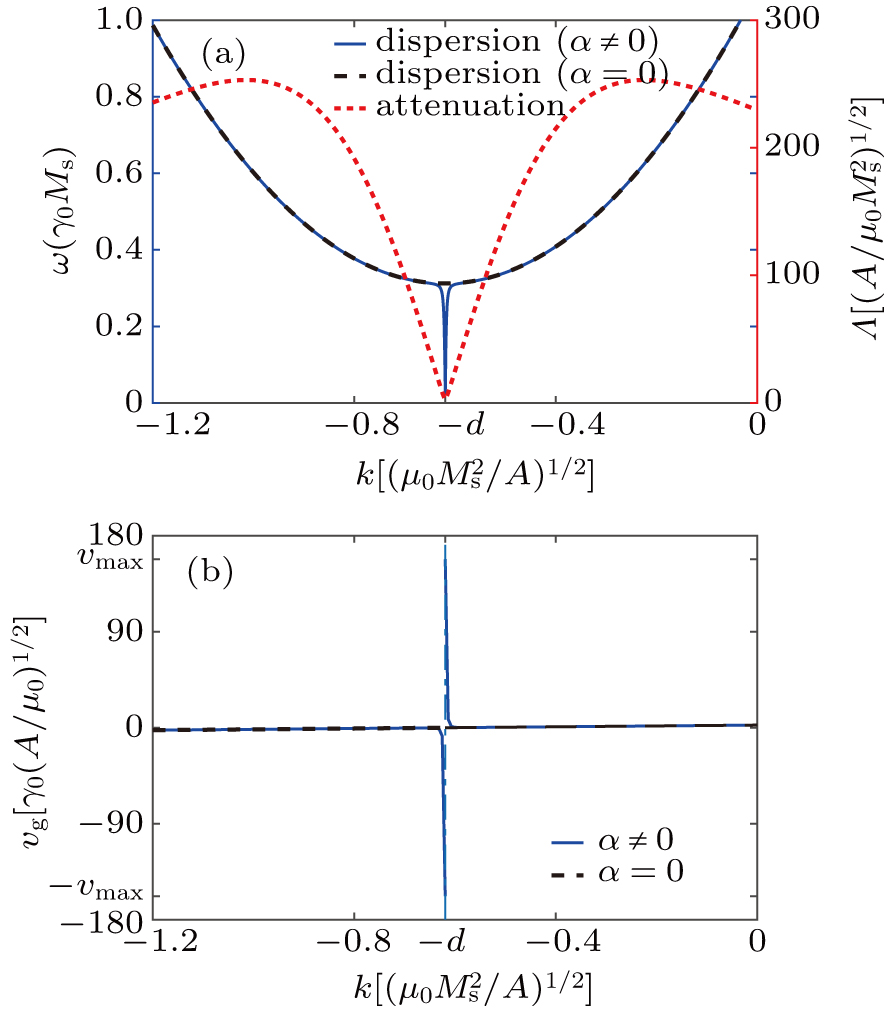
(a) Dispersion and attenuation of the spin wave excited on top of uniform configuration (θ₀ = 0). The solid curve represents the dispersion relation with damping, while the dashed curve without damping. The dotted curve denotes the attenuation length as a function of wave number. (b) Group velocity. The solid and dashed curves correspond to the cases with and without damping, respectively. Here we take typical magnetic parameters: the Gilbert damping α = 0.01, the exchange constant A = 8.78 × 10^–12 J/m, the saturation magnetization M_s = 3.84 × 10⁵ A/m, the anisotropy constant K = 10⁵ J/m³, the DMI constant D = 1.58 × 10^–3 J/m². From these parameters, the dimensionless anisotropy and DMI constants are κ=K/(μ0Ms2)=0.54 and d=D/(2Aμ0Ms2)=0.62 . The natural units of frequency, velocity and wave number are γ₀ M_s = 8.49 7#x00D7; 10¹⁰ Hz, γ0A/μ0=584 m/s and μ0Ms2/A=1.45×108 m⁻¹.