† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11888101, 91421107, and 11574004) and the National Key Research and Development Program of China (Grant Nos. 2016YFA0301003 and 2018YFA0305602).
Nematic phase intertwines closely with high-Tc superconductivity in iron-based superconductors. Its mechanism, which is closely related to the pairing mechanism of superconductivity, still remains controversial. Comprehensive characterization of the electronic state reconstruction in the nematic phase is thus crucial. However, most experiments focus only on the reconstruction of band dispersions. Another important characteristic of electronic state, the spectral weight, has not been studied in details so far. Here, we studied the spectral weight transfer in the nematic phase of FeSe0.9S0.1 using angle-resolved photoemission spectroscopy and in-situ detwinning technique. There are two elliptical electron pockets overlapping with each other orthogonally at the Brillouin zone corner. We found that, upon cooling, one electron pocket loses spectral weight and fades away, while the other electron pocket gains spectral weight and becomes pronounced. Our results show that the symmetry breaking of the electronic state is manifested by not only the anisotropic band dispersion but also the band-selective modulation of the spectral weight. Our observation completes our understanding of the nematic electronic state, and put strong constraints on the theoretical models. It further provides crucial clues to understand the gap anisotropy and orbital-selective pairing in iron-selenide superconductors.
Nematic phase, which is translationally invariant but breaks rotational symmetry, attracts great interests recently due to its close intertwining with superconductivity in iron-based superconductors (FeSCs).[1–4] The superconducting transition temperature (Tc) reaches optimal when the nematic transition temperature (Tnem) is suppressed by either chemical doping or pressure. It is therefore important to understand the underlying mechanism of the nematic phase, whose origin is closely related to the pairing interaction of high-Tc superconductivity. Theoretically, on one hand, the nematic phase could be driven by a dxz/dyz ferro-orbital ordering. The occupation difference between the dxz and dyz orbitals breaks the C4 rotational symmetry.[5–7] More complex orbital orderings have also been proposed.[8,9] On the other hand, the spin fluctuation could break the C4 rotational symmetry spontaneously, resulting in a spin-nematic phase. It drives the nematic phase transition through a coupling among spin, charge, and lattice degrees of freedom.[10,11]
To understand the mechanism of the nematic phase, it is important to characterize experimentally how the electronic state reconstructs in the nematic phase. Angle-resolved photoemission spectroscopy (ARPES) is a powerful technique that can probe the electronic structure of materials in momentum space. Band dispersions and spectral weight distributions of the electronic state can be obtained. For the nematic phase, the reconstruction of the band dispersions has been intensively studied by ARPES.[12–16] Orbital-dependent energy shifts of bands and anisotropic band dispersions have been observed. However, another important characteristic of the electronic state, the spectral weight, has not been studied in details so far. It is not clear how the spectral weights of the bands evolve with temperature and whether the spectral weight distribution breaks the rotational symmetry or not in the nematic phase.
FeSe is an ideal system to study the nematic phase.[17] The Tnem of FeSe is 90 K and there is no long-range magnetic order at low temperature. Moreover, the Tnem can be further suppressed by the sulfur substitution in FeSe1 – xSx.[18] With lower transition temperature, the thermal broadening effect can be suppressed and the detailed evolution of electronic state across the phase transition can be obtained. Here, we studied the electronic structure reconstruction in the nematic phase of FeSe0.9S0.1 using ARPES. We found that, the nematic phase transition not only results in an anisotropic band dispersion, but also leads to a band-selective spectral weight transfer on the electron pockets at the Brillouin zone corner (M). Upon cooling, one electron pocket loses spectral weight and eventually fades away, while the other electron pocket gains spectral weight. Such spectral weight transfer breaks the C4 rotational symmetry of the Fermi surface, leaving only one anisotropic electron pocket at the M point at the lowest temperature. Our results complete our understanding of the electronic structure reconstruction in the nematic phase, and put strong constrains on the theoretical models. It further provides insights into the orbital-selective pairing of iron-selenide superconductors.
High quality FeSe0.9S0.1 samples were grown using the chemical vapor transport (CVT) method.[18] The Tnem was confirmed to be ∼ 75 K according to the resistivity and magnetic susceptibility measurements. ARPES measurements were performed using a DA30L analyzer and a helium discharging lamp. The photon energy was 21.2 eV. The overall energy resolution was ∼ 10 meV and the angular resolution was ∼ 0.3°. All the samples were cleaved and measured in ultrahigh vacuum with a base pressure better than 6× 10−11 mbar. To obtain photoemission signals from one single domain, piezoelectric (PZT) stacks were used to detwin the sample in-situ.[19,20] No sample deformation was observed during the sample detwinning process. Note that, the PZT extension increases linearly with the PZT temperature. In order to keep a constant strain or tension on the sample, we carefully adjusted the PZT voltage during the temperature-dependent experiment.
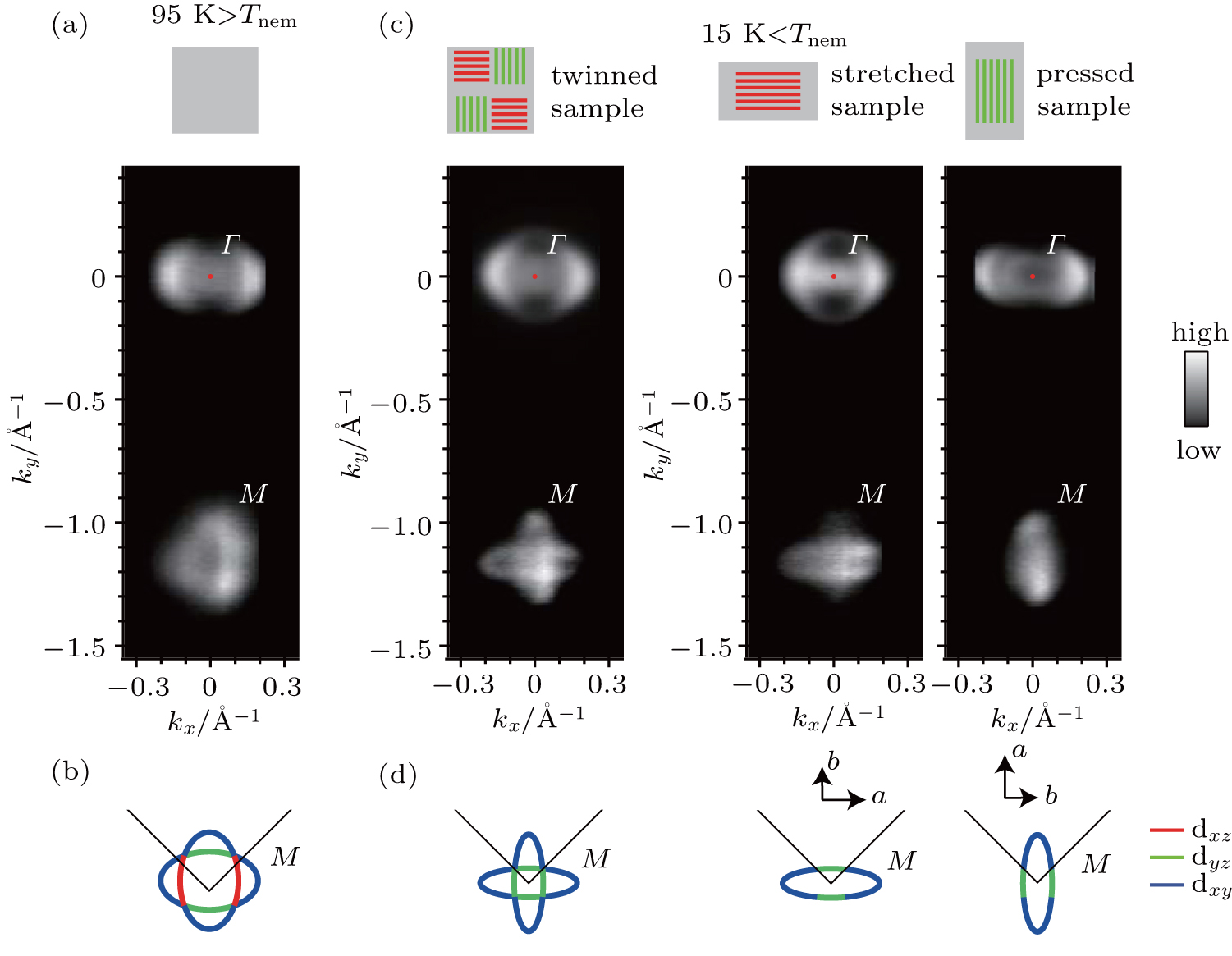
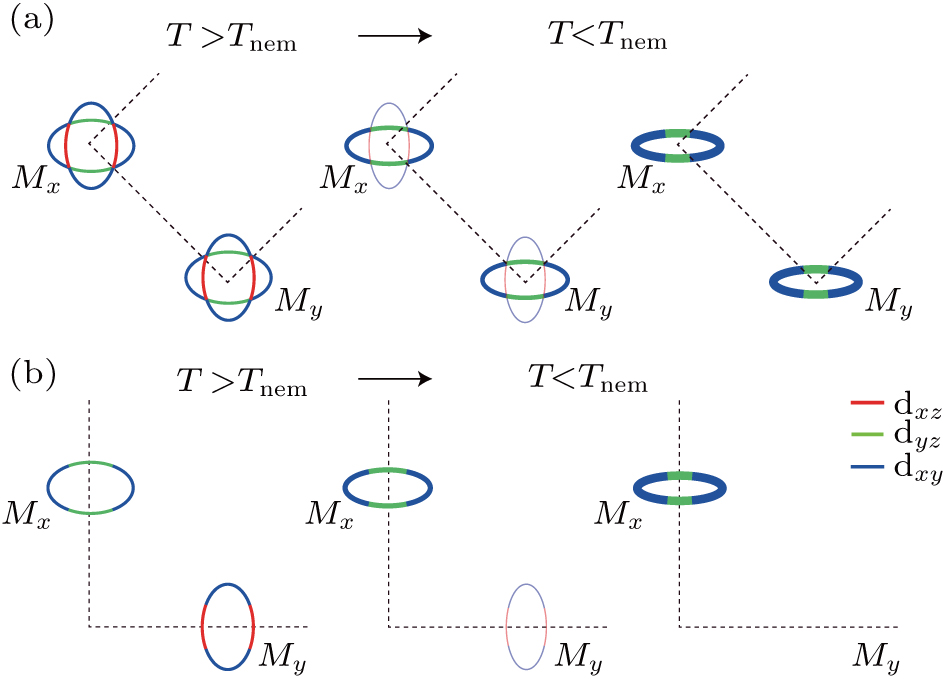
The Fermi surface of iron-based superconductors consists of hole pockets at the Brillouin zone center (Γ) and electron pockets at the Brillouin zone corner (M).[21] As shown in Figs.
Here, we define the longer axis of the lattice as the x axis. The orbital characters of the remaining electron pocket could be then attributed to the dyz and dxy orbitals.[12,13]
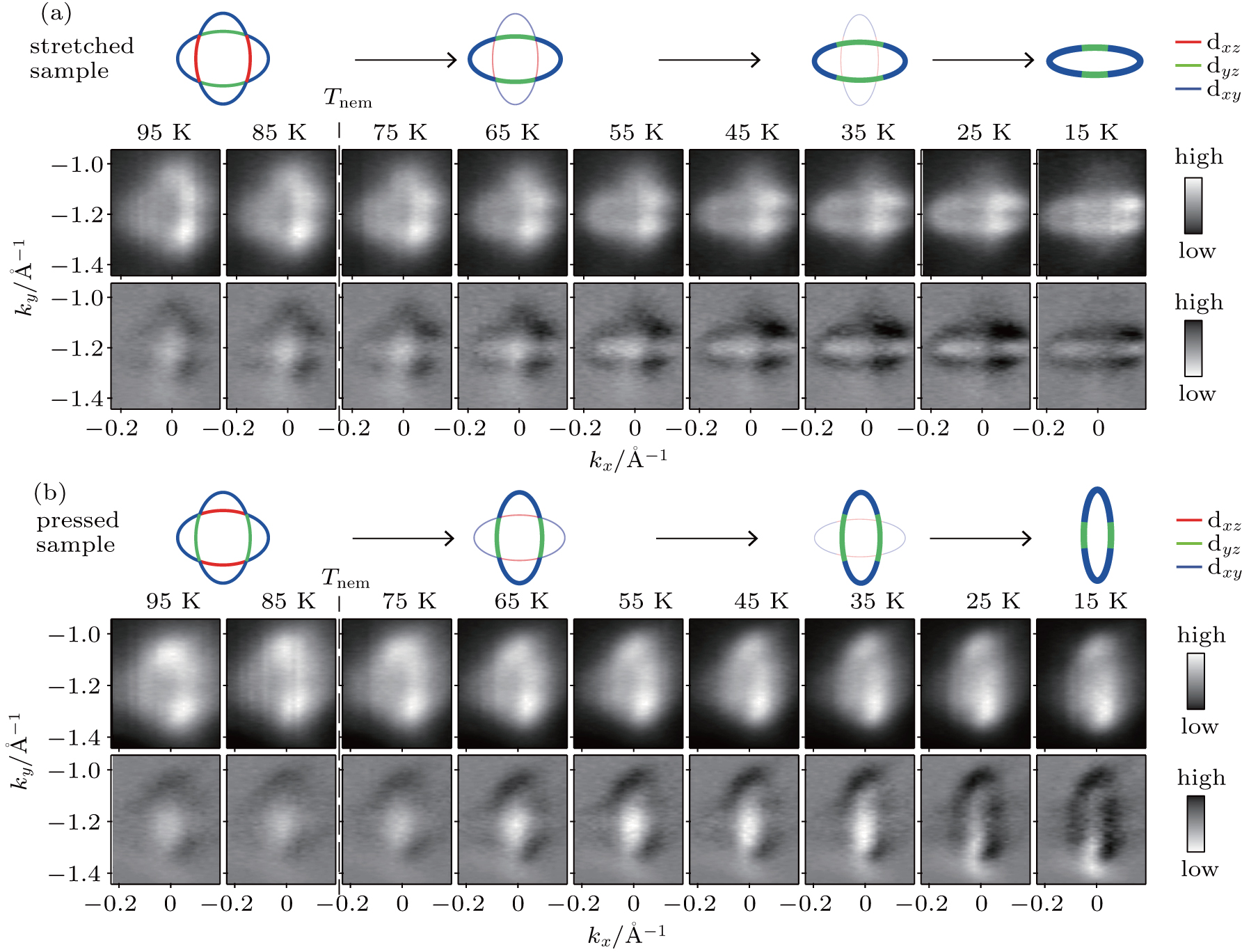
To understand how the Fermi surface evolves with temperature, we took the detailed temperature dependences of Fermi surface mapping in both the stretched and pressed samples. The data are shown in Fig.
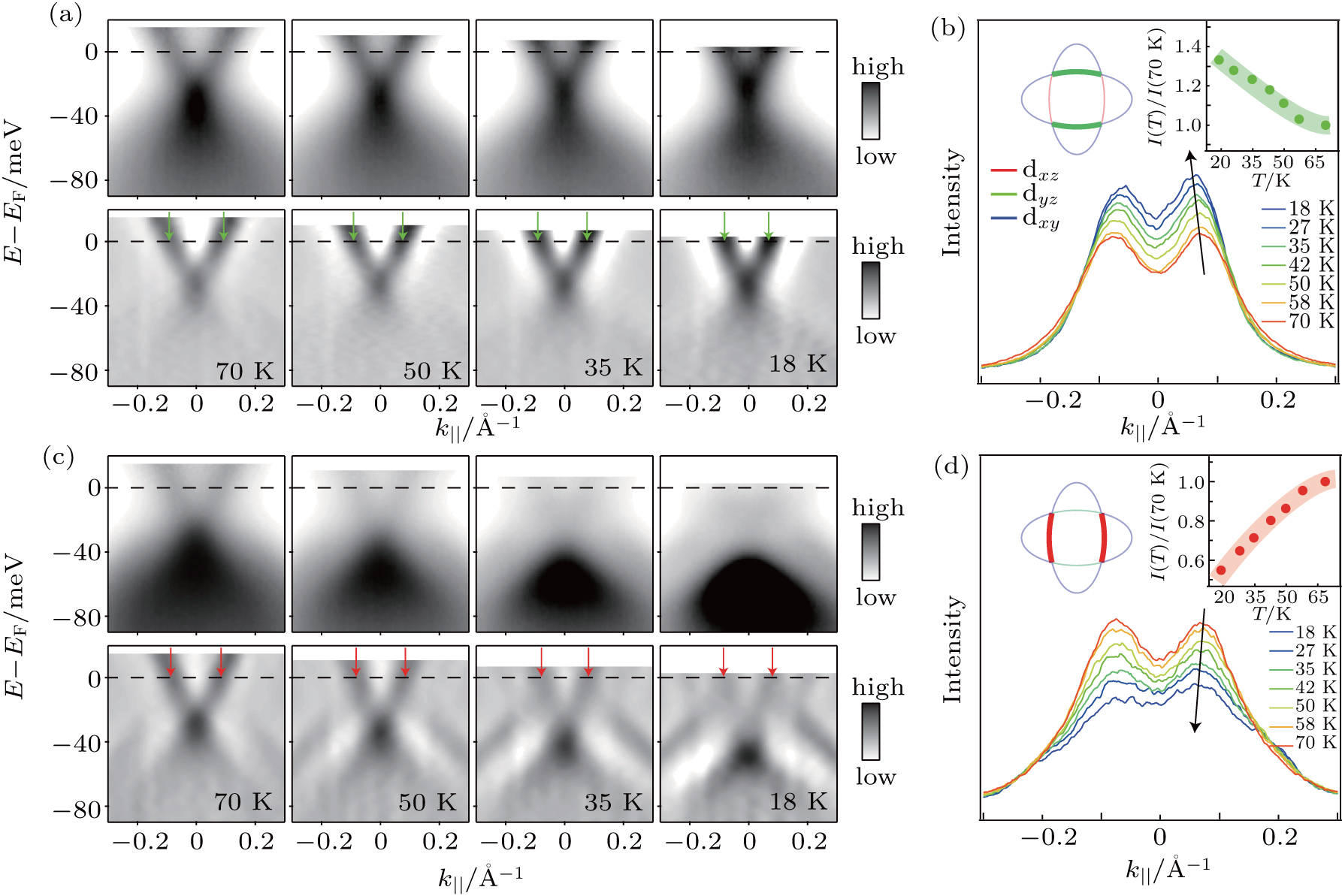
The electron pockets are constructed by the dxz, dyz, and dxz electron bands. By changing both the domain direction and the experimental orientation, we could probe different electron bands selectively.[23,24] Figure
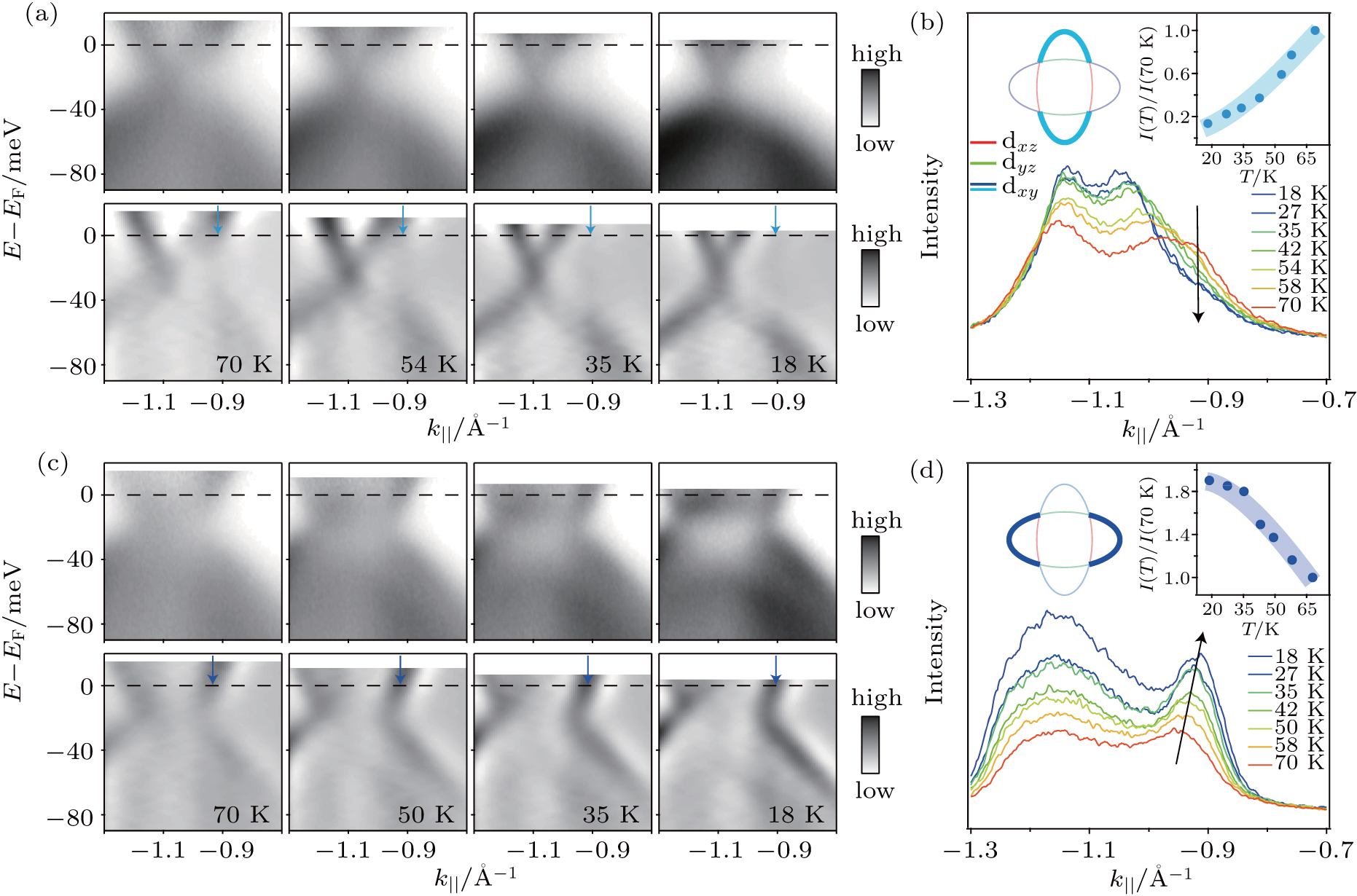
Similar temperature dependent behaviors were also observed on the dxy electron bands. The dxy electron bands disperse along both the vertical and horizontal directions. As shown in Fig.
Such spectral weight transfer has not been observed in previous ARPES experiments. One important reason is that the Tnems are high in most iron-based superconductors. As a result, the energy reconstruction of the bands is so pronounced which conceals the spectral weight modulation. For example, in a recent ARPES study on the detwinned FeSe,[13] the entire dxz electron band was found to be pushed above EF in the nematic phase. Therefore, it is difficult to observe the spectral weight loss of the dxz electron band. Moreover, in most iron-based superconductors, the reconstruction of Fermi surface is so strong that tracking the spectral weights of all the bands is very difficult. Here, in FeSe0.9S0.1, the energy scale of the band shift is reduced and the shape and size of the electron pockets change little with temperature. Therefore, quantitate analyses of spectral weight on all electron bands could be achieved.
Figure
Our results characterize the detailed temperature evolution of Fermi surface in the nematic phase. We show that not only the shape of electron pockets but also their spectral weights become anisotropic. Such reconstruction of Fermi surface could affect the pairing interaction of superconductivity. It is believed that the superconducting pairing is mediated by the inter-pocket scattering between the hole and electron pockets. The unbalanced orbital weight distributions or coherencies of the electron pockets would result in a pairing interaction that is strongly anisotropic and orbital-selective. This is consistent with previous ARPES and scanning tunnel microscopy studies showing that the superconducting gap is strongly anisotropy and orbital-dependent in FeSe.[29,30] Our results support the existence of orbital-selective pairing in FeSe, and provide crucial clues for understanding the pairing mechanism of the nematic superconducting phase.
In summary, we studied the reconstruction of electronic structure in the nematic phase of FeSe0.9S0.1. The detailed temperature evolutions of spectral weight were measured for all electron bands at the M point. We found that the rotational symmetry breaking is manifested by not only an anisotropic band dispersion but also a band-selective modulation of spectral weight. One electron pocket loses spectral weight and the Fermi surface consists of only one anisotropic electron pocket at the M point in the nematic phase. To fully understand the observed spectral weight transfer on the electron pockets, further experimental and theoretical studies are required. Our results complete our understanding of the symmetry-broken electronic state in the nematic phase, and also put strong constrains on constructing the theoretical models for both the nematic and superconducting phases in iron-based superconductors.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |