Cite this Article
Wang Peng, Zhang Ning-Chao, Jiang Cheng-Lu, Liu Fu-Sheng, Liu Zheng-Tang, Liu Qi-Jun. Structural, mechanical, and electronic properties of Zr – Te compounds from first-principles calculations. Chinese Physics B, 2020, 29(7): 076201  
Permissions
Structural, mechanical, and electronic properties of Zr – Te compounds from first-principles calculations
Wang Peng1, Zhang Ning-Chao1, †, Jiang Cheng-Lu2, Liu Fu-Sheng2, Liu Zheng-Tang3, Liu Qi-Jun2, ‡
School of Electronic and Information Engineering, Xi’an Technological University, Xi’an 710021, China
School of Physical Science and Technology, Key Laboratory of Advanced Technologies of Materials, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China
State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China

 

† Corresponding author. E-mail: ningchaozhang@163.com qijunliu@home.swjtu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11574254), the Key Research Project of Science and Technology Department of Shaanxi Province, China (Grant Nos. 2018GY-044 and 2017ZDXM-GY-114), the Innovation Talent Promotion Project of Shaanxi Province, China (Grant No. 2019KJXX-034), the Science and Technology Program of Sichuan Province, China (Grant No. 2018JY0161), and the Fund of the State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, China (Grant No. SKLSP201843).

Abstract

The first-principles calculations based on density functional theory are used to obtain structural, mechanical, and electronic properties of Zr–Te compounds. The optimized structural parameters are consistent with the available experimental data. The calculated mechanical properties and formation energy show that the Zr–Te compounds are all mechanically and thermodynamically stable. The bulk modulus B, shear modulus G, Young’s modulus E, Debye temperature ΘD, and sound velocity vm are listed, which are positively correlated with the increasing of atomic fraction of Zr. The behaviors of density of states of Zr–Te compounds are obtained. Furthermore, the electronic properties are discussed to clarify the bonding characteristics of compounds. The electronic characteristics demonstrate that the Zr–Te systems with different phases are both covalent and metallic.

PACS: ;62.20.-x;;63.20.dk;;64.70.kd;
Keyword:;Zr-Te compounds;;first-principles calculations;;mechanical properties;
1. Introduction

Zr-based bulk amorphous alloys play a significant role in the history of alloys,[1] and have aroused the wide interest in glass-forming ability to become bulk metallic glasses.[2–5] The first synthesized metallic glasses were reported in 1960,[6] which contained zirconium. Zirconium is non-toxic and Zr-based alloys show good biocompatible ability, so that they can be used as biomedical materials.[7] Besides, Zr-based alloys possess wide applications in battery cathodes,[8] solar cells,[9] nuclear industry,[10] and transistors.[11] Recently, many researchers have investigated Zr–Te compounds in order to develop their advanced applications in superconductors, thermoelectric materials, spintronics/quantum computing, flexible electronics,[11–16] thus showing their huge potential applications in the electronic industry. Superconductivity of ZrTe3 was found under pressure by measuring the resistivity of single crystal, and no structural phase transition was observed.[12] The ZrTe5 was predicted to be a good thermoelectric material due to its large Seebeck coefficient and good electric conductivity.[13] Temperature-dependent resistivity and magneto-transport characterizations of polycrystalline ZrTe5 – δ have been reported,[14] indicating that it is a p-type semiconductor. In addition, the structural, elastic, electronic, and transport properties of semimetal ZrTe have been investigated.[15,16] It can be seen that different compositions of Zr and Te result in different physical properties and various applications. However, it is quite lacking in thorough and systematic investigations of Zr–Te compounds.

In order to offer a comparative study between Zr–Te compounds, the fundamental properties of ZrTe, ZrTe3, ZrTe5, Zr2Te, Zr3Te, Zr5Te4, and Zr5Te6[17–25] are investigated by using the first-principles calculations, which include structural, elastic, mechanical, and electronic properties.

2. Computational methods

All calculations were performed with CASTEP code[26] based on the density functional theory (DFT). The local density approximation (LDA) with the Ceperley–Alder–Perdew–Zunger (CA-PZ) functional[27] was employed as the exchange-correlation functional due to the fact that the LDA can better describe the electronic characteristics of metals. Using plane-wave expansions, the wave functions of Kohn–Sham[28] were expanded. The Monkhorst–Pack k-points were used to optimize the structures for the sampling of Brillouin zone, including 3 × 7 × 4, 8 × 8 × 8, 4 × 6 × 3, 7 × 7 × 2, 1 × 7 × 2, 2 × 2 × 4, 2 × 2 × 7, and 2 × 2 × 4 for orthorhombic ZrTe, hexagonal ZrTe, monoclinic ZrTe3, orthorhombic ZrTe5, orthorhombic Zr2Te, tetragonal Zr3Te, tetragonal Zr5Te4, and trigonal Zr5Te6, respectively. A total energy convergence of 5.0× 10−6 eV/atom was set during the structural optimization.

3. Results and discussion
3.1. Structural optimization

The crystal structures of Zr–Te compounds are shown in Fig. 1. The ZrTe crystallizes into orthorhombic (Pnma) and hexagonal (P-6m2) structures. ZrTe3, ZrTe5, Zr2Te, Zr3Te, Zr5Te4, and Zr5Te6 belong to monoclinic, orthorhombic, orthorhombic, tetragonal, tetragonal, and trigonal structures, respectively. Their correspongding space groups are P21/m, Cmcm, Pnma, I-4, I4/m, and P-3m1, respectively. The optimized lattice parameters of Zr–Te compounds along with pure bulk Te and Zr are listed in Table 1. The corresponding experimental values[17–25,29,30] are also shown. It can be seen that the calculated data are consistent with previous results. The relationship between density and Zr content is shown in Fig. 2. It can be seen that the density increases with Zr content increasing until ZrTe phase appears, then it fluctuates with Te content decreasing. Due to the density of pure Zr being similar to that of Te, the relatively large density means closer arrangement and may exhibit better mechanical properties. Hence, according to the calculated density, we deduce that ZrTe (P-6m2) phase has better mechanical properties and ZtTe5 phase has poorer mechanical properties.

Fig. 1. Crystal structures (Zr in blue, Te in orange) of (a) orthorhombic ZrTe, (b) hexagonal ZrTe, (c) monoclinic ZrTe3, (d) orthorhombic ZrTe5, (e) orthorhombic Zr2Te, (f) tetragonal Zr3Te, (g) tetragonal Zr5Te4, and (h) trigonal Zr5Te6.
Fig. 2. Plots of density versus Zr content.
Table 1.

Calculated lattice parameters of Zr–Te compounds along with experimental data.[17–25,29,30]

.
3.2. Formation energy

In order to evaluate thermodynamic stability, the formation energy values are calculated for these considered cases. The negative formation energy indicates that the reaction is an exothermic reaction and the final compound is thermodynamic stability. The computed equation of formation energy (Δ H) is given as follows:

where , , and refer to the total energy value of ZrxTey compounds, Zr and Te in the solid states, respectively. Table 2 shows the calculated formation energy values of Zr–Te compounds. From our calculations, the Zr–Te compounds are found to be thermodynamically stable due to their formation energy values are all negative.

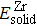
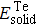
Table 2.

Calculated formation energy values of Zr–Te compounds.

.

As shown in Fig. 3, the relationship between formation energy and Zr content indicates that the formation energy first decreases to a minimum value of –1.017 eV/atom of hexagonal ZrTe at 50% Zr content, then rises with Zr content increasing.

Fig. 3. Plot of formation energy versus Zr content.
3.3. Mechanical stability and properties

The elastic constants of Zr–Te compounds are calculated to estimate their mechanical stability by the stress–strain calculations in their optimized crystal structures. The lattice energy for expanding elastic strain and the elastic constants are given as follows:[31]

where E, E0, V0, ε, and i/j represent the total energy with tiny deformation, total energy at equilibrium state, equilibrium volume, elastic strain, and tensor index, respectively. The calculated independent elastic constants of Zr–Te compounds are shown in Table 3. It is well known that the crystal is considered to be mechanically stable when the quadratic form from elastic constants’ matrix is always positive.[32] Hence, the Born stability criteria for hexagonal, tetragonal, trigonal, orthorhombic, and monoclinic structures are shown as follows:

for hexagonal phase,

for tetragonal phase,

for trigonal phase,

for orthorhombic phase,

monoclinic phase

In Table 3, the calculated elastic constants Cij of Zr–Te compounds show that all structures are mechanically stable. The elastic constants show the deformation-resistance of materials in different lattice directions, which are defined by stress/strain. From our calculated results, it can be seen that the biggest deformation-resistant value of 214.67 GPa appears in P-6m2 ZrTe, showing high hardness along z axis. The ZrTe5 has a weak deformation-resistant due to lower elastic constants, so it is the softest material in Zr–Te compounds.

Table 3.

Calculated elastic constants of Zr–Te compounds.

.

As is well known, the elastic constants are associated with the single crystal and the elastic modulus is linked with the polycrystal.[33–35] Then, we introduce three methods to calculate elastic modulus, i.e., the Voigt, Reuss, and Hill methods,[33–36] which are related to the upper, lower, and average bounds of elastic constants, respectively.

Tetragonal, orthorhombic, and monoclinic phases are

Trigonal and hexagonal phases are

Sij represents elastic compliances which can be obtained by elastic constants.

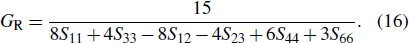
Then, bulk modulus B and shear modulus G are calculated by the Voigt–Reuss–Hill (VRH) method[33]

The Young’s modulus (E), Poisson’s ratio (v), average sound velocity (vm), longitudinal sound velocity (vl), transverse sound velocity (vt), Debye temperature (ΘD), and Vickers hardness (Hv) are obtained as follows:[34–37]

where h, kb, NA, M, ρ, n, and Va are Planck’s constant, Boltzmann’s constant, Avogadro’s number, molecular weight, density, number of atoms per unit cell, and unit volume, respectively.

Table 4 shows basic mechanical parameters of compounds, covering the bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio v, Debye temperature ΘD, sound velocity vm, and Vickers hardness Hv. The bulk modulus can be positive in a certain condition (changing pressure/volume). The bulk modulus shows the ability of materials to maintain crystal structure and to resist deformation under hydrostatic pressure. The calculated results of bulk modulus are in the following order: ZrTe5 (25.38 GPa) < ZrTe3 (41.99 GPa) < Zr5Te4 (65.04 GPa) < Zr5Te6 (68.03 GPa) < orthorhombic ZrTe (102.42 GPa) < hexagonal ZrTe (110.23 GPa) < Zr3Te (116.19 GPa) < Zr2Te (119.93 GPa). The ZrTe5 with bulk modulus 25.38 GPa is predicted to be the softest compound, and the hardest one is Zr2Te (119.93 GPa). The shear modulus can be obtained by shear stress/shear strain. The shear modulus is a critical parameter to quantify the deformability of axis, that is, the big shear modulus of materials presents a good resistance to shaping the change. The shear modulus values in Zr–Te systems follow an order of ZrTe5 (15.16 GPa) < ZrTe3 (21.52 GPa) < Zr5Te4 (39.43 GPa) < Zr3Te (43.81 GPa) < Zr5Te6 (45.41 GPa) < orthorhombic ZrTe (51.75 GPa) < Zr2Te (61.60 GPa) < hexagonal ZrTe (66.59 GPa). The Young’s modulus is defined by normal stress/normal strain, which is a popular way to show the normal mechanical properties. The biggest value can be found in ZrTe (P-6m2) to be 166.29 GPa. So ZrTe (P-6m2) is a good compound to resist normal deformation, comparing with the ZtTe5 with a least Young’s modulus of 37.93 GPa. The velocity vm is obtained through changing the pressure and volume, which shows the speed of changing of resisting deformation of materials. The velocity is in a range from 1713.71 (m/s) to 3216.04 (m/s) for all compounds. Debye temperature displays the thermal conductivity of crystalline solid.[38] In Table 4, it can be seen that the high Debye temperature is associated with high modulus. Moreover, Debye temperature describes the vibrational information and thermodynamic information. Debye temperatures for all compounds range from 151.65 K to 337.09 K. Vickers hardness can be used to investigate the wear resistance of material, and the calculated Vickers hardness values for Zr–Te compounds are in a range from 3.51 GPa to 10.14 GPa. It can be noticed that ZrTe with P-6m2 space group is the hardest, and ZrTe5 is the softest in these compounds. Moreover, in order to judge the ductility or brittleness of a material, the G/B ratio is introduced.[39] The critical value for distinguishing ductile and brittle materials is 0.57 and a low G/B value is linked with the ductility. According to the calculated results in Table 4, ZrTe with Pnma space group, ZrTe3, Zr2Te and Zr3Te show ductile behaviors, and the others exhibit brittle behaviors.

Table 4.

Calculated values of bulk modulus B (in unit GPa), shear modulus G (in unit GPa), Young’s modulus E (in unit GPa), Poisson’s ratio v, sound velocity vm (in units m/s), Debye temperature ΘD (K), Vickers hardness Hv (GPa) and G/B ratio of Zr–Te compounds.

.

In Fig. 4, the bulk modulus B, shear modulus G, Young’s modulus E, Debye temperature ΘD, and sound velocity vm change dependently with the increase of atomic fraction Zr. It is necessary to discuss Pearson correlations[40] as shown in Table 5. The correlation coefficient represents the positive relationship among variable quantities, and the significant level indicates the reliability of correlation coefficient.[40,41] The great value (R = 0.998) indicates that the strongest positive relationship occurs between Young’s modulus and shear modulus. The minimum value (R = 0.895) with sig = 0.001 indicates that it shows a positive relationship between sound velocity and bulk modulus. According to Pearson correlations, it can be seen that the bulk modulus B, shear modulus G, Young’s modulus E, and Debye temperature ΘD are dependent on the quantity of Zr element.

Fig. 4. Plots of bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), Debye temperature ΘD (K), and sound velocity vm (m/s) of Zr–Te compounds versus atomic fraction Zr.
Table 5.

Pearson correlation (Corr) and significant level (sig) of calculated bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), Debye temperature ΘD (K), and sound velocity vm (m/s) for Zr–Te compounds.

.
3.4. Electronic properties

In order to show the electronic properties of Zr–Te compounds, the total densities of states (TDOSs) of Zr–Te compounds are shown in Fig. 5. The Fermi level is set to be 0 eV. At the Fermi level, the non-zero values occur in TDOS, indicating that Zr–Te compounds show metallic characters. Further research shows that the ZrTe5 is semimetallic due to its very small band gap of 0.002 eV. In order to accurately obtain the band gap of ZrTe5, the HSE06 functional is used here. The calculated band gap is 0.006 eV, which is shown in Fig. 6. Although Chen et al. found that polycrystalline ZrTe5– δ was a p-type semiconductor, whether the ZrTe5 is a semiconductor or a semimetal is still an open question.[14] Metallic character of compound with covalent bonds relates to the pseudogap in the DOS. The pseudogap is set by the two peaks on either hand (one below and the other above) near Fermi level (Ef). The pseudogap occurs at Fermi level of compound, which shows that the electron clouds are shared and the covalent behaviors appear. The stronger covalent bond is associated with the deeper splitting shape of pseudogap.[34–36] In Fig. 5, the remarkable pseudogaps are observed in ZrTe, ZrTe3, and ZrTe5, indicating these cases behaves in a covalent manner. By contrast, Zr2Te, Zr3Te, Zr5Te4, and Zr5Te6 have obvious metallic characteristics. In addition, the DOSs of Zr–Te compounds are divided into four parts, which are identical as shown Fig. 5. It can be noticed that the more similar the shapes of curves, the more alike their bulk moduli are.

Fig. 5. Plots of TDOS versus energy of ZrTe compounds.
Fig. 6. Band structure of ZrTe5.

The charge densities of Zr–Te compounds are calculated to further analyze the electronic states. In Fig. 7, the charge densities between Zr and Te are illustrated. It can be seen that all the Zr–Te compounds have covalent characteristics due to the sharing of electron clouds. The formed “head to head” σ bond between atom Zr and atom Te can be observed in all compounds, which can also be found between Te and Te in ZrTe5 ().

Fig. 7. Calculated charge densities of Zr–Te compounds: (a) ZrTe (Pnma) (010), (b) ZrTe (P-6m2) (111), (c) ZrTe3 (010), (d) ZrTe5 (), (e) Zr3Te (010), (f) Zr2Te (010), (g) Zr5Te6 (111), and (h) Zr5Te4 (111).
4. Conclusions

The first-principles calculations are carried out to investigate the geometrical structures, phase stability, mechanical properties and electronic structures of Zr–Te compounds. The negative formation energy values reveal that these compounds are thermodynamically stable. These compounds are also mechanically stable according to the mechanical stability criteria. The mechanical properties of Zr–Te compounds are calculated and discussed. The ZrTe5 has the lowest bulk modulus of 25.38 GPa, and Zr2Te has the largest bulk modulus of 119.93 GPa. For shear modulus and Young’s modulus, the biggest values both appear in ZrTe (P-6m2) phase, and the least values both appear in ZtTe5 phase. Correspondingly, the ZrTe (P-6m2) phase shows a maximum sound velocity, Debye temperature, and Vickers hardness, and the ZtTe5 phase presents the smallest value, which is due to the bonding force between atoms. The ZrTe possesses Pnma space group, and ZrTe3, Zr2Te, and Zr3Te belong to ductile compounds according to the analysis of G/B, and the others belong to brittle compounds. Moreover, the bulk modulus B, shear modulus G, Young’s modulus E, Debye temperature ΘD, and sound velocity vm are positive correlation with the increase of fraction Zr. The calculated electronic properties show that Zr–Te compounds have metallic characters except ZrTe5. Whether ZrTe5 is a metal or a semimetal needs further studying. The charge densities of Zr–Te compounds indicate the forming of σ bond between atom Zr and atom Te.

Reference
[1] Inoue A 1996 Sci. Rep. RITU A 42 1
[2] Gao X Q Sun Y T Wang Z Li M Z Bai H Y 2017 Chin. Phys. 26 016101
[3] Conner R D Li Y Nix W D Johnson W L 2004 Acta Mater. 52 2429
[4] Jiang S Q Huang Y Li M Z 2019 Chin. Phys. 28 046103
[5] Inoue A Zhang W Zhang T Kurosaka K 2001 Acta Mater. 49 2645
[6] Jun W K Willens R H Duwez P O L 1960 Nature 187 869
[7] Lin M T Wan C H Wu W 2017 Surf. Coat. Technol. 320 217
[8] Abdulsalam M Joubert D P 2016 Phys. Status Solidi 253 868
[9] Abdulsalam M Joubert D P 2015 Eur. Phys. J. 88 177
[10] Zander D Köster U 2004 Mater. Sci. Eng. 375--377 53
[11] Morozova N V Korobeinikov I V Kurochka K V Titov A N Ovsyannikov S V 2018 J. Phys. Chem. 122 14362
[12] Gu K Susilo R A Ke F Deng W Wang Y J Zhang L K Xiao H Chen B 2018 J. Phys.: Condens. Matter 30 385701
[13] Wang C Wang H F Chen Y B Yao S H Zhou J 2018 J. Appl. Phys. 123 175104
[14] Chen S S Li X Lv Y Y Cao L Lin D J Yao S H Zhou J Chen Y B 2018 J. Alloys Compd. 764 540
[15] Ullah S Wang L Li J X Li R H Chen X Q 2019 Chin. Phys. 28 077105
[16] Guo S D Wang Y H Lu W L 2017 New J. Phys. 19 113044
[17] Örlygsson G Harbrecht B 2001 J. Am. Chem. Soc. 123 4168
[18] Örlygsson G Harbrecht B 1999 Z. Naturforsch. 54 1125
[19] Furuseth S Fjellvag H 1991 Acta Chem. Scand. 45 694
[20] Furuseth S Brattas L Kjekshus A 1975 Acta Chem. Scand. 29 623
[21] Fjellvag H Kjekshus A 1986 Solid State Commun. 60 91
[22] Öerlygsson G Harbrecht B 1999 Inorg. Chem. 38 3377
[23] Harbrecht B Leersch R 1996 J. Alloys Compd. 238 13
[24] de Boer R Cordfunke E H P van Vlaanderen P Ijdo D J W Plaisier J R 1998 J. Solid State Chem. 139 213
[25] Öerlygsson G Harbrecht B 2000 Chem. - A Eur. J. 6 4170
[26] Segall M D Lindan P J D Probert M J Pickard C J Hasnip P J Clark S J Payne M C 2002 J. Phys.: Condens. Mater 14 2717
[27] Ceperley D M Alder B 1980 Phys. Rev. Lett. 45 566
[28] Kohn W Sham L J 1965 Phys. Rev. 140 A1133
[29] Campos C E M Ersching K de Lima J C Grandi T A Höhn H Pizani P S 2008 J. Alloys Compd. 466 80
[30] Olinger B Jamieson J C 1973 High Temperatures-High Press. 5 123
[31] Born M Huang K 1954 Dynamical Theory of Crystal Lattices Oxford Oxford University Press
[32] Mouhat F Coudert F 2014 Phys. Rev. 90 224104
[33] Hill R 1952 Proc. Phys. Soc. Lond. 65 349
[34] Li P Ma L S Peng M J Shu B P Duan Y H 2018 J. Alloys Compd. 747 905
[35] Bao W Z Liu D Duan Y H 2018 Ceram. Int. 44 14053
[36] Wu Z J Zhao E J Xiang H P Hao X F Liu X J Meng J 2007 Phys. Rev. 76 054115
[37] Tian Y Xu B Zhao Z 2012 Int. J. Refract. Met. Hard Mater 33 93
[38] Kanchana V Vaitheeswaran G Svane A Delin A 2006 J. Phys: Condens. Matter 18 9615
[39] Pugh S F 1954 Philos. Mag. 45 823
[40] Rodgers J L Nicewander W A 1988 Am. Statistician 42 59
[41] Rice W R 1989 Evolution 43 223