† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11504135) and University Science and Technology Plan Project of Shandong Province, China (Grant Nos. J16LJ53).
We theoretically study the reversible process of quantum entanglement state by means of weak measurement and corresponding reversible operation. We present a protocol of the reversion operation in two bodies based on the theory of reversion of single photon and then expend it in quantum communication channels. The theoretical results demonstrate that the protocol does not break the information transmission after a weak measurement and a reversible measurement with the subsequent process in the transmission path. It can reverse the perturbed entanglement intensity evolution to its original state. Under the condition of different weak measurement intensity the protocol can reverse the perturbed quantum entanglement system perfectly. In the process we can get the classical information described by information gain from the quantum system through weak measurement operation. On the other hand, in order to realize complete reversibility, the classical information of the quantum entanglement system must obey a limited range we present in this paper in the reverse process.
The no-cloning theorem prohibits the arbitrary copying of quantum states because of the linearity of quantum mechanics.[1] This seems difficult to obtain some information from quantum communication (QC) process in another way.[2–12] In quantum information fields it is of challenge how to get some information from QC without destroying its transmission process. However, weak measurement[13–19] and reversing operation may make it possible to solve the above problem. A scheme of reversion of a weak-measurement quantum system for a photonic qubit and finite photo number was established,[15,20] and then a tight bound was present between information gain and reversibility in weak measurement and it testifis that the information extracted from a weak measurement is erased by the reversing process.[21] If the techniques can be applied in QC process, we may obtain some information from QC and it does not destroy the normal communication process. Although quantum entanglement state guarantees high confidentiality by the quantum no-cloning theorem in the process of QC, if we do not copy or destroy the quantum entanglement state, whether we can get some information from the QC process will be the focus problem of our concern. We hope that the techniques investigated in this paper can be used in the QC process. A quantum system can not be recovered to its initial state after projection measurement. It makes the initial state collapse to one of the eigenstates irrevocably. If a weak measurement acts on a quantum system, it can be reversed to the original state by a successful reversing operation and the information extracted from a weak measurement can be erased by reversibility operation. How much weak measurement intensity can be sustained for quantum system without affect QC process and whether it can achieve completely reversible operation of quantum entanglement states are the problems of our concern in this paper.
In QC and quantum information, entanglement state plays a crucial role. However, environment effects on a entanglement system make its entanglement intensity decline rapidly.[22–26] Although there are several ways to increase its intensity,[27–30] we can well perform QC process if the initial entanglement state has strong capacity of resisting disturbance. Thus, selecting high quality entanglement state is also a significative work. Therefore, several important problems need to be discussed: whether weak measurement and reversing operation can be applied in QC process perfectly, whether there is a bound to restrict the weak measurement intensity and how to select a high quality entanglement state.
In this paper, we study the reversion of a perturbed entanglement system and provide a protocol by use of the scheme of QC and the double Jaynes–Cummings (D-J-C) model.[31–33] We demonstrate the feasibility of the reversing weak-measurement quantum system in QC process, and derive the condition of complete reversibility of multi-part entanglement channels. There is contradiction between weak measurement intensity and complete reversibility: the more the entangled particles we have, the less the classical information will be obtained. We give a scheme of identifying dual or triple quantum entanglement states and it can be extend to a multiple entanglement system.
This paper is organized as follows. In Section
As it is known that QC transfers an unknown quantum state from one location to a distant one based on the quantum no-cloning theorem by use of non-local correlation of entanglement and classical means,[8–10] as an example of QC, can teleport quantum state from here to there without any trajectory in space using pre-established entanglement as a channel.[2–4,11,12] The scheme of quantum teleportation is shown in Fig.
Based on the above scheme, our constructions of reversion of quantum entanglement state also rely on the theory of reversion of single photonic qubit.[20,21] We will thus first briefly review certain definitions and properties related to reversion of a photonic qubit, such as weak measurement, reversion operation, information gain, reversibility. Quantum measurement is an indispensable part of QC and weak measurement is another focus of attention.[14] The main point of weak measurement is valid and its essential part is a detector. It has also been regarded as a role in reformulating quantum theory.[34] The projection operator measurements make quantum state collapse to one of the eigenstates and the initial state can never be recovered after the projection measurement. If a weak measurement is made in path 1 or path 2 and a reversing operation is made subsequently, then we can reverse the weak-measurement quantum system. It is feasible to obtain the information from QC process that does not impact the subsequent QC by reverse operation, and it is possible to reverse the partial measurement-induced state collapse that can be served as a probabilistic quantum error correction.[20,35] Weak measurement, different from orthogonal projection measurement, is not sharp and its outcome is not precise but nevertheless reveals some information about the system. The information of the initial state can pass over to the final state because the weak measurement does not totally collapse the system.[15,16] The reversibility of a photonic qubit is discussed in Ref. [20]. A detector of weak measurement clicks with a probability η if the qubit is in the state |1〉 and never clicks if the qubit is in the state |0〉. From the result of the detector we can get some partial information about the initial state, which can be used to guess the initial state. If make a normal projection measurement on the detector by the measurement operator 

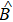


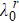
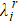
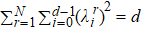
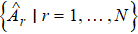
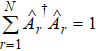


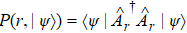

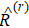
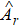
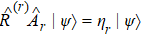


Combined the above model and theories, we investigate revering weak-measurement quantum entanglement state in quantum communication. We employ the reversible operation and quantum communication scheme to investigate the reversibility of quantum entanglement intensity in the process of information transfer. If we make a weak measurement on the transmission path 1 or path 2 and then make a reversible measurement on the subsequent process, we can get some information about the system and do not impact the information transmission. In order to explore whether it can reverse perturbed two-body entanglement intensity to its initial state, we make use of the double Jaynes’Cummings model[31] to analyze feasibility of revering process. It is convenient to analyze the reversion of two particle entanglement state and to apply the protocol into quantum communication by using this model. In the propagation path 1 or path 2, we embed two vacuum cavities in proper order, conveniently for the task of weak measurement and reversible measurement, as shown in Fig.
Firstly, let us assume that atoms A and B are entangled and identical from the entanglement resource, taking one of Bell’s type entanglement states as initial state



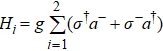
Then suppose that a weak measurement is operated by 
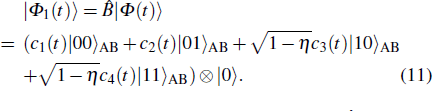
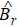

Finally, we calculate the entanglement intensity of the initial state and the state after reversible operation by the entanglement negativity[37–39] of the quantum system, which can be expressed as

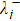
Combined with the above formulas, the negativity of entanglement state after weak measurement and reversible operation can be obtained. Here we consider the maximum entanglement state 
The formulas of negativity of initial quantum system is as follows:

The formulas of negativity of the weak-measurement quantum system is

The formulas of reversed negativity of the weak-measurement quantum system is

Figure
However, the system is limited by the relation of information gain and reversibility, in order to achieve complete reversibility, it must satisfy Gmax ≤ 1/4 of two-body entanglement state and the multi-body entanglement state should satisfy Gmax ≤ 1/2n for the n-particle entanglement system. In order to ensure the complete reversibility of the entanglement system, the weak measurement intensity must be limited within a certain range. On the other hand, based on the balance between information gain and reversibility, in order to get the information, the two-body quantum entanglement system should obey the relation 20Gmax + 3Prev ≤ 8. Under the condition Prev = 0, the information gain is Gmax = 2/5. When Prev = 1, Gmax = 1/4. In the range of 1/4 < Gmax < 2/5, we can achieve partial reversibility of the entangled system. In order to achieve complete reversibility, it must satisfy Gmax ≤ 1/4. In a similar way, the information gain must satisfy Gmax ≤ 1/8 for the three-body entanglement system and it should satisfy Gmax ≤ 1/2n for the n-particle entanglement system. That is to say, under the condition of complete reversibility, we will get less information as the number of particle entanglement increases.
From the above discussion, we can draw a conclusion that for an n-particle entanglement system after weak measurement the condition to realize complete reversibility is



We transfer the reversibility scheme of a single photon to the reversibility analysis of an entanglement system. Based on the theory of the D-J-C model and weak measurement operation, the reversibility of two-body entanglement is studied by taking Bell’s type entanglement state as an example. The result indicates that entanglement intensity of the weak-measurement quantum entanglement system can be reversed to its initial state. However it is limited by the relation of information gain and reversibility. In order to achieve complete reversibility, it must satisfy Gmax ≤ 1/4 of the two-body entanglement state and the multi-body entanglement state should satisfy Gmax ≤ 1/2n for n-particle entanglement system. Thus in order to ensure the complete reversibility of the entanglement system, the weak measurement intensity must be limited within a certain range. In addition, under the protocol of the above discussion, we can get some classical information about the quantum system by weak measurement. Here we only investigate the reversion of a weak-measurement entanglement system by one of the D-J-C model paths. We will continue to make further study considering both paths. It is wonder whether it is useful to apply in QC, and further analysis is needed for the connection between information gain and quantum entanglement systems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |







