† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11765016 and 11675113), the Natural Science Foundation of Beijing, China (Grant No. KZ201810028042), and Beijing Natural Science Foundation, China (Grant No. Z190005).
Quantum entanglement plays essential roles in quantum information processing. The monogamy and polygamy relations characterize the entanglement distributions in the multipartite systems. We present a class of monogamy inequalities related to the μ-th power of the entanglement measure based on Rényi-α entropy, as well as polygamy relations in terms of the μ-th power of Rényi-α entanglement of assistance. These monogamy and polygamy relations are shown to be tighter than the existing ones.
Quantum entanglement is one of the most quintessential features of quantum mechanics, which distinguishes the quantum world from the classical one and plays essential roles in quantum information processing,[1–5] revealing the basic understanding of the nature of quantum correlations. One distinct property of quantum entanglement is that a quantum system entangled with another system limits its sharing with other systems, known as the monogamy of entanglement.[6,7] The monogamy of entanglement can be used as a resource to distribute a secret key which is secure against unauthorized parties.[8,9] It also plays a significant role in many fields of physics such as foundations of quantum mechanics,[34,10] condensed matter physics,[11] statistical mechanics,[34] and even black-hole physics.[12,13]
The monogamy inequality was first introduced by Coffman–Kundu–Wootters (CKW) by using tangle as a bipartite entanglement measure in three-qubit systems,[14] and then generalized to multiqubit systems based on various entanglement measures.[15] The assisted entanglement is a dual concept to bipartite entanglement measure, which shows polygamy relations in multiparty quantum systems. For a three-qubit state ρABC, a polygamy inequality was introduced as[16] τa(ρA|BC)≤τa (ρA|B) + ρa(ρA|C), where τa(ρA|BC) = max ∑ipi τ(|ψi 〉A|B) is the tangle of assistance,[17,16] with the maximum taking over all possible pure state decompositions of ρAB = ∑i pi | ψi 〉AB 〈 ψi|. This tangle-based polygamy inequality was extended to multiqubit systems and also high-dimensional quantum systems in terms of various entropy entanglement measures.[18,19] General polygamy inequalities of entanglement are also established in arbitrary dimensional multipartite quantum systems.[20–25]
In this paper, we investigate the monogamy and polygamy constraints based on the μ-th power of entanglement measures in terms of the Rényi-α entropy for multiqubit systems. By using the Hamming weight of binary vectors, we present a class of monogamy inequalities for multiqubit entanglement based on the μ-th power of Rényi-α entanglement (RαE)[26] for μ ≥ 1. For 0 ≤ μ ≤ 1, we introduce a class of tight polygamy inequalities based on the μ-th power of the Rényi-α entanglement of assistance (RαEoA). Then, we show that both the monogamy inequalities with μ ≥1 and the polygamy inequalities with 0≤ α ≤ 1 can be further improved to be tighter under certain conditions. These monogamy and polygamy relations are shown to be tighter than the existing ones. Moreover, our monogamy inequality is shown to be more effective for the counterexamples of the CKW monogamy inequality in higher-dimensional systems.
We first recall the conceptions of Rényi-α entropy, Rényi-α entanglement, and multiqubit monogamy and polygamy inequalities. For any α > 0, α ≠ 1, the Rényi-α entropy of a quantum state ρ is defined as[27]

The Rényi-α entanglement (RαE) Eα (|ψ 〉AB ) of a bipartite pure state |ψ 〉AB is defined as


As a dual concept to RαE, the Rényi-α entanglement of assistance (RαEoA) is introduced as

For any multiqubit state ρAB0 ⋯ BN – 1, a monogamous inequality has been presented in Ref. [28] for α ≥ 2,

In addition, a class of polygamy inequalities has been obtained for multiqubit systems,

In Ref. [29], Kim established a class of tight monogamy inequalities of multiqubit entanglement in terms of Hamming weight. For any nonnegative integer j with binary expansion 

Kim proposed the tight constraints of multiqubit entanglement based on Hamming weights[29]




In the following we show that these inequalities above can be further improved to be much tighter under certain conditions, which provide tighter constraints on the multiqubit entanglement distribution.
We first present a class of tighter monogamy and polygamy inequalities of multiqubit entanglement in terms of the μ-th power of RαE. We need the following results.[32] Suppose k is a real number, 0 > k ≤1. Then for any 0≤ x ≤ k, we have

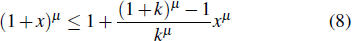
We first show that the inequality (


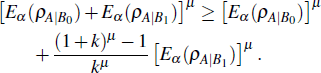
We assume that the inequality (

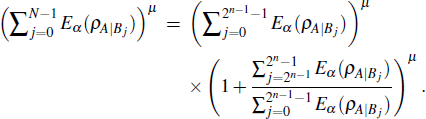

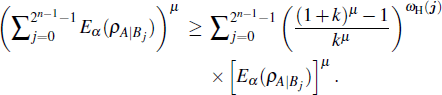

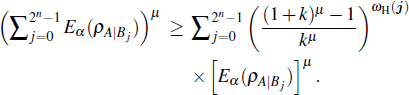
Now consider a (2n + 1)-qubit state

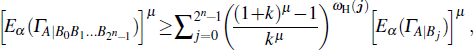

Since 

In fact, the tighter monogamy inequality (


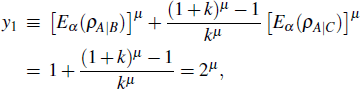
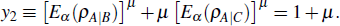
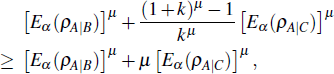
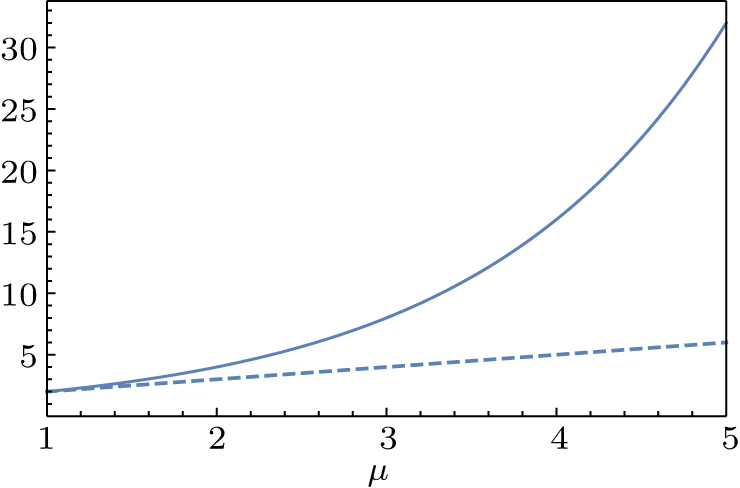 | Fig. 1. Rényi-α entanglement with respect to μ: the solid line is for y1 and the dashed line for y2 from the result in Ref. [29]. |
Under certain conditions, the inequality (
For any multiqubit state ρAB0… BN – 1, it is easy to show that
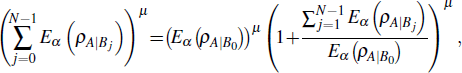

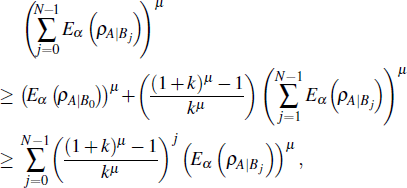
In fact, according to Eq. (
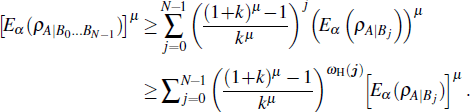
For the case of μ < 0, we can also derive a tighter upper bound of 
We consider now the RαEoA defined in Eq. (
Then we assume that the inequality (
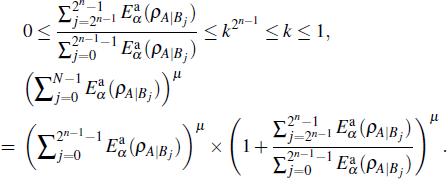
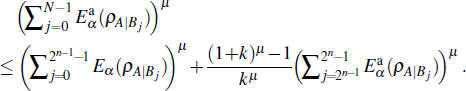
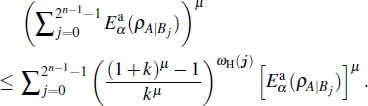

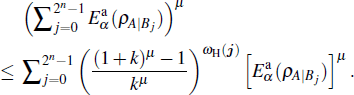

Since 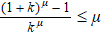
As an example, let us consider the three-qubit W-state[33]




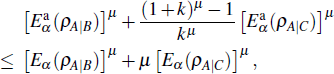
Similar to the improvement from the inequality (
Since ωH(j)≤ j, for 0≤μ≤1 we obtain
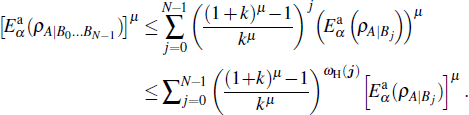
 | Fig. 2. Rényi-α entanglement y with respect to μ: the solid line is for y3 and the dashed line for y4 from the result in Ref. [29]. |
Quantum entanglement is the essential resource in quantum information. The monogamy and polygamy relations characterize the entanglement distributions in the multipartite systems. Tighter monogamy and polygamy inequalities give finer characterization of the entanglement distribution. In this article, by using the Hamming weights of binary vectors we have proposed a class of monogamy inequalities related to the μ-th power of the entanglement measure based on Rényi-α entropy, polygamy relations in terms of the μ-th powered of RαEoA for 0≤ μ ≤ 1. These new monogamy and polygamy relations are shown to be tighter than the existing ones. Moreover, it has been shown that our monogamy inequality is effective for the counterexamples of the CKW monogamy inequality in higher-dimensional systems. Our results may motivate further investigations on the entanglement distribution in multipartite systems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |

