† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11834005 and 11674285).
We study the single-photon transport in the coupled-resonator waveguide (CRW) controlled by an imperfect cavity. A Lorentzian spectrum is introduced to describe the dissipation. We find that the probability current conservation can be broken, although the imperfect cavity is a Hermitian system. The coupling strength between the imperfect cavity and the CRW has significant influences near the resonant frequency. With the increase of the coupling strength, the transmission coefficient becomes smaller. The spectral width plays a dominant role under the off-resonant condition, where the transmission coefficient is greatly suppressed with the increase of the spectral width. We also observe an abrupt jump of the transmission and reflection coefficients when the hopping amplitude is large enough. All the distinctive behaviors are closely related to the complex effective potential induced by the imperfect cavity.
Quantum optical switches are quantum systems to control the flow of light,[1–4] which play a significant role in the quantum circuits, quantum communication, and quantum networks.[5–8] One of the most notable quantum optical switches is based on the controllable scattering of a single photon in low-dimensional waveguides.[9,10] The waveguide transfers the photon which carries information, while the scattering center coupled to the waveguide serves as a switch to control the transmission and reflection of the photon.
Early studies mainly focus on the waveguide which is an one-dimensional continuum with linear dispersion.[9,11–16] Shen and Fan proposed a real-space Hamiltonian with which they predicted many novel properties of single photon transport, such as the general Fano line shape and symmetric vacuum Rabi splitting for a leaky cavity.[9] Recently, an one-dimensional coupled-resonator waveguide (CRW) with cosine-type dispersion gets more and more attention, which can be realized in the experiment by using superconducting transmission line resonators.[10] Due to the nonlinear dispersion relation, the reflection amplitude shows a more general structure, beyond the Breit–Wigner and Fano line shapes.[10] Two CRWs have been combined to study the quantum routing of single photon controlled by a cyclic three-level system.[17] Most recently, a dimerized CRW was proposed to study the scattering process which acts as a photonic analog of the Su–Schrieffer–Heeger model.[18,19] The dimerized CRW leads to unconventional scattering properties and different super- and sub-radiant states depending on the band topology.[18] Despite of the differences, all the waveguides mentioned above are Hermitian systems. The non-Hermitian waveguides with 
The scattering centers have much more choices than the waveguides. A single-mode cavity or resonator is one of the simplest scattering centers which can be direct or side coupled to the waveguide.[11,12] Besides, the interaction between them can be linear[14] or nonlinear.[23] Recent experiments have demonstrated that the light–matter interaction can reach ultrastrong and even deep-strong coupling regimes,[13,24,25] which make the multi-level atom or superconducting qubit a good candidate to be the scattering center.[1,9,10,26,27] Additionally, a two-level atom can be embedded in a cavity, while the cavity is coupled to the waveguide.[14,15] The hybrid atom-optomechanical systems can also be regarded as the scattering center, which reveal richer spectral features.[28–31]
Due to the influence of the environment, it is hard to construct a perfect single-mode cavity with no dissipation.[32] In the previous studies, one usually introduces an imaginary value to the cavity frequency to account for the dissipation,[14,15,29,31,33] which forms a non-Hermitian scattering center. For the non-Hermitian scattering center, the probability current is usually not conserved. However, a 
As shown in Fig.


The 0-th resonator is coupled with an additional cavity which serves as the scattering center. Here we consider two kinds of cavities: a perfect single-mode cavity and an imperfect cavity which introduces the influence of the environment-induced dissipation.
If the 0-th resonator of the 1D CRW is coupled to a perfect single-mode cavity, then the Hamiltonian under the rotating wave approximation can be written as


If the 0-th resonator of the 1D CRW is coupled to an imperfect cavity, then the corresponding Hamiltonian[32,39–42] would be

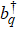



Here we focus on the single-photon elastic scattering. The stationary eigenstate corresponding to momentum k is assumed to be




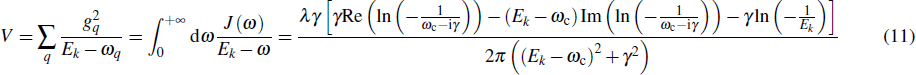
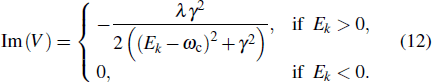
A photon with momentum k ∈ (0, π) incident from the left side of the CRW will result in transmitted and reflected photon. For j ≠ 0,
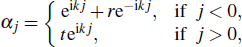
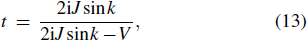
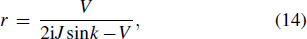


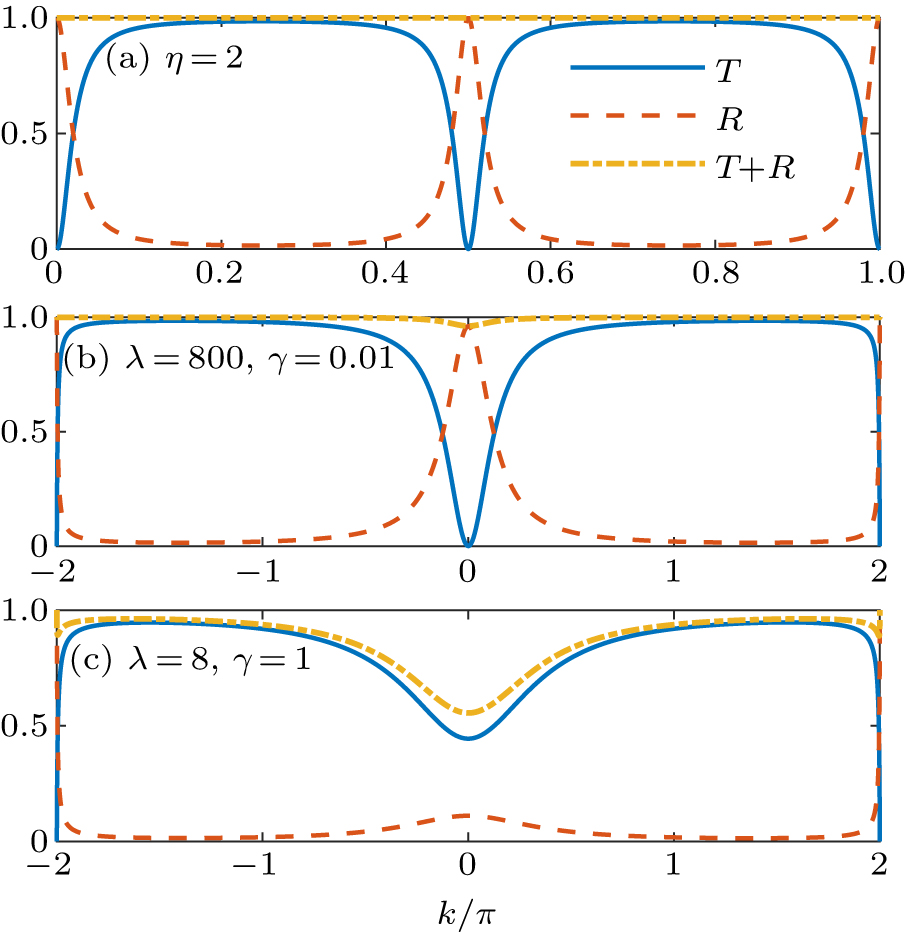
The imperfect cavity introduces the influence of dissipation on the perfect cavity. We expect that the imperfect cavity can recover the perfect one in the limit of weak dissipation γ → 0. According to the definition of the Dirac delta function



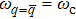
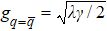
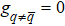

Figure 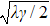
For the Hermitian scattering center, such as the two-level system, perfect cavity, et al.,[10,23] it usually satisfies T + R = 1, which is a signature of probability current conservation. The incident photon can either transmit through the scattering center or be reflected by it. The non-Hermitian scattering center introduces loss and gain, which can break the probability current conservation, except for some 
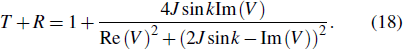
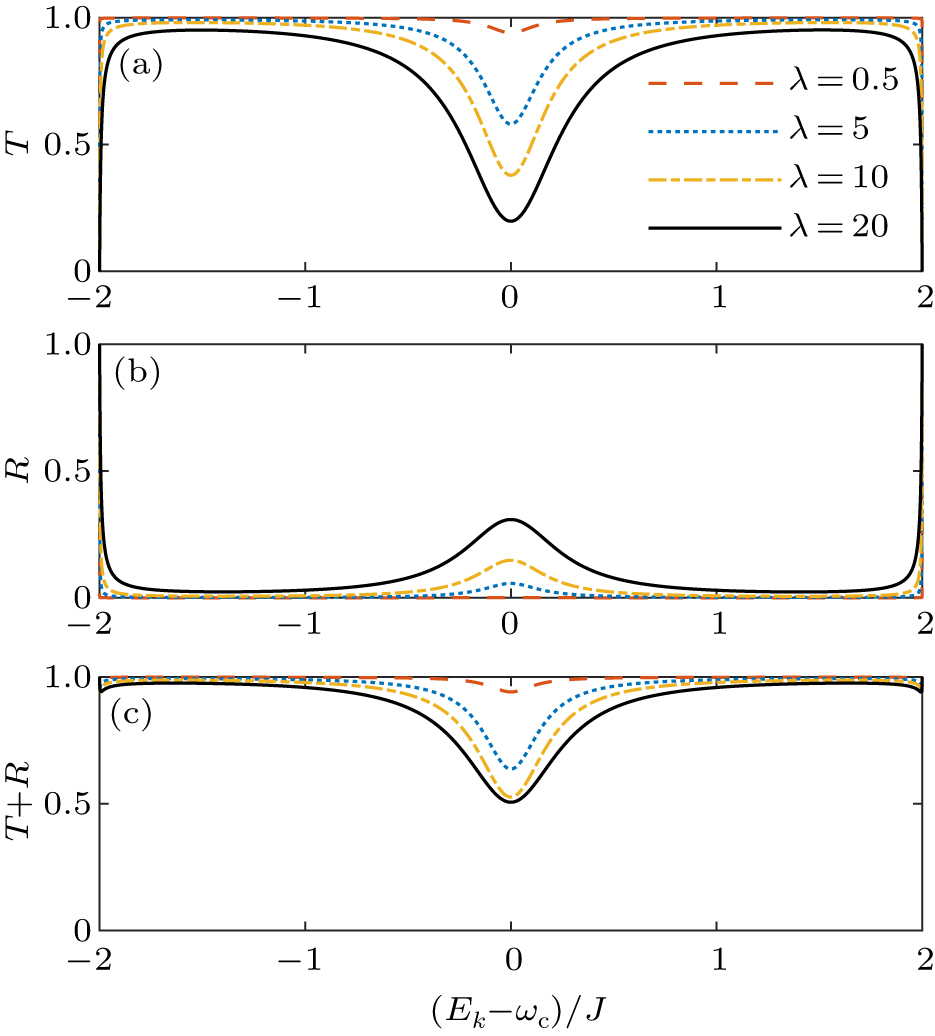
To further understand the influence of the imperfect cavity on the scattering process, we firstly plot the transmission and reflection coefficients for different coupling strength λ, as shown in Fig.
We then plot the transmission and reflection coefficients for different spectral width γ, as shown in Fig.

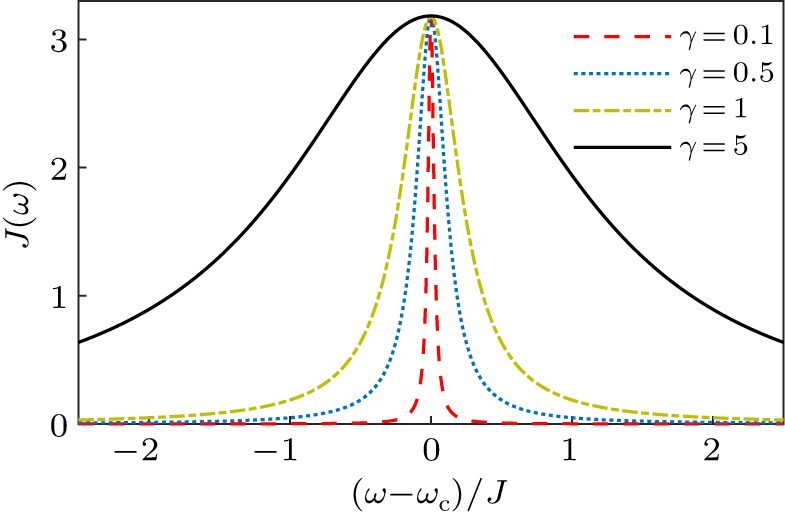 | Fig. 5. The spectral density J(ω) as a function of ω at ωc = 10, λ = 20 for γ = 0.1 (red dashed), 0.5 (blue dotted), 1 (yellow dash-dot), and 5 (black solid). |
A perfect cavity coupled with the 1D CRW is a good candidate to be the quantum optical switch.[10] It can be either a perfect mirror at the resonant frequency which totally reflects photons, or an ideal transparent medium far away from the resonant frequency which allows photons to pass. However, no cavities are perfect due to the environment-induced dissipation in the experiments. Our studies on the imperfect cavity indicate that a large coupling strength λ is necessary to maintain the high reflection coefficient at the resonant frequency as shown in Fig.
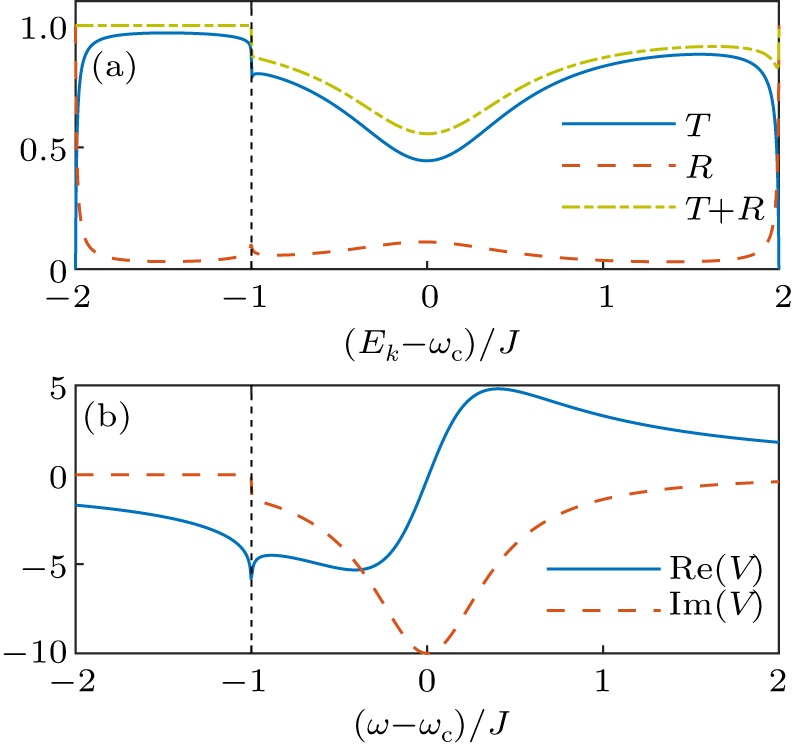
The influence of the hopping amplitude J on the transmission and reflection also deserves some attention. The range of Ek ∈ [Ω – 2J,Ω + 2J] increases with the increase of J. One can expect that increasing J can lead to larger detuning |Ek – ωc| which enhances the transmission but suppresses the reflection. One should also note that when J < Ω/2, Ek can be negative which leads to the disappear of the imaginary part of the effective potential (
We study the coherent transport of a single photon in a CRW. An imperfect cavity is coupled to the CRW which serves as the scattering center to control the transmission and reflection of the incident photon. The dissipation is taken into account by assuming a Lorentzian spectrum for the cavity. In the weak dissipation limit, the imperfect cavity recovers the behavior of the perfect one. For a finite dissipation, we find that the probability current conservation can be broken, even if it is a Hermitian system. The incident photon cannot only be reflected or transmitted, but also be kept in the imperfect cavity.
The coupling strength γ between the imperfect cavity and the CRW has significant influences on the scattering process, especially near the resonant frequency Ek ≃ ωc. With the increase of the coupling strength, the transmission coefficient becomes smaller while the reflection coefficient becomes larger. Besides, their summation becomes smaller as the incident photon has more probability to be kept in the imperfect cavity. The spectral width γ plays a dominant role under the off-resonant condition, where the transmission (reflection) coefficient is greatly suppressed (enhanced) with the increase of γ. It becomes very robust against the change of γ at the resonant frequency. To make the imperfect cavity a valid quantum optical switch, one needs to increase the coupling strength and decrease the spectral width.
We also observe a discontinuity of the transmission and reflection coefficients. When the hopping amplitude J of the CRW is large enough, the energy of the incident photon can be either positive or negative and the consequent scattering by the cavity varies greatly. The imperfect cavity induces a complex effective potential, which is closely related to all the observed phenomena.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] |