† Corresponding author. E-mail:
Project supported by the National Key Scientific Instrument and Equipment Development Project of China (Grant No. 2014YQ030975).
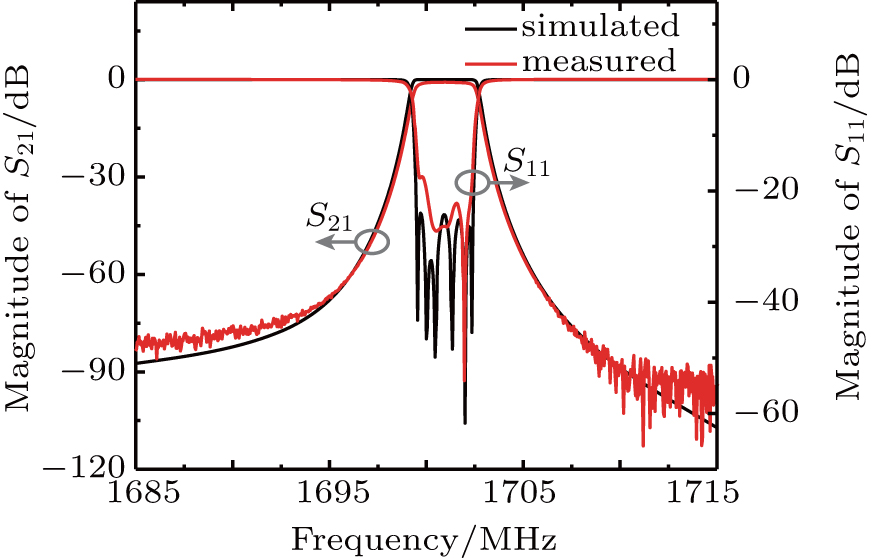
A novel N-spiral resonator with open-loop secondary coupling structure (OLSCS) is proposed to realize a compact ultra-narrowband high temperature superconducting (HTS) filter. The coupling strength and polarity between the resonators can be significantly reduced and changed by introducing OLSCS, thus the required weak coupling can be achieved in a very compact size. A six-pole superconducting filter at 1701 MHz with a fractional bandwidth of 0.19% is designed to validate this method. The filter is fabricated on MgO substrate with a compact size of 15 mm × 10 mm. The measured insertion loss is 0.79 dB, and the return loss is better than 17.4 dB. The experimental results show a good agreement with the simulations.
In the current wireless communication scenario, the development of innovative hardwire devices is necessary to support the rapid growth of new functions and complex services. Modern microwave structures have to satisfy increasingly stringent requirements for their performance, as well as compactness and ease of integration with other systems. The ultra-narrow bandpass filter has the advantage of improving the utilization of spectrum resources and system sensitivity, which plays an important role in microwave communication and detection systems. Since the insertion loss of a bandpass filter of a given order is inversely proportional to its fractional bandwidth (FBW),[1] it is difficult to achieve the ultra-narrowband filters using normal metals (especially FBW < 1%). Compared with normal metal conductors, superconducting thin films have extremely low microwave surface resistance, which help high temperature superconducting (HTS) microstrip resonators present very high quality factors (> 104)[1] and consequently make possible the fabrication of compact ultra-narrowband filters with high performances in terms of very low insertion in-band loss, high out-of-band rejection, and high selectivity.
For a given application, the miniaturization of an HTS ultra-narrowband filter is one of the most important research issues since it reduces the cost related to the necessary superconducting area, relaxes the cryogenic burden for the cryo-cooler, and facilitate the integration with other systems. Miniaturization requires the resonators in a filter to be in weak coupling conditions with small distances, and people have made great efforts to achieve that. Resonator design is a very important point for compact filter construction. Various resonator structures have been employed to develop compact HTS ultra-narrowband filters in recent years. Li and Huang et al.[2] proposed a multiloop resonator to design a quasi-elliptic filter with an FBW of 0.23%. Li et al.[3,4] presented a clip-shape resonator and a dual-spiral resonator to design quasi-elliptic function ultra-narrowband HTS filters with FBWs of 0.02% and 0.35%. Huang et al.[5] designed a resonator consisting of a microstrip spiral, with a reversal in winding direction and developed a 0.1% bandwidth filter. In addition, stepped impedance resonators are widely used in ultra-narrowband filters design.[6–8] Kawaguchi et al.[6] developed a quasi-elliptic filter with an FBW of 0.25% using stepped impedance resonators and separation filter package. Kwak et al.[7] presented a filter with a bandwidth of 17 MHz and a center frequency of 1760 MHz using meander line resonators with stepped impedance structures. Jin et al.[8] proposed a stepped impedance spiral resonator and developed an HTS filter with a bandwidth of 0.3%. Twin-spiral and twin spiral-in-spiral-out resonators have been employed to design filter with ultra-narrow bandwidth.[9–16] Tao et al. proposed modified twin-spiral and twin spiral-in-spiral-out resonators to realize weak couplings and designed two compact ultra-narrowband filters with FBWs of 0.08%[12] and 0.18%[14] in S band. Moreover, another inspiring method that adding secondary coupling structures between resonators to reduce coupling has also been investigated.[10,17] Lu et al.[10] presented a double U-type secondary coupling structure to reduce the coupling between twin-spiral resonators and realize a filter at 600 MHz with an FBW of 0.083%. Among the previous reports, bandwidth and compactness are often not well balanced, and the miniaturization of ultra-narrowband filters is still a challenging problem.
In this paper, in order to achieve a very compact ultra-narrowband filter configuration, we propose a novel N-spiral resonator surrounded by an open-loop secondary coupling structure (OLSCS). By introducing OLSCS, the coupling strength and polarity can be effectively weakened and controlled artificially. Consequently, a sufficiently weak coupling is obtained within a relatively small coupling distance. Furthermore, the interaction between OLSCS and N-spiral resonator, and the effect of OLSCS on the coupling are investigated and discussed. A six-pole ultra-narrowband filter with an FBW of 0.19% in L band is designed and fabricated to validate this method.
To realize a miniaturized ultra-narrowband filter, novel resonators with compact structures and weak coupling characteristics need to be satisfied. Figure
Figure
Figure
There is a capacitive coupling between the OLSCS and N-spiral resonator, resulting in a reduction in electric coupling. To explain the interaction between OLSCS and N-spiral resonator, as well as understand the effect of OLSCS on coupling, the coupled resonators are represented with a lumped element equivalent circuit as shown in Fig.
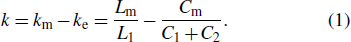
The contribution of OLSCS is contained in the expression of electric coupling coefficient above. It demonstrates that the electric coupling decreases as the capacitive coupling increases. When the electric coupling is reduced to less than the magnetic coupling, the magnetic coupling will become dominant between the coupled resonators. Therefore, when the electric coupling is weakened to be close to the magnetic coupling, very weak coupling can be realized using N-spiral resonators and OLSCSs without large resonator distance.
 | Fig. 3. (a) Charge density distribution of coupled N-spiral resonators with OLSCSs. (b) The equivalent circuit. |
The effect of the OLSCS on the coupling is simulated and shown in Fig.
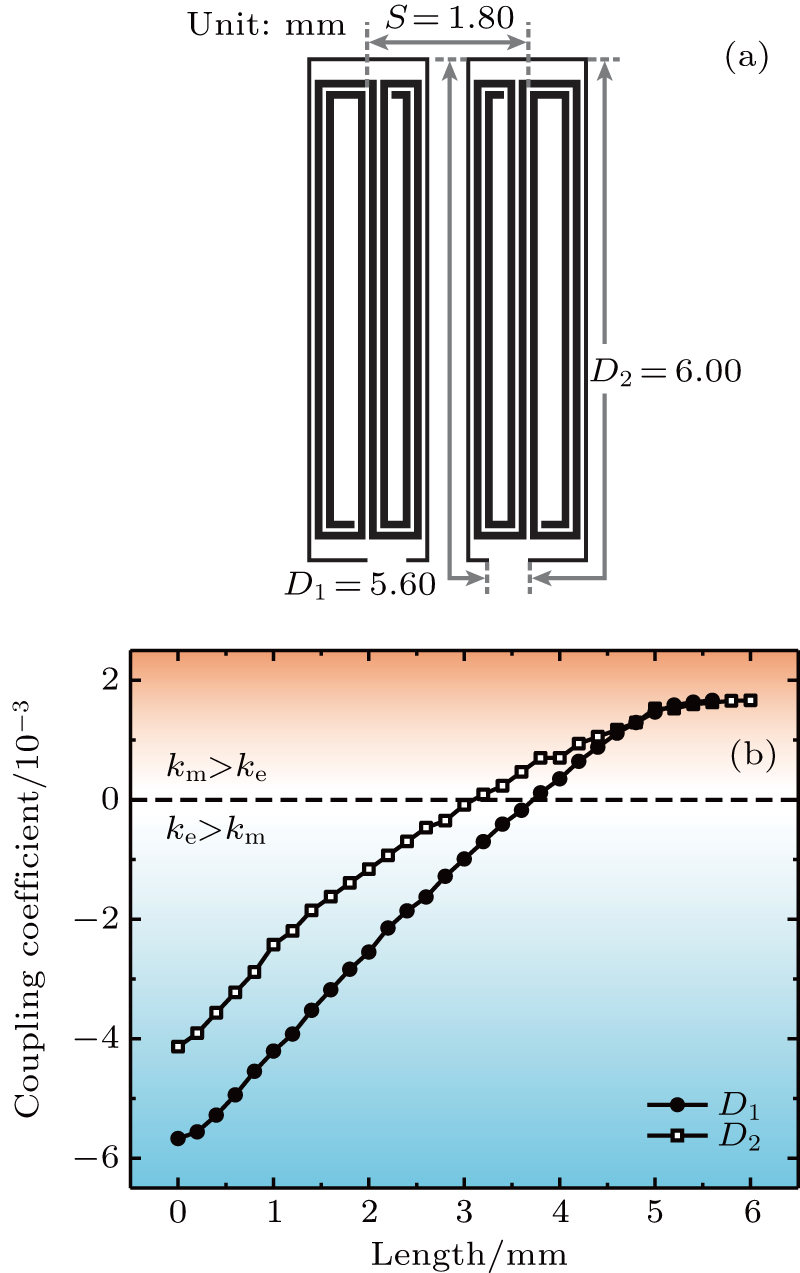 | Fig. 4. (a) Coupled N-spiral resonators with OLSCSs (S = 1.80 mm, D1 = 5.60 mm, D2 = 6.00 mm). (b) Coupling coefficient versus the lengths of D1 and D2 of the OLSCSs (S = 1.80 mm). |
In order to identify the influence of OLSCS, we investigate the coupling behavior in the modified N-spiral resonator shown in Fig.
The coupling strengths between N-spiral resonators with and without OLSCSs are compared in Fig.
 | Fig. 6. The coupling strengths between N-spiral resonators with and without OLSCSs as a function of the resonator center distance S. |
The capacitive coupling between the OLSCS and the N-spiral resonator will pull down the resonator frequency, which is a critical issue for ultra-narrowband filter design. To eliminate the effect of resonant frequency shift, the OLSCS and the N-spiral resonator are considered as a whole resonant element to facilitate the filter design.
A six-pole ultra-narrowband HTS filter with an FBW of 0.19% at 1701 MHz is designed using the N-spiral resonator with OLSCS to have a Chebyshev response.[1] The required coupling coefficients kij, (i = 1, …, 5, j = i + 1), and external quality factors Qe are determined as

 | Fig. 7. (a) Configuration of the feeding structure. (b) External quality factor Qe versus D6 and D7. |
Figure
Table
| Table 1. Comparison of the proposed filter with other reported filters. . |
In this paper, we proposed a novel N-spiral resonator with open-loop secondary coupling structure (OLSCS) to design a compact ultra-narrowband filter. The capacitive coupling between OLSCS and N-spiral resonator leads to the reduction of electric coupling. As the coupling between the N-spiral resonators without OLSCSs is mixed electromagnetic coupling and dominant by electric coupling, the coupling strength can be effectively reduced by introducing OLSCS, as well as the polarity can be changed to magnetic coupling with a transition zero point. Therefore, the required weak coupling can be achieved without large resonator distance using N-spiral resonator with OLSCS, which realizes the miniaturization. To demonstrate the novel structure, a six-pole HTS ultra-narrowband filter with an FBW of 0.19% has been designed and fabricated in a compact size of 15 mm × 10 mm. The measured results show a good agreement with the simulations.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |