† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51572143, 51822206, and 51932010).
The electronic structures of lead-free piezoceramic (K0.5Na0.5)NbO3 (KNN) and La-doped KNN ((K0.5Na0.5)0.994La0.006NbO3) are studied by using first principles calculation on the basis of density functional theory (DFT). The results reveale that the piezoelectricity stems from strong hybridization between the Nb atom and the O atom. At the same time, the K or Na atoms are replaced by the La doping atoms, which brings about the anisotropic relaxation. The La doping reduces the forbidden band, at the same time it makes Fermi surfaces shift toward the energetic conduction band (CB) of KNN. With the increase of La-doping intent, the phase structure of KNN extends from O-phase to T-phase and improves the piezoelectric properties of KNN.
Piezoelectric material is one of the important functional materials, which can realize the mutual conversion between mechanical energy and electrical energy, and has been widely used in modern industry and defense field. The macroscaled bulk piezoelectric materials can be used in underwater acoustic transducer, medical B-ultrasonic probe, ultrasonic motor, oil logging detector, non-destructive testing, and acceleration sensor, and so on.[1–5] At present, the further development of new bulk piezoelectric material system is one of the key research directions in the field of piezoelectric materials.[6]
For a long time, lead-based material, represented by lead zirconate titanate (PZT), has attracted more and more attention because of its outstanding piezoelectric, electromechanical and dielectric properties. Based on this kind of piezoelectric material, the sensors, transducers, and other devices have been used in engineering. However, there are still many dangerous factors from the main ingredient in PZT. Due to the toxicity of lead, the preparation, use and disposal of lead-based piezoelectric materials will be harmful to human body and the environment. To adapt sustainable development strategies, there is a need to end the use of plumbum and synthesize lead-free piezoelectric ceramics systems which can be applied to green technology and be environmentally friendly. In view of the harmfulness of lead-based piezoelectric material, it is a crucial and urgent task to develop new lead-free piezoelectric ceramic materials. According to previous research, numerous lead-free ceramic systems can be produced, such as BaTiO3, (K,Na)NbO3 (KNN), and (Bi,Na)TiO3 based ceramics.[7–9] But in recent years, the new potassium sodium niobate based bulk piezoelectric materials are considered to be the most promising lead-free piezoelectric material system due to their excellent electric performances, high Curie temperature.[10–13] Actually, one thinks that the polymorphic phase boundary (PPB) is a critical component of KNN-based piezoelectric material. With the composition near PPB of KNN-based ceramics, we can obtain outstanding piezoelectric properties.
According to some previous researches, donor doping in the KNN may induce the PPB’s production and could improve the piezoelectric property of KNN-based ceramics. For instance, the piezoelectric coefficient d33 of the ceramics can be enhanced obviously from 220 pC⋅N−1 to 274 pC⋅N−1–710 pC⋅N−1 after being doped with the donor ions Bi3+, La3+, and Nb5+. The La2O3, CeO2, and other lanthanide oxides have acted as donor dopants or additives in the BNT-based and BaTiO3-based unleaded piezoceramics, and have achieved good effects.[14,15]
But these achievements usually focus on experiments, but not on theoretical studies. Traditional experiments show that the piezoelectric property of KNN can be improved mostly through doping. This supports us to ascertain the doping mechanisms and influences on piezoelectric property from an atomic perspective.
First-principles calculations based on density functional theory (DFT) have gradually shown their importance in the study of the physical mechanism of materials in recent years. This method does not need relying on any empirical parameters. By purely solving the material’s intrinsic quantum mechanical equations, one can obtain the atomic, electronic structure and related physical properties of the material, and thus presenting a method of studying the relationship between the microstructure and macroscopic properties of materials. This method does not need to worry about the influence caused by the characterization test and data processing in the experiment. It can intuitively and effectively observe the local atomic structure, electronic structure, and system energy of the material, and give a corresponding physical explanation for the change of the performance of material. For example, by comparing and calculating the electronic structures of PbTiO3 and BaTiO3, the researchers found that the ferroelectricity of these two materials originates from the hybridization of the 3d orbital of Ti and the 2p orbital of O, and the difference in ferroelectric behavior between the two is due to the strong hybridization between 6s and O 2p in Pb, but Ba shows almost complete ionicity in BaTiO3.
Tan et al.[16] directly compared the piezoelectric properties of single crystals of KNbO3 (KN) and K0.5Na0.5NbO3 (KNN) with ceramics through the first-principles method and orientation averaging method, and found that the KNN ceramics has obviously higher piezoelectric performance than KN, comparing with KN, d33 is increased by about 70%, which is consistent with experimental observations, while the d33 mainly comes from the contributions of d15 and d33 in the single crystal. Further research found that the Born effective charges of the two are not much different from each other, but the large ion displacement caused by the smaller radius of Na can enhance ferroelectricity; at the same time, Na also causes the ion displacement of itself and adjacent O with strain response to be increased significantly, this is what causes higher piezoelectricity in KNN. Peng et al.[17] used the first-principles calculation method to calculate the elasticity and piezoelectric coefficients of orthogonal phase KNN at different Na concentrations, and reasonably estimated the piezoelectric coefficients of ceramics by using the orientation average method. It was found that when the Na content was 0.5625, the highest piezoelectric performance, the d33 of the ceramic can reach 88.6 pC/N. The study found that the orientation dependence of piezoelectric properties of single crystals is extremely sensitive to the change in the concentration of Na, and high shear piezoelectric moduli d15 and d24 have a strong relationship with the piezoelectric properties of enhanced polycrystalline KNN ceramics. Li et al.[18] used DFT combined with VCA method to study the piezoelectric coefficient of K1–xNaxNbO3 system in detail, and predicted the components of morphotropic phase boundary (MPB). At the same time, the structural parameters, bulk modulus, and forbidden band width of the system were calculated, and it was pointed out that when x = 0.5, its polarization direction of intensity turned from [011] to [001] to have lower energy barriers than that the pure KNbO3 has, and this results in the enhanced piezoelectric characteristics.
What is studied in this paper is the electronic structure of (K0.5Na0.5)NbO3 and La-doped (K0.5Na0.5)NbO3 lead-free piezoceramics through first principles calculations on the basis of DFT.
It is found that the main contribution to enhanced piezoelectricity of La-doped KNN is the hybridization of O 2p and Nb 4d orbitals. The relative mechanism is also discussed.
We believe that this research can provide the necessary theoretical basis for its practical application.
In this study, the density functional theory (DFT) calculation was conducted with the Vienna ab-initio simulation package.[19] The electron–ion interaction was described by projector augmented-wave (PAW) pseudopotential. In the exchange and correlation functional, the Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) exchance–correlation was applied.[20,21] In the DFT calculation, the kinetic energy cutoff of 520 eV was used for the wave functions expansion. Brillouin zone integration was conducted on the grid with 2 × 2 × 2 for geometry optimization and 4 × 4 × 4 k-grid mesh for calculation of density of states. To calculate the electronic structure of K0.5Na0.5NbO3, we used the unit cell lattice that has a = b = 3.996 and c = 4.063 in the tetragonal phase to build a supercell in the [001] direction for K0.5Na0.5NbO3 as shown in Fig.
The perturbed angular correlation (PAC) is the basis of hyperfine interaction (HFI). The PAC supplies an uncommon method to investigate the piezoelectric material’s electric performances by the electric field gradient (EFG) extracted from the measuring HFI. Tables
| Table 1. Comparison of coordination between La-doped KNN and undoped KNN. . |
For the diverse atom sites, the bond distances are obtained at the force of no more than 0.01 eV⋅Å−1. As can be seen from Table
| Table 2. EFG of (K0.5Na0.5)NbO3 and La-doped (K0.5Na0.5)NbO3. . |
The main part of EFG tensor is in the orientation of [001] which has an asymmetric parameter of η = 0. As can be seen from Table
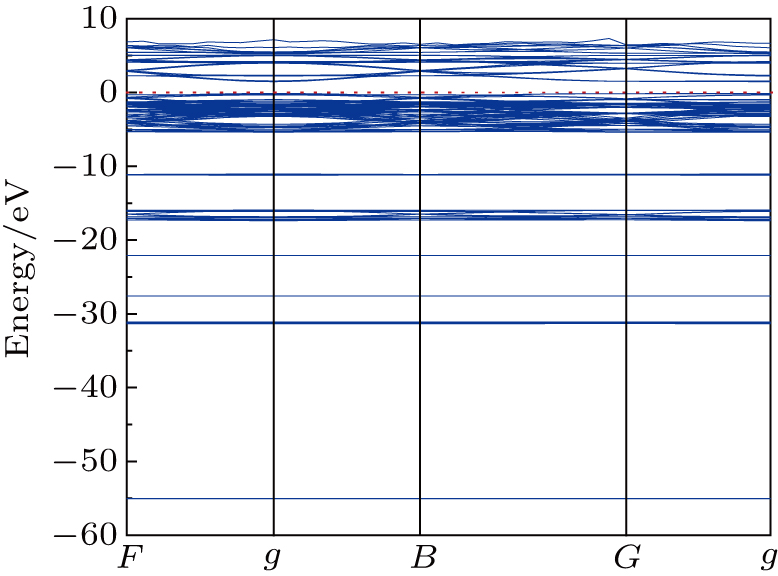
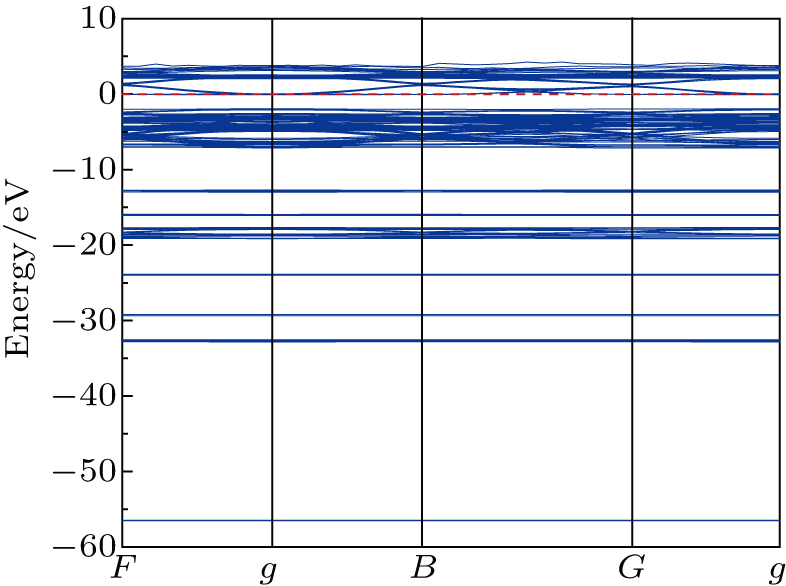
For calculating the band structure, we employ a k-point route along the F–g–B–G–g points of the symmetry. Figure
Figure
Figure
According to Figs.
The formation energy is the energy that is required when doping atoms substitute for replaced atom. When the formation energy is weaker, the doping atom enters into lattice location more easily. We calculate formation energy of La atom when it replaces K and Na atoms in KNN separately.
Here is the formula for doping formation energy, the formation energy (ΔEformation) is defined as follows:

The formation energy of the substituted atom La is shown in Table
| Table 3. Calculated formation energy (in unit eV). . |
We investigated the electronic structures of the lead-free piezoceramics (K0.5Na0.5)NbO3 and the La modified (K0.5Na0.5)NbO3 by the first principles calculations. The calculations prove that the La-doping reduces the energy gap and makes Fermi surface to shift toward high-energy CB, and K and La atoms can substitute for Na atom more easily. La doping leads to anisotropic relaxation. This is the main reason for the lowering of the phase transition temperature from the orthorhombic to the tetragonal phase or the change of the lattice structure to the tetragonal phase. This can improve the piezoelectric property of KNN. At the same time, we calculate the EFG, band structure, total DOS, and fractional DOS. It can be confirmed that the main contribution to piezoelectricity is from the hybridization of O-2p and Nb-4d orbitals. This makes the Nb–O octahedron distorted. And it is a probable method to improve the piezoelectricity of KNN materials.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |