Recently, it is under debate whether the half-quantized conductance plateau could be used as an evidence for chiral Majorana modes in a millimeter-size quantum anomalous Hall–niobium hybrid device.^[1,2] As a symmetric solution for the Dirac equation, Majorana fermion is its own antiparticle.^[3,4] In solid-state physics, Majorana fermionic quasi-particle produces a zero-energy mode (ZEM), which is present in differential conductance and spectral density functions.^[5–9] The Majorana ZEM has some remarkable physical properties that could lead to advances in quantum computing.^[10–12] ZEMs have received considerable attention owing to their special performance. Ferreira et al. have studied ZEMs resilient to localization in graphene subjected to chiral-symmetric disorder and reported accurate quantum transport calculations. Ganeshan et al. have determined that the commensurate off-diagonal Aubry–André or Harper models support ZEMs. Fan et al. have proposed ZEMs and tunable electronic band gap in periodic heterosubstrate-induced graphene superlattices.^[13]

Quantum dot (QD), which is also referred to as an artificial atom, is a small structure with electrons that are restricted in all three dimensions. It is convenient to study quantum phenomena in QDs, particularly those with many-body properties, which are vital for miniaturizing electronic devices.^[14,15] Double quantum dots (DQDs), which are frequently used in laboratory experiments,^[16–18] have a simple configuration that allows to study the effects of inter-dot interactions. In this study, we adopt hierarchical equations of motion (HEOM) to calculate the spectra of symmetrically serially coupled DQD. We propose a novel ZEM which occurs at finite temperature (approximately 7.5Δ, Δ is the hybridization of the QD system and electron reservoir, see details in next section). Owing to accessible temperature, this ZEM is easy to achieve, and the corresponding quasi-particle may provide another candidate for quantum computation.

The paper is arranged as follows. First, we introduce the HEOM numerical method. Then, we report the characters and parameters of ZEM using a simple explanation. Finally, we present conclusions and expectations.

By using the time derivative path integral influence functional expression,^[19–24] the HEOM approach allows to address open systems. On the basis of the linear response theory of quantum open systems,^[25] HEOM can accurately and efficiently produce the dynamical observables of strongly correlated quantum impurity systems.^[26] The total Hamiltonian can be regarded as the system-plus-reservoir composite, H_total = H_sys + H_res + H_sys-res. We consider a coupled DQD described by the Anderson impurity model, where the system Hamiltonian H_sys is

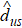
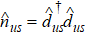
We treat the reservoirs as a bath environment. The Hamiltonian is written as

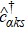
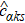
In this study, we consider a serially coupled DQD for which the coupling Hamiltonian is written as

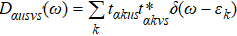
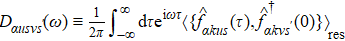
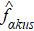
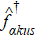
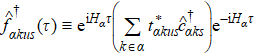
HEOM has a universal formalism for an arbitrary system Hamiltonian; the coupled DQD we choose in this study is an application. The form of the HEOM formalism reads

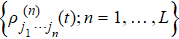
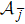
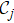
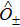
The HEOM formalism, Eq. (4), is exact for arbitrary Fermion reservoirs that satisfy Gaussian statistics.^[19,27,28] The HEOM evaluation of such spectral density system has been well-established, which is also nonperturbative.^{[19,26,29,30]}

Numerically, because the maximum hierarchical level for the full HEOM theory is difficult in practice, we adopt the Padé spectrum decomposition (PSD) scheme^[31,32] to minimize the computational expenditure while maintaining the quantitative accuracy. We determine that a relatively low truncation tier level is sufficient to yield quantitatively converged results for this system–reservoir coupling.^[26] In this work, the truncation tier L = 4.

For the dynamical quantities, the correlation function is described by the difference between t_A and t_B, where and are two arbitrary operators of the system in the Heisenberg picture. According to the definition, we have , where the operators and the thermal equilibrium density operator are defined in the total space.

HEOM numerical evaluation focuses on the reduced system density [cf. Eq. (4)] which includes the influence of the reservoirs at every tier. Thus, we retrieve . By applying the Fourier transform and , we can obtain the correlation function in reduced system in the frequency domain. Specifically, set and , the correlation function is reduced to Green's function , where is the annihilation (creation) operator of an electron in the system marked by μ, μ ≡ (us).

Therefore, QD1 and QD2 are equivalent to each other and symmetrically serially coupled to reservoirs L and R, respectively. We write G_s(ω) = G_1s(ω) = G_2s(ω) and omit the subscript s at spin degeneracy so that the spectral density function is written as .

In this work, we focus on the equilibrium scenario where μ_L = μ_R = 0. We also set Δ_L1s = Δ_R2s = Δ, and use Δ as the unit of energy.

For DQD, at extremely low temperatures (T ≪ T_K, T_K is the Kondo temperature of individual QD),^[33,34] the nonzero t produces an effective anti-ferromagnetic coupling, J = 4t²/U, between the local spin moments on both QDs.^[35] When J is weak, the two spin moments are almost independent of each other, and itinerant electrons separately screen the local spin at each QD. Thus, we can observe one zero-energy peak in the spectral function A(ω), which is recognized as a many-body Kondo resonant peak.^[26,36,37] In contrast, when J is sufficiently strong, spin-singlet states are formed, which span over both impurities. Then, the zero-energy peak will split into two.^[26,36] At the low temperature of approximately T ∼ T_K, the Kondo effect remains dominant but cannot fully develop owing to the finite temperature.^[34]

At medium temperature T ≫ T_K, we observe another ZEM, which indicates a new type of resonance processes other than the Kondo one. Using the HEOM method, we systematically study DQD [Eq. (3)], and the details are shown in Fig. 1.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Spectral functions A(ω) in coupled DQD, (a) at the medium temperature of T = 4.0Δ and specific intradot Coulomb coupling U = 7.5Δ with various tunneling coupling t; (b) at specific effective anti-ferromagnetic energy J = 3.5Δ at various temperatures T; (c) at the medium temperature of T = 4.0Δ and specific t = 3.0Δ with various U; (d) at the medium temperature of T = 4.0Δ and specific U = 7.5Δ, t = 3.0Δ with various hybridizations Δm. All parameters are in units of Δ = 0.2 meV.

By referring to Fig. 1(a), one can only see the Hubbard peaks at ω = ϵ_d and ϵ_d + U at small t. With an increase in t, the well-known Hubbard two-peak structure gradually changes into ZEM. This newly observed ZEM occurs at medium temperature (T ≫ T_K), which is related to the charge degree of freedom, as shown in Fig. 1(b). ZEM exists at a certain medium T (T = 5.0Δ) and will be destroyed when we tune T to a lower value (T = 2.0Δ). In addition, we test ZEM at different intradot Coulomb coupling U, as shown in Fig. 1(c). At t = 3.0Δ and T = 4.0Δ, U = 5.0Δ shows few characteristics of ZEM. It is known that larger U leads to lower T_K.^[34] With an increase in U, we do not expect the Kondo resonate peak to occur, and the results show another new ZEM. The height A(0) first increases. After it reaches the maximum, with a further increase in U, the new ZEM will be destroyed. This occurs at specific U, i.e., specific J. We observe that ZEM affects the reservoirs, limits the hybridization Δ in Fig. 1(d), and increases the height of A(0) in the vicinity of the Fermi level; however, the ZEM peak breaks up at weak Δ. ZEM at specific parameters presents as an excitation with a clear peak line shape, which can be regarded as a quasi-particle.

We observe that ZEM returns to the Hubbard two-peak structure at t, T, or U; however, the Hubbard two-peaks correspond to different ground states, for which we show the schematic of phase diagram in Fig. 2(a). At zero-T and zero-t limit, DQD is decoupled into two single QDs, and each localized spin moment is screened by itinerant electrons, which forms a many-body Kondo singlet. In the spectral function A(ω), the Kondo singlet corresponds to the zero-energy peak with A(0)πΔ = 1.^[34] At the temperature below and the finite tunneling coupling t, the Kondo singlet state is dominant, and the Kondo zero-energy peak still exists.^[37] With a further increase in t, the interdot tunneling effect will be bound to the two single spin-1/2 moments in each QD with a spin singlet.^[26,36] One can observe the splitting of the Kondo peak in A(ω). For the medium temperature scenario, weak-t affects the free moments with the active charge degree of freedom, which corresponds to A(ω) functions in Fig. 1(a) at t < 1.0Δ, and Fig. 1(c) at U ≈ 5.0Δ. At another limit T > T_st with strong-t, which corresponds to strong-J in DQDs, the ground state is known as a spin triplet,^[36] where T_st is the transition temperature of the spin singlet and triplet.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Energy levels in an isolate DQD with tuning t. (b) Schematic of temperature T–the interdot tunneling coupling t phase diagram of DQDs coupled to reservoirs.

We further analyze the mechanism of ZEM from an energy-level view illustrated in Fig. 2(a) and consider that the energy levels of the coupled DQD do not affect the physics with or without the hybridization of reservoirs. We choose an isolate DQD with the same parameters as those of our target DQD, where U = –2ϵ_d = 7.5Δ. Let us focus on the lowest energy levels. The spin singlet level decreases as the square root of [(4t/U)²+1]. Meanwhile, the spin triplet level does not change when t increases. Starting at 2ϵ_d, the spin singlet level and spin triplet level are separated so that the exchange energy J increases. The single-electron level, which begins at ϵ_d, splits into the ϵ_d – t level for asymmetric composition and into the ϵ_d + t level for symmetric composition. Thus, the asymmetrically composed single-electron level will cross the spin triplet level at t = 1/2U, which provides a special degeneracy. We propose a reason for the newly observed ZEM at the interference of two levels at specific parameters.

In the t–T phase diagram of the coupled DQDs, the newly observed ZEM is schematically identified by the green marked position in Fig. 2(b). According to the analysis of numerical results in Fig. 1, we conclude that ZEM occurs at medium temperature, and specific t is stronger than that for the free moment phase and weaker than that for the spin triplet phase, which is shown in Fig. 2(b) with two transform tunneling couplings t₁ and t₂.

In this scenario with spin symmetry, between the cross levels, both electrons and holes have the same energy gap. Thus, in the ZEM regime, the reflection on spectral function A(ω) shows the symmetry of electrons and holes.

Both the asymmetrically composed single-electron level and the spin triplet level are sensitive to the magnetic field. We examine the scenario at the finite magnetic field B = 1.5μ_BΔ. For the energy levels in the isolate DQD, shown in Figs. 3(a) and 3(b), the single-electron level is split into two: one for spin up, which moves downward by 1/2μ_BB, and the other for spin down, which moves upward by the same amplitude. The spin triplet level is reduced into three levels: one for spin up downward to 2ϵ_d – μ_BB, one for spin down upward to 2ϵ_d + μ_BB, and the last one at 2ϵ_d as the symmetric composition of the other two. The energy levels provide a clear view to analyze the ZEM excitation at the finite magnetic field for both electron and hole types.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Energy levels in an isolated DQD at the finite magnetic field of B = 1.5μBΔ: (a) spin up, (b) spin down. Corresponding spectral functions at different t of (c) spin up and (d) spin down.

For the excitation of spin up, the energy levels in Fig. 3(a) marked by red, the electron excitation arrow maintains the same direction at the degeneracy point of the non-field case. However, the hole excitation arrow, which is marked by blue, is opposite. Thus, the entire spin up part shows an electron type. In contrast, for spin down, the hole excitation is dominant, and the entire spin down part changes into the hole type [cf. Fig. 3(b)]. We observe that the degree of freedom of charge is entangled with that of spin in the ZEM regime.

By tuning J via t, at medium temperature above T_st, we can observe a phase transition from the spin singlet regime into ZEM regime at finite magnetic field in spectral functions shown in Fig. 3(c) for spin up and Fig. 3(d) for spin down. The ZEM of the spin up part in Fig. 3(c) changes into an electron quasi-particle; meanwhile the spin down part changes into a hole quasi-particle. We propose that the magnetic field reduces the degeneracy of spin, which is entangled with charge, so that the magnetic field can split the ZEM peak in the spectra.

We adopt the HEOM formalism on a symmetrically coupled DQD. At the temperature above the spin singlet–triplet transition temperature, we propose a novel zero-energy mode, which arises from the resonance of electron quasi-particle and hole quasi-particle; this zero-energy mode shows a ZEM peak in the spectral function. By further examining the effect of the magnetic field, because the degrees of freedom of spin and charge are entangled, it is determined that the magnetic field can split ZEM in the spectra.

The new reported ZEM in symmetrically serially coupled DQD is available for the evaluation at finite temperature. Therefore, the new ZEM could be a potential quantum bit candidate for quantum calculations.