† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFE031300), the Key Program of Research and Development of Hefei Science Center of China (Grant No. 2017HSC-KPRD002), the National Natural Science Foundation of China (Grant No. 11805231), the Natural Science Foundation of Anhui Province of China (Grant Nos. 1908085J01, 1808085QA14, and 1908085QF274), the ASIPP Science and Research Fund of China (Grant No. DSJJ-17-03), Collaborative Innovation Program of Hefei Science Center, CAS (Grant No. 2019HSC-CIP005), and Anqing Normal University Research Project, China (Grant Nos. 043-180079 and 044-140001000024).
We report the measurement of total molybdenum ion density for L-mode and H-mode plasmas on EAST using spectral lines observation and calculation based on an impurity transport code. A flat-filed extreme ultraviolet spectrometer with some spatial resolution is used to obtain the radial profiles of molybdenum spectral line emissions. The absolute calibration for the extreme ultraviolet spectrometer is finished by comparing the calculated bremsstrahlung intensity with the readings of CCD detector. Molybdenum ion transport study is performed using the radial ion density profiles and one-dimensional impurity transport code STRAHL. The total molybdenum density profiles are determined from the transport analysis. The molybdenum density during L-mode and H-mode phases are obtained, which are about 3 and 4 orders of magnitude smaller than the electron density, respectively. An inward pinch is found during the H-mode phase that leads to the peaked profile of molybdenum density.
Research of the impurity behavior is important for tokamak plasma operations since the degradation of plasma performance can be avoided by controlling the impurity content in the core and the impurity radiation loss at the edge.[1] It has been observed that impurity profiles tend to be more peaked than the main ion profile in many experiments, which is known as the impurity accumulation.[2] Impurity accumulation is found to be more severe for heavier impurity species.[3] On the EAST tokamak, heavy impurity species are mainly from metal impurities such as iron, copper, molybdenum, and tungsten,[4] and impurity accumulation is often observed, especially during the high-density H-mode plasma operations.
Spectroscopy is a unique method to measure the impurity spectra and to study the impurity behavior. In particular, extreme ultraviolet (EUV) spectroscopy is an excellent tool for the impurity diagnostics in high-temperature plasmas of fusion devices.[5–10] A flat-filed grating spectrometer that utilizes varied line spacing gratings to image the spectrum of 5–50 nm was installed in the EAST tokamak to monitor core impurity emission profile for impurity transport investigations.[11] Absolute intensity calibration of the spectrometers was performed by using the bremsstrahlung continuum in ohmic discharges on EAST tokamak.[12] Experimental impurity transport investigations have been performed in many magnetic confinement devices and most of the impurity transport studies have been carried out using the spatial profiles of absolute intensities of spectral emissions from spectroscopic measurement and comparison with an impurity transport code to determine the transport coefficients.[13–18] A future reactor will use high-Z plasma facing components (PFCs) such as tungsten in order to provide low erosion, sputtering yield and tritium retention. Since 2012, the first wall material of EAST has been mostly changed into molybdenum, which makes molybdenum as the most commonly seen metal impurity. Molybdenum density measurement can be useful for the molybdenum behavior study and evaluation of its effect on plasma performance. Among the metallic impurities that can be used for transport study, molybdenum has a good and well assessed knowledge base of the atomic physics.
In the rest of this paper, the experimental setup and the observations of molybdenum spectral lines are presented first. Then the absolute value calibration for the EUV spectrometer is illustrated in Section
The experimental advanced superconducting tokamak (EAST) is the first fully superconducting tokamak dedicated to high-performance and long-pulse operation, with elongated divertor configuration (an elongation ratio κ < 1.9).[19] The tokamak has a major radius of R ∼ 1.85 m and a minor radius of a = 0.4–0.45 m. Now, the EAST is equipped with lower hybrid current drive (LHCD), ion cyclotron range of frequency (ICRF), neutral beam injection (NBI), and electron cyclotron resonance heating (ECRH) systems, as the main auxiliary heating and current drive systems. Upper divertors are mainly made up of tungsten and the first wall is composed of molybdenum, which constitute the main part of plasma facing materials (PFMs) on the EAST. The spatial profiles of molybdenum spectral lines are monitored using an EUV spectrometer, which consists of two main parts: an adjustable entrance slit with a width of 0–0.5 mm determining the spectral resolution and height at 0–1 mm controlling the space resolution, a varied-line-spacing (VLS) spherically concaved holographic grating, and a back-illuminated charge coupled device (CCD) detector. The EUV spectrometer is now installed at the EAST’s port C and is attached to the end of vacuum pumping duct. The optical layout of the spectrometer can be seen in Fig.
 | Fig. 1. Schematic drawing of space-resolved spectrometer (a) optical path in top view and (b) principle of spatial resolution in vertical view. |
Figure
Absolute intensity calibration for the EUV spectrometer is technically difficult due to the lack of appropriate standard light source in the EUV range. In this paper, the absolute intensity calibration is conducted by comparing the calculated bremsstrahlung intensity with the measured bremsstrahlung intensity in the EUV range.
The continuum radiation can be divided into bremsstrahlung and recombination radiation. In the present fusion plasma with high electron temperature, the contribution of recombination radiation is very small compared with bremsstrahlung. Therefore, in our case we only consider continuum radiation as the bremsstrahlung. The bremsstrahlung power can be expressed as[20]

Since the measured intensity of bremsstrahlung is presented by the counting rate of photons, equation (

Finally, the absolute intensity calibration of EUV spectrometer can be obtained by comparing the observed EUV bremsstrahlung radiation profile with the calculated EUV bremsstrahlung and the absolute intensity calibration factor can be expressed as

Ohmic discharges are chosen for calculating the bremsstrahlung intensity. The parameters of the discharge are Ip = 400 kA, Bt = 2 T, and Zeff = 3. The Gaunt factor is calculated with the code RADZ.[12] From 5.8 nm to 20.1 nm, the chosen wavelength intervals for absolute intensity calibration of the spectrometer are listed in Table
| Table 1. The chosen bremsstrahlung continuum wavelength intervals for absolute calibration of the EUV spectrometer. . |
| Table 2. Sensitivity calibration coefficients of the present EUV system. . |
The waveform of a typical EAST H-mode discharge together with the time evolution of Mo XXXI intensity at 11.59 nm is shown in Fig.
 | Fig. 3. The time evolution of shot 38300: (a) plasma current, (b) loop voltage, (c) Hα intensity, (d) LHCD power, (e) ICRF power, and (f) intensity of Mo XXXI (11.59 nm). |
 | Fig. 4. The intensity profiles of Mo XXX, Mo XXXI and Mo XXXII during L-mode (t = 2.4 s) and H-mode (t = 3.8 s) phases from shot 38300. |
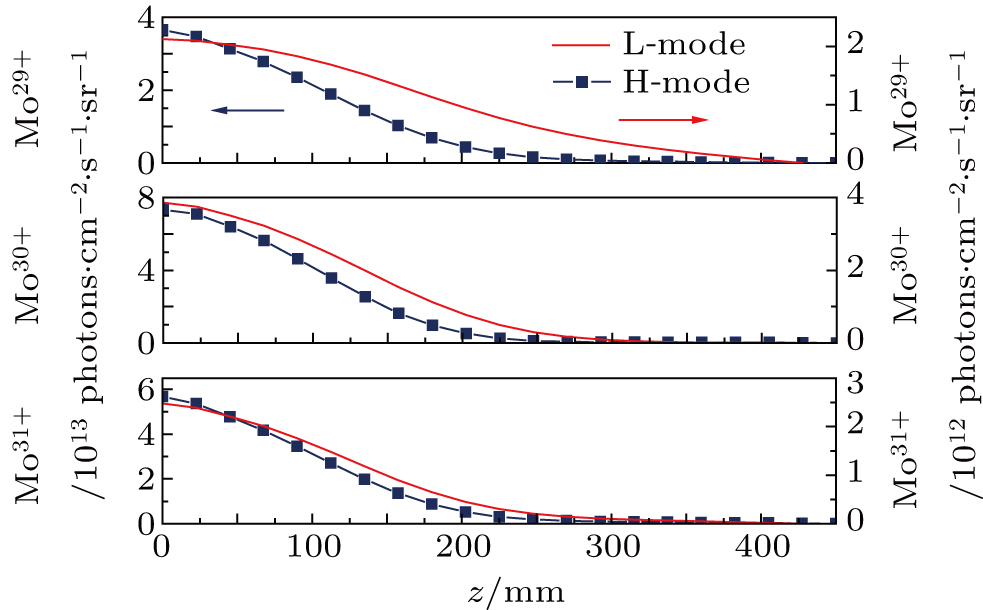 | Fig. 5. The chord-integrated brightness profiles of Mo XXX, Mo XXXI and Mo XXXII during L-mode (t = 2.4 s) and H-mode (t = 3.8 s) phases from shot 38300. |
The local radial emissivity profiles can be obtained using an Abel-like matrix inversion technique. The relationship between the line integrated brightness and the local emissivity can be expressed as[23]

The emissivity Ej can be obtained by inverting Eq. (

 | Fig. 6. The emissivity profiles of Mo XXX, Mo XXXI and Mo XXXII as a function of ρ during L-mode (t = 2.4 s) and H-mode (t = 3.8 es) phases from shot 38300. |
The emissivity of a particular transition from the initial state to the final state can be expressed as

The radial profile of Mo29+ spectral emission at 12.242 can be calculated by


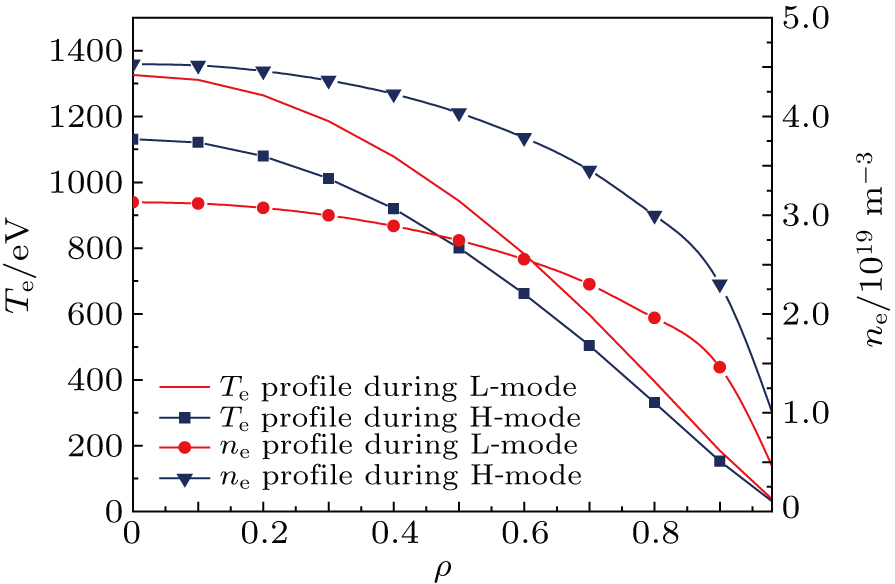
For Mo XXXI at 11.5988 nm and Mo XXXII at 12.7868 nm, the density profile can also be calculated in the same way as Mo XXX. The electron density and temperature are measured by Thomson scattering diagnostic and the profiles are shown in Fig.
In order to calculate the total molybdenum density, the molybdenum density’s radial profile has been computed using a 1D impurity code, STRAHL, and matched with the measured results.[25] The STRAHL code solves the coupled radial impurity transport equations for ions at all possible ionization stages. For one charge stage Z, the coupled radial impurity transport equation can be expressed as


Running of the STRAHL code starts with initial guesses of diffusion and convective coefficients to compute the impurity radial profiles. Subsequently, diffusion and convective coefficients iterate and converge until the best fit of simulated ion density profiles to the measured ones are obtained. The final D and v are plotted in Figs.
 | Fig. 10. The best-fit calculated ion density profiles of Mo29+, Mo30+ and Mo31+ during L-mode and H-mode phases associated with the experimental results. |
 | Fig. 11. Total molybdenum density obtained during L-mode and H-mode phases from the simulation results. |
Impurity radiation power density can be estimated according to PZ = ne nZ LZ, where LZ represents the line cooling rate.[27] In our case, central electron temperature is around 1.3 keV and 1.1 keV, and the central electron density are 3×1019 m–3 and 4.5×1019 m–3 during L-mode and H-mode, respectively. If we consider a molybdenum cooling factor of LMo ≈ 7× 10–32 W ⋅ m3, the radiated power density of molybdenum in the core region can be around 140 kW/m3 and 20 kW/m3 during H-mode and L-mode phases.[27]
The extreme ultraviolet spectrometer previously used on the EAST tokamak has been calibrated by comparing the calculated bremsstrahlung radiation intensity with the reading of CCD’s detector. The reconstructed emission profiles are obtained at the core plasma for Mo XXX, Mo XXXI and Mo XXXII. To facilitate next-step impurity transport studies, total molybdenum density profiles during L-mode and H-mode phases are obtained using the spectral lines and the STRAHL code. The results show that the molybdenum density is 3–4 orders of magnitude smaller than electron densities in typical EAST plasmas. Impurity accumulation happens during H-mode phase as a result of inward pinch in core plasma. Estimates of molybdenum radiated power density are 140 kW/m3 and 20 kW/m3 in core plasma during H-mode and L-mode phases. The present EUV spectrometer is designed to study the impurity behavior and impurity transport. By using the present method, the impurity accumulation behavior and the related transport mechanism will be studied in the future, which will be useful for exploring methods for relieving impurity accumulation.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |