† Corresponding author. E-mail:
Effects of oblique collisions of the dust acoustic (DA) waves in dusty plasma are studied by considering unmagnetized fully ionized plasma. The plasma consists of inertial warm negatively charged massive dusts, positively charged dusts, superthermal kappa distributed electrons, and isothermal ions. The extended Poincaré–Lighthill–Kuo (ePLK) method is employed for the drivation of two-sided Korteweg–de Vries (KdV) equations (KdVEs). The KdV soliton solutions are derived by using the hyperbolic secant method. The effects of superthermality index of electrons, temperature ratio of isothermal ion to electron, and the density ratio of isothermal ions to negatively charged massive dusts on nonlinear coefficients are investigated. The effects of oblique collision on amplitude, phase shift, and potential profile of right traveling solitons of DA waves are also studied. The study reveals that the new nonlinear wave structures are produced in the colliding region due to head-on collision of the two counter propagating DA waves. The nonlinearity is found to decrease with the increasing density ratio of ion to negative dust in the critical region. The phase shifts decrease (increase) with increasing the temperature ratio of ion to electron (κe). The hump (compressive, κe < κec) and dipshaped (rarefactive, κe > κec) solitons are produced depending on the angle (θ) of oblique collision between the two waves.
The charged dusts in plasma exist in space[1–5] (e.g. lower and upper mesosphere, cometary tails, planetary rings, planetary magnetospheres, inter-planetary spaces, interstellar media, etc.), laboratory experiment (e.g. Q-machine, plasma materials processing reactors[1]), etc. The wave dynamics, concerning the dust acoustic (DA) waves, dust ion acoustic (DIA) waves, dust acoustic rogue (DAR) waves, etc., facilitate the understanding of the electrostatic density perturbations and potential structures,[6–8]e.g., soliton, shock, rogue profile, vortices, etc., as observed in dusty plasma systems. The DA waves are produced[9] due to imbalance between the driving (provided by the inertia of the dust mass) and restoring forces (provided by the thermal pressure of ions and electrons). The linear and nonlinear structures of DA waves in unmagnetized weakly coupled dusty plasmas were investigated theoretically.[10–15]
Mamun et al.[16] have investigated the properties of DA solitary and shock waves with strongly coupled electrons and ions by taking into account the Boltzmann (vortex-like) distribution. The positive and negative charged dusts are also observed in space,[4,17–19] such as in upper mesosphere, cometary tails, Jupiter’s magneto-sphere, etc. The dust grains can be charged positively through three mechanisms:[20] photoemission due to ultraviolet photon flux, thermionic emission induced by radiative heating, and secondary electron emission from the surface of the dust grains. The existence of non-Maxwellian particles is observed from the satellite missions in astrophysical and space plasmas,[21–24] such as in the mercury, uranus, earth, and magnetosphere of Saturn. In these plasmas, the electrons’ distribution follows the power-law instead of Maxwellian distribution. On the other hand, the presence of nonthermal particles at high altitudes, e.g., solar wind and space plasmas, is found from the spacecraft observation.[25–29] Besides, the superthermal plasmas are observed in various experimental[30] plasmas, such as laser–matter interactions and plasma turbulence, and their properties are studied by considering the kappa distribution function.[31–33] Kappa distribution was first reported by Vasyliunas[31] to model the space plasmas and latter it was applied to different plasmas by several researchers.
Recently, several authors[34–37] have investigated DIA waves with kappa distributed electrons. Alinejad[37] has shown that the rarefactive DIA solitary waves and double layers may be produced, depending on the population of superthermal electrons. Ghosh et al.[38] have investigated the nonlinear properties of DIA solitary waves with small amplitude in dusty plasma comprised of electrons, ions, and dust grains, and found that the wave amplitude exponentially decreases with time due to the collisions of dust ions. Alinejad and Mamun[39] have studied the properties of obliquely propagating electrostatic waves in magnetized plasmas consisting of electrons, ions, and positrons, and noted that the basic features of solitary waves are modified significantly due to oblique collision, densities of superthermal electrons and positrons, and temperature ratio of electron to positron. The productions of solitons and their interactions among themselves are one of the most important nonlinear phenomena in dusty plasmas. Consequently, this has received special attention from plasma researches.
Ghorui et al.[40] have studied the characteristics of head-on collisions of counter propagating DIA solitary waves in magnetized quantum dusty plasmas by taking into account positively and negatively charged dust grains and found that the quantum diffraction parameter, ion cyclotron frequency, and density ratio of electron to ion play a significant role in modifying the phase shifts. The head-on collisions between the DA solitary waves have studied by Su and Mirie,[41] Jeffery and Kawahawa,[42] and Huang and Velarde[43] through employing extended Poincaré–Lighthill–Kuo (ePLK) method and found that the characteristic collective motion and collisional properties are affected by the dust charge variation. Xue[44] has also studied the effects of temperature ratio, density ratio of ion to electron, and dust charge variation on phase shifts due to collision of DA solitary waves and noted that the phase shifts are significantly modified by the dust charge variation. Li et al.[45] have investigated the interaction among Korteweg–de Vries (KdV) solitons in two-dimensional (2D) dusty plasmas. Besides, Han et al.[46] have studied the production of DA solitary waves and their interactions in weakly relativistic 2D thermal plasmas and determined the phase shifts and trajectories for an arbitrary angle of interactions. Chopra[47] has investigated the evolution of DAWs and characterized them in dusty plasmas. On the other hand, Boruah et al.[48] have studied the oblique collisional effects in strongly coupled dusty plasma and noted that dust acoustic solitons are formed at a certain collision angle. Das[49] has studied the propagation characteristics of the dust ion acoustic solitary waves in dusty plasma with Boltzmann electrons and found the streaming of dust for both compressive and rarefactive KdV solitons. Zahed et al.[50] have found in their study that the amplitude and width of the pseudo-potential have increased with increasing ion. Ferdousi et al.[51] have theoretically investigated the characteristic properties of obliquely propagating IASWs in the presence of ambient magnetic field in nonthermal plasma. They have observed that the characteristics of the solitary waves are significantly affected by the nonextensive electrons and positrons as well as external magnetic field. The collisional effects on instabilities of dust acoustic and dust ion acoustic waves were investigated[52] and it was also observed that the dispersion of the dust acoustic and dust ion acoustic waves are reduced due to the superthermal charge particles.
Owing to their importance and significance the oblique interaction phenomena and phase shifts in dusty plasmas are investigated. The plasma, considered here in this work, consists of inertial positively and negatively charged massive dusts, superthermal kappa distributed electrons and isothermal ions. The rest of this paper is organized as follows. In Section
Here, we consider the plasma that consists of inertial warm negatively charged massive dust with mass m1d and charge q1 = –Z1de, positively charged dust with mass m2d and charge q2 = +Z2de, superthermal kappa distributed electrons with mass me and charge –e, and isothermal positive ions with mass mi and charge +e, where Z1d (Z2d) is the charge number of negative (positive) dust. The charge neutrality condition can be defined as Z1dn1d0 + ne0 = Z2dn2d0 + ni0, where n1d0, ne0, n2d0, and ni0 are the equilibrium number density of warm negatively charged massive dust, kappa distributed electrons, positively charged dust, and isothermal ions, respectively. The normalized fluid equations of DA waves are considered as[53]







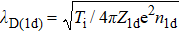

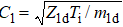




The two-sided Korteweg–de Vries (KdV) equations (KdVEs) are derived by employing ePLK perturbation method to investigate the oblique interaction phenomena of DA waves along with their phase shifts after oblique collision. Accordingly, the expansion of stretched coordinates and perturbed quantities can be considered[46] as














Solving expressions (









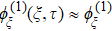
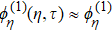

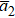
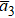
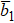
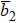
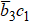
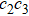
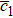
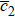
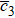
The next higher power of ε provides a set of PDEs and then after some algebraic manipulations and using Eqs. (

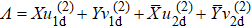
Integrating Eq. (







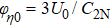
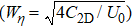

The un-magnetized dusty plasma consisting of inertial warm negatively charged massive dusts, positively charged dusts, superthermal kappa distributed electrons and isothermal ions as observed in space mentioned earlier, is considered to investigate the oblique interaction phenomena of DA waves. In this regard, the ePLK method is used to derive the two-sided KdVEs. The KdV-like soliton solutions presented in Eqs. (
The effect on nonlinear coefficient (C1N) with κe for Ti(e) is displayed in Fig.
It is mentioned earlier that the solitons Sξ and Sη travel toward the right and left direction, respectively. Therefore, one can see from Eq. (
Figures
Figures
Figures
The fully ionized un-magnetized dusty plasma is considered to investigate the oblique interaction phenomena of the DA waves. The plasma system consists of inertial warm negatively charged massive dusts, positively charged dusts, superthermal kappa distributed electrons, and isothermal ions. The KdVEs are derived by employing the ePLK method. The important results obtained in this paper are summed up as follows. New nonlinear wave structures are formed in the colliding region due to the head-on collision of the two counter propagating DA waves that depend on the degree of obliqueness. Near the critical value of ni(1d) (ni(1d) = 0.46), the nonlinearity decreases with ni(1d) increasing. The phase shifts decrease (increase) with Ti(e) (κe) increasing. The humpshaped (compressive) and dipshaped (rarefactive) solitons are produced depending on θ for κe < κec and κe > κec, respectively. The proposed model may be useful for explaining the results for both space (such as, lower and upper mesospheres, cometary tails, planetary rings, planetary magnetospheres, inter-planetary spaces, interstellar plasma media, etc.) and laboratory experiments (e.g., Q-machine plasma, RF plasma, microwave plasma, fusion plasma, etc.), where the inertial warm negatively charged massive dusts, positively charged dusts, superthermal kappa distributed electrons, and isothermal ions are the combined attribution.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] |










