† Corresponding author. E-mail:
We consider a self-assembled hybrid system, composed of a bilayer vesicle to which a number of colloids are adhered. Based on known results of membrane curvature elasticity, we predict that, for sufficiently deflated prolate vesicles, the colloids can self-assemble into a ring at a finite distance away from the vesicle equator, thus breaking the up–down symmetry in the system. Because the relative variation of the position of the colloidal ring along the vesicle endows the system with an effective elasticity, periodic cycles of inflation and deflation can lead to non-reciprocal shape changes of the vesicle–colloid hybrid, allowing it to swim in a low Reynolds number environment under reciprocal actuation. We design several actuation protocols that allow control over the swimming direction.
Vesicles are biomimetic, microscale containers, which can self-assemble from natural lipids,[1] as well as from synthetic polymers.[2] As such, they hold great promise as biocompatible carriers in drug delivery,[3,4] and as “cell mimics” in the context of bottom-up synthetic biology.[5,6] Moreover, simple vesicle-like containers are thought to be relevant in the context of the origins of life, as candidates for early protocells.[7,8]
Both in the drug delivery and in the cell mimicry contexts, it is of great interest to design vesicles that are able to actively swim, rather than passively diffuse. In the former case, active swimming would allow for enhanced and more targeted drug delivery. In the latter case, active swimming by vesicles would provide a minimal system with which phenomena such as e.g. collective motion in swimming microorganisms[9,10] could be probed.
However, in the absence of chemical reactions which may drive motion through phoretic mechanisms without any moving parts,[11–13] swimming at the microscopic scale requires nontrivial body deformations.[14] In particular, due to the absence of inertia and the consequent linearization of the field equations, microswimmers need to periodically deform their bodies in a way that is {non-reciprocal}: The shape deformations cannot remain unchanged under a time reversal. For a single swimmer, this means that the shape variation needs to describe a cycle in a two-dimensional or higher-dimensional shape space.[14–19]
In the context of vesicles, this implies that simple inflation and deflation cycles via external osmotic actuation cannot make a vesicle swim, even if the vesicle’s up–down symmetry is broken, as is the case for stomatocyte-shaped vesicles.[20] Evans et al.[21] showed that swimming by vesicles can be achieved only if the external actuation on the system is non-reciprocal, using two actuation parameters. In their proposed method, their actuation protocol describes a cycle in vesicle volume–membrane composition space, achieving a non-reciprocal shape deformation of the vesicle that leads to a net propulsion.
Non-reciprocal swimming strokes can also be achieved via reciprocal actuation, if the elasticity of the body is taken into the account.[17] For a slender filament clamped at one end, a reciprocal actuation of the other end can result in a propulsive thrust, when the filament is flexible.[22] In another example, a swimmer composed of two spheres joined together by an arm can in principle swim upon actuation of only one degree of freedom (the length of the arm), when the spheres exchange their unequal volume at the end of each stroke,[23] or when one of the spheres is elastic.[24,25]
Here, we design a self-assembled vesicle–colloid hybrid that can swim in response to reciprocal actuation of the vesicle volume, see Fig.
We consider a vesicle of spherical topology, with a bilayer membrane composed of a fixed number of lipids and thus a fixed surface area A. The membrane is described within the spontaneous curvature model,[20,29] and we focus on the case of a symmetric bilayer and identical solutions in the inner and outer compartments, so that the spontaneous curvature of the membrane is zero.
Under these conditions, the equilibrium (lowest bending energy) shape of the vesicle is governed by a single parameter, namely, its volume-to-area ratio[20]

The enclosed volume V, and therefore the volume-to-area ratio v, can be experimentally controlled by adjusting the concentration in the outer compartment of an osmotically-active solute, i.e., a solute to which the membrane is impermeable, such as salts and sugars.[29] If a vesicle has volume-to-area ratio v at a certain outer concentration cv of osmotically-active solute, increasing or decreasing this concentration to a new value cv′l ≠ cv will lead to deflation or inflation of the vesicle, respectively, towards a value v′ = (cv/cv′) v. Inflation and deflation of the vesicle can therefore be externally actuated by controlling the concentration of osmotically-active solutes in the system.
In Ref. [26], we investigated the adhesion of Janus colloids, with one strongly adhesive and one non-adhesive hemisphere, to non-spherical vesicles. We found that such colloids, when adhering to the outside of the vesicle, will be subject to curvature-induced forces that direct them towards regions of minimal mean curvature of the vesicle, in order to minimize the bending energy of the system. More precisely, the binding energy of the colloid was found to depend on the local mean curvature M of the membrane (when unperturbed by the colloid) as

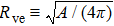
Typically, prolate vesicles have minimal mean curvature at their equatorial line. Thus, when adhering to such a prolate vesicle, a colloid will preferentially locate at the equatorial line. Moreover, the membrane-mediated interactions between two half-adhesive Janus colloids adhered on the outside of a vesicle have been shown to be repulsive.[30] Putting both contributions together, one would generally expect that when N ≥ 2 Janus colloids are put into contact with a prolate vesicle, they will self-assemble into a ring of equally-spaced particles around the vesicle equator (for the particular case of N = 2, this implies that the two particles will be located on opposite sides of the vesicle equator).
In fact, this is also what both experiments[31] and computer simulations[32] have found for partially-adhered uniform (non-Janus) colloids. However, as described in detail in Ref. [26], such uniform colloids are found in the partially engulfed state, which is sensitive to curvature-induced forces, only when the membrane–colloid adhesive strength is within a very narrow, finely-tuned range. Janus colloids, on the other hand, will always be in the curvature-sensitive partially engulfed state, as long as one side is non-adhesive and the other strongly adhesive, independently of the precise value of the adhesive strength. Therefore, we will focus here on Janus colloids as a more robust choice for the construction of vesicle–colloid hybrid swimmers.
We now look into the hydrodynamic interactions of the deforming vesicle and the adhered colloidal particles. These identical colloidal particles are uniformly distributed in a ring around the vesicle, and their motion is solely driven by the curvature-induced forces exerted by the membrane. As noted earlier, due to their microscopic sizes, the motion of the vesicle and the colloidal particles in the fluid is dominated by viscous dissipation. Thus, we may use the Stokes drag law to determine the instantaneous velocity of the vesicle as[33,34]




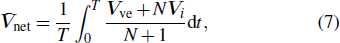
In Subsection
Indeed, for the lowest volume-to-area ratio v = 0.65 considered here, see the blue line in Fig.
We note that we have chosen v = 0.65 as the lower limit of the volume-to-area ratio because, at this value, a discontinuous transition from prolate shapes to oblate-discocyte shapes is expected to occur.[20] Nevertheless, because this transition is discontinuous, the prolate shapes will remain metastable for a wider range of values v < 0.65, and thus we expect that one could in practice deflate the vesicles even further. In fact, metastable prolates with volume-to-area ratios v < 0.65 have been observed both in experiment[35] and in computer simulations.[36]
The breaking of up–down symmetry in the location of the adhesive colloid ring for v ≲ 0.72 suggests that cycles of inflation and deflation between v = 0.65 and v = 0.71 could be used to induce directed swimming of the vesicle–colloid hybrid; see Fig.
However, this limitation is overcome if we allow for quick inflation or deflation. In this limit, the ring of colloids cannot adapt its location fast enough to the change in shape of the vesicle, and thus remains at a fixed location (as dictated by conservation of the membrane area above and below the ring during the shape change). Using this technique, we can design three different actuation protocols, leading to three different non-reciprocal swimming strokes:
Slow inflation, quick deflation: the ring of colloids approaches the equator quasistatically during slow inflation, remains there during quick deflation, and finally moves back towards its initial position along the deflated shape during a relaxation period; see Fig. Quick inflation, slow deflation: the ring of colloids remains far from the equator during quick inflation, moves towards the equator along the inflated shape during a relaxation period, and finally moves back quasistatically towards its initial position during slow deflation; see Fig. Quick inflation, quick deflation: the ring of colloids remains far from the equator during quick inflation, moves towards the equator along the inflated shape during a relaxation period, remains near the equator during quick deflation, and finally moves back towards its initial position along the deflated shape during a relaxation period; see Fig.
The possibility of designing non-reciprocal strokes in response to reciprocal actuation of a single degree of freedom (the volume v of the vesicle) arises due to the effective elasticity of the vesicle–colloid system, in a similar way as proposed for other low Reynolds number swimmers with a single degree of freedom, such as two-sphere swimmers with deformable spheres,[24,25] or flexible filaments.[22] In our case, the location of the colloid ring can “lag behind” the shape changes of the vesicle, leading to non-reciprocal swimming strokes in response to reciprocal actuation.
Note that the actuation protocols considered here make use of the limit cases of “very fast” inflation/deflation, in which the colloid ring does not have any time to respond to the shape changes, and “very slow” or quasistatic inflation/deflation, in which case the ring is at its equilibrium position at all times. The typical timescale for response of a colloid to shape changes can be estimated as follows: given overdamped dynamics 




Of course, at intermediate inflation and deflation speeds, there will be an interplay between the dynamics of colloid motion along the vesicle due to the curvature-induced forces, and the dynamics of vesicle shape changes due to the osmotic inflation and deflation. The limit-case protocols presented here serve as a proof of concept, and we expect that any moderately fast inflation and deflation protocol (so that the ‘slow’ quasistatic limit, shown in Fig.
The energy required for the cyclic motion of the vesicle–colloid system ultimately comes from the external changes in the concentration of osmotically active solute that cause inflation and deflation of the vesicle. If the vesicle initially has a volume V at a concentration cv of solute in the external compartment, and the external concentration is rapidly changed to a value cv′, the vesicle will experience an osmotic pressure difference ΔP = Pin – Pext = (cv – cv′) kBT. The work exerted by the osmotic pressure when the volume changes from the initial volume V to the final volume V′ = Vcv/cv′ is then given by 

Following the governing equations in Subsection 












In summary, we have proposed here a design for a vesicle–colloid hybrid that can swim at low Reynolds number, despite its reciprocal actuation. The vesicle–colloid hybrid will self-assemble under the right conditions: (i) the vesicle must be sufficiently deflated, so that its volume-to-area ratio is v ≲ 0.72; and (ii) the Janus colloids must have a side that strongly adheres to the membrane, and a side that does not. The actuation involves periodic changes in the volume of the vesicle, which can be induced via external control of the osmotic conditions in the system, e.g., the concentration of an osmotically active solute in the solution.
In this system, swimming in response to reciprocal actuation of the vesicle becomes possible thanks to two key innovations. First, we have found that for volume-to-area ratios of the vesicle below v ≲ 0.72, the line of lowest mean curvature of the vesicle (to which adhering colloids are spontaneously directed) moves away from the vesicle equator, thus allowing for the up–down symmetry of the vesicle shape to be spontaneously broken in the presence of the colloids. Second, the effective elasticity in the location of the colloid ring with respect to the vesicle results in non-reciprocal shape changes of the vesicle–colloid hybrid in response to reciprocal inflation–deflation cycles. We have proposed, as a proof of concept, three different actuation protocols that lead to swimming, but we expect non-reciprocal shape changes to be generic whenever inflation and deflation occur fast enough to avoid the quasistatic limit. We determined the swimming speed using a minimal model, and showed that the swimming directions in these protocols are remarkably different.
While the presence of the colloids allows for an easy route to non-reciprocal shape changes in response to reciprocal actuation, it is possible to think of other ways to achieve this goal even in a pure vesicle system, which could be explored in future work. One intriguing possibility would be to exploit the presence of hysteresis along the discontinuous discocyte-to-stomatocyte transition occurring at v ≈ 0.59 in the spontaneous curvature model,[20] in response to quasistatic (slow) changes in volume. Typically, one would expect the vesicle to remain in a metastable stomatocyte state as it is inflated beyond v > 0.59, and on the other hand to remain in a metastable discocyte state as it is deflated below v < 0.59. This process will thus automatically lead to a cyclic non-reciprocal shape change of the vesicle.
Lastly, we note that, while throughout the paper we have considered that inflation and deflation of the vesicle are externally actuated, strictly making the system externally driven rather than self-propelled, it is perfectly conceivable that the changes in volume could be programmed to be self-generated, e.g., by a catalytic reaction that produces or consumes osmotically-active solutes within the vesicle interior. Such a chemically-active vesicle would then constitute a fully autonomous microswimmer.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |




