† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51879022, 51979045, and 51906029), the Fundamental Research Funds for the Central Universities, China (Grant Nos. 3132019197, 3132020187, and 3132019037), the Projects for Dalian Youth Star of Science and Technology, China (Grant No. 2018RQ12), and the China Postdoctoral Science Foundation (Grant No. 2019M661084).
A free triangular jet (TJ1) and its counterpart initially passing a short circular chamber (TJ2) are numerically modeled using large eddy simulation (LES). This paper compares the near-field characteristics of the two jets in detail. To enable some necessary experimental validations, the LES conditions of TJ1 and TJ2 are taken to be identical to those measured by Xu et al. (Sci. China Phys. 56 1176 (2013)) and England et al. (Exp. Fluids. 48 69 (2010)), respectively. The LES predictions are found to agree well with those measurements. It is demonstrated that a strong swirl occurs near the chamber inlet plane for the TJ2 flow. At the center of the swirl, there is a cluster of three sink foci, where each focus is aligned midway between the original triangular apexes. In the vortex skeleton constructed from the time-averaged flow field, the vortices arising from the foci are helically twisted around the core of the jet. As the flow passes through the chamber, the foci merge to form a closed-loop “bifurcation line”, which separates the inward swirling flow and the outward oscillating jet. This global oscillation is regarded as a source node near the centerline of the chamber. If the chamber is removed for a “free” jet, i.e., TJ1, a cluster of three pairs of counter-rotating foci is produced and the net swirl circulation is zero, so the overall oscillation of the jet does not occur.
Turbulent jets play an important role in the fundamental research of jet flows and in industrial applications. Different from the traditional circular jets, noncircular jets, such as triangular jets, elliptical and rectangular jets, have advantages in entraining and mixing due to curvature difference of nozzle exits and instability produced by sharp corners.[1] Therefore, many researches have been conducted to clarify flow-field characteristics of noncircular turbulent jets over recent decades.[2–10] Significantly, Mi and Nathan[11] studied experimentally the centerline velocity characteristics of turbulent free jets issuing from nine different-shaped nozzles at a Reynolds number of 15000. The results showed that the jet from the isosceles triangular orifice produces the greatest decay rate in the near-field mean velocity of all the jets. Using a TSI 2-D laser Doppler velocimetry (LDV), Iyogun and Birouk[12] investigated the turbulent free jets issuing from five different nozzle geometries, i.e., triangular, smooth pipe, rectangular, contracted circular and square. They found that the triangular jet exhibits the highest rate of entrainment and spreading among the five nozzles. Note that the combustion process requires not only large-scale mixing to promote the bulk mixing of fuel and oxidizer, but also small-scale mixing to facilitate chemical reactions.[13] The turbulent characteristics of triangular jets provide superior advantages for its application in combustion systems. Therefore, in this work, turbulent jets issuing from sharped-edged triangular nozzle are studied in detail.
‘Axis-switching’, which is the change of the cross-sectional shape caused by the asymmetric distributions of pressure and mean flow field, is a distinguish phenomenon in noncircular jets.[14] In the case of triangular free jets, the key features of the axis-switching have been observed, e.g., by Gutmark and Grinstein,[15] Lindstrom and Amitay.[16] Lee[17] explained axis-switching in terms of self-induced motion of vortex lines in a shear layer of a triangular jet. In essence, the triangular-jet shear layer exhibits a cluster of six counter-rotating longitudinal vortices. At midway between the apexes, the vortex-induced velocity points away from the center of the jet. At the corners, it points toward the center of the jet. The jet flow therefore spreads more from the flat sides than from the corners of the exit, so the minor and major axes of the triangular jet would ‘switch’ places.[15]
The exit profile also plays an important role for the downstream development of the jet.[18] When a triangular jet passes through a short circular chamber, a partially confined triangular jet is formed and likely to oscillate with respect to the chamber axis under some conditions.[19] The confinement of the chamber causes the TJ2 to reattach the inside surface, and in the region upstream of the reattachment, a strong swirling flow exists adjacent to the triangular inlet. It was postulated in Ref. [17] that the shear-layer interaction between the swirl and the jet should produce three co-rotating longitudinal vortices, which then merge to form a single vortex within the chamber. As a result, the TJ2 may oscillate continuously.
To better understand the oscillation behavior, a more detailed flow field of TJ2 is needed to be visualized. This need however can be met only by direct numerical simulation (DNS) or large eddy simulation (LES). The instantaneous field measurements of velocity and vorticity are impossibly made experimentally inside the chamber. Xu et al.[19] performed LES for TJ2 flow and examined its mean and instantaneous characteristics. Yet, they did not investigate the presence of the chamber on the near-field characteristics of a triangular-jet flow, i.e., TJ2, against a “free” triangular jet TJ1. The present work by LES is designated to find the dynamic distinctions between TJ2 and TJ1 flows, which result from the presence of a circular chamber.
The rest of the paper is organized as follows. Section
In the LES modeling of the unsteady incompressible TJ1 and TJ2 flows, the following spatially filtered governing equations are solved with constant density and kinematic viscosity of the fluid:


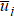
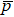
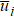
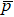
In Eq. (


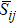


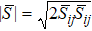
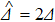
At the test-filter level, the stress tensor in Eq. (





For Eq. (
The present work utilizes a finite volume method available in Fluent 6.3, following the same simulation protocol given by Xu et al.[19] For example, the ‘SIMPLEC’ method is used for coupling the pressure and the velocity, the second-order three-level implicit scheme for the LES time step and the central difference scheme for a spatially discretized nozzle model.
For this simulation, both TJ1 and TJ2 nozzles have the same equivalent inlet diameter, i.e., De = 7.6 mm. The TJ2 chamber has a length of L = 8.75De and a diameter of D = 3.5De. The lip diameter at the exit plane of the chamber is d2 = 2.87De. The fully developed turbulent pipe flow is set as the jet inlet condition with a flow profile matching an empirical 1/7th power-law:[19,23]

The LES grid model for the TJ1 and TJ2 flow are shown in Figs. 
 | Fig. 1. Schematic diagram of (a) the TJ1 nozzle and (b) the TJ2 nozzle showing the geometric notations. Here D = 3.5De, L = 8.75De, d2 = 2.87De. |
 | Fig. 2. Computational grid of the TJ2 nozzle in (a) the longitudinal section (xy plane at z = 0) and (b) the cross-section (yz plane at x = D) of the chamber. |
To adequately simulate velocity gradients in the shear layer of the jet flow, it is necessary that the grid points are more densely spaced inside the chamber (for the TJ2) and adjacent to the corners of the triangle. The grid resolution Δ/De is 0.008 at the triangular inlet orifice. Moreover, the near-wall mesh is refined to capture the high shear in these regions. Calculation results show that y+ < 1 in the boundary layer meshes, where y+ is the dimensionless distance between the near-wall cell centroid and the boundary wall of the chamber and the inlet pipe, indicating the good performance of the present mesh. Finally, with 2 million grids for the present computational domain, the solution is sufficiently grid independent. This has been confirmed by initial checks, indicating that increasing the number of points by a factor of about 2 produces little change in the mean velocity field. To ensure that both the jet flows achieve a steady-state solution, the independence of time step has been tested.[19] For the present simulation, an optimized time step of ts = 50 μs is used to provide statistically independent samples (equivalent to 30000De/tsUe) for the purpose of time-averaging the flow fields. For TJ2, the duration of sampling provides 60 cycles of large-scale jet oscillation.
To validate the simulations by experiment, figure
 | Fig. 3. Centerline mean velocities of TJ1 and TJ2 obtained from LES predictions and PIV measurements. |
Manifestly, figure
It has been difficult to visualize the TJ2 flow experimentally and careful reconstruction of the flow has required data from a large assortment of flow visualizations and measurements.[29] Since a complete set of experimental data to disclose the TJ2 inside the chamber is impossible, the present LES data allows one to study in more detail the development of large-scale eddies in both the instantaneous and time-averaged flow fields. However, to acquire phase-averaged flow fields using LES presents a significant challenge due to highly aperiodic oscillation and characteristic low frequency of the TJ2.[23] In addition, there is a cost issue for a sufficiently long computational time that is necessary to attempt conditional averaging. The current LES approach therefore inevitably relies on visualizations of the instantaneous TJ1 and TJ2 to gain some understanding of their near flow field.
Figure
To visualize the shear layers of the TJ1 and TJ2 flows more clearly, the longitudinal cross sections (in the xy plane) of the three-dimensional streamline patterns in Fig.
 | Fig. 5. Central xy-plane fields of the instantaneous [(a), (b)] and time-averaged [(c), (d)] longitudinal velocities of TJ1 and TJ2 flows. |
For the TJ1 flow, the jet entrains ambient fluid in an axisymmetric manner and the spreading of the jet is accompanied by the decay in the streamwise velocity. As to the TJ2 flow, the reattachment phenomenon is accompanied by an asymmetric entrainment of the external ambient fluid and the eddies are larger than those of the TJ1 flow (see Figs.
Lee[17] suggested that a vortex structure inside a chamber plays a key role in maintaining the TJ2 oscillation. Therefore, it seems useful to begin this section with a description of the vorticity field obtained from the present LES results. Figures


 | Fig. 6. Instantaneous vorticity contours and streamlines in cross sections of TJ1 and TJ2 flows at different x/De. |
 | Fig. 7. Contours of the mean streamwise vorticity and streamlines in cross sections of the TJ1 and TJ2 flows at different x/De. |
 | Fig. 8. The positive Γ+/negative Γ− contributions and the total circulation (Γ = Γ+ + Γ−) in the time-averaged (a) TJ2 and (b) TJ1 flows. |
It is evident from Fig.
As indicated in Figs.
From the vorticity distributions and streamline patterns of the TJ1 and TJ2 flows, Section

Figure
 | Fig. 9. Iso-surface of the normalized second invariant of the velocity gradient tensor for instantaneous (a) TJ1 and (b) TJ2 flows at Q* = Q(Ue/De)2 = 1.0. |
The time-averaged distributions of Q*, where the dominant (coherent) structures of TJ1 and TJ2 are more distinguishable, are shown in Fig.
 | Fig. 10. Iso-surface of the normalized second invariant of the velocity gradient tensor for time-averaged (a) TJ1 and (b) TJ2 flows; Q* = 0.05, 0.02, 0.01. |
To summarize, the three co-rotating vortices which swirl towards the chamber wall are present only in the TJ2 flow. This seems to be the key difference between the TJ2 and TJ1 flows. Swirl must be present near the triangular orifice in order to destabilize the corner vortices, and if there is no swirl or the net circulation is zero in the near field, the jet oscillation will not be produced.
The present work has performed the LES simulations of a free triangular jet and its counterpart through a short cylindrical chamber at Reynolds number of Re = 17900. The simulations show significant differences between the flow characteristics of the two jets. Specifically, the presence of the chamber induces a strong swirling flow around the jet just downstream of the chamber inlet and enables the three pairs of innate longitudinal vortices to spiral in the shear layer between the swirl and the jet. As a result, the emerging jet from the chamber outlet oscillates “spontaneously” in a large-scale fashion. In the time-averaged flow of the oscillating triangular jet (TJ2), the vortices merge to form a closed-loop bifurcation line, which separates the swirling flow and the emerging jet. In the constructed vortex skeleton of the TJ2 flow, the longitudinal vortices spiral and reattach to the cylindrical wall before emerging out from the chamber. If the chamber is removed, the flow returns to a conventional free jet, where there is no net swirl circulation and no large-scale oscillation to ensue.
The innovation of this work is to enable a better understanding of the TJ2 oscillation by visualizing the three-dimensional detailed flow field inside the chamber instantaneously, which cannot be made by experiment.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |


