The reflection seismic survey is the most important method in the field of oil and gas reservoir exploration. The amplitude of seismic reflection wave carries the information about underground media. The reflection amplitude versus incident angle (AVA) can be used to predict hydrocarbon. The AVA from thin bed (including interbed) is one of the difficult points for reservoir prospection and prediction. The reflection from thin bed, calculated by Zeoppritz equation which is based on single phase elastic medium theory, was extensively studied.^[1–7] But the oil and gas reservoir is typical of porous media. The theory of wave propagation in porous media has been adopted in the field of soil, ocean sediment, and oil–gas reservoir, and so on.^[8–25] There are fast compressional wave (FP wave), slow compressional wave (SP wave) and conversed shear wave (CS wave) in porous media and the reflection at the interface of thick layer in porous media have been extensively studied.^[26–29] The fluid flows in pores will bring about wave attenuation and dispersion, and the wave dispersion in a seismic frequency range is proved in porous media.^[30,31] Frequency-dependent reflection amplitude versus incident angle (FDAVA) was developed in recent ten years.^[32–38] But there has been no paper to describe the frequency-dependent reflection from thin bed based on porous medium theory. In this paper, the Biot/Squirt model (BISQ) of porous medium is reviewed first. Then, the equations for calculating the frequency-dependent reflection coefficient from thin bed based on porous medium are obtained. The frequency-dependent reflection coefficients versus incident angle from thin sandstone reservoir and alternating thin bed of sandstone and mudstone are calculated and analyzed to answer the questions about the effect of wave dispersion, the thickness and structure of thin bed on wave reflection.

The BISQ equations of wave propagation can be expressed as follows:^[16]

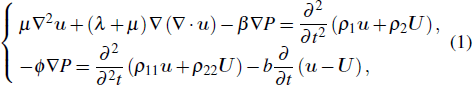
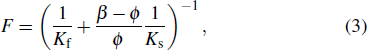
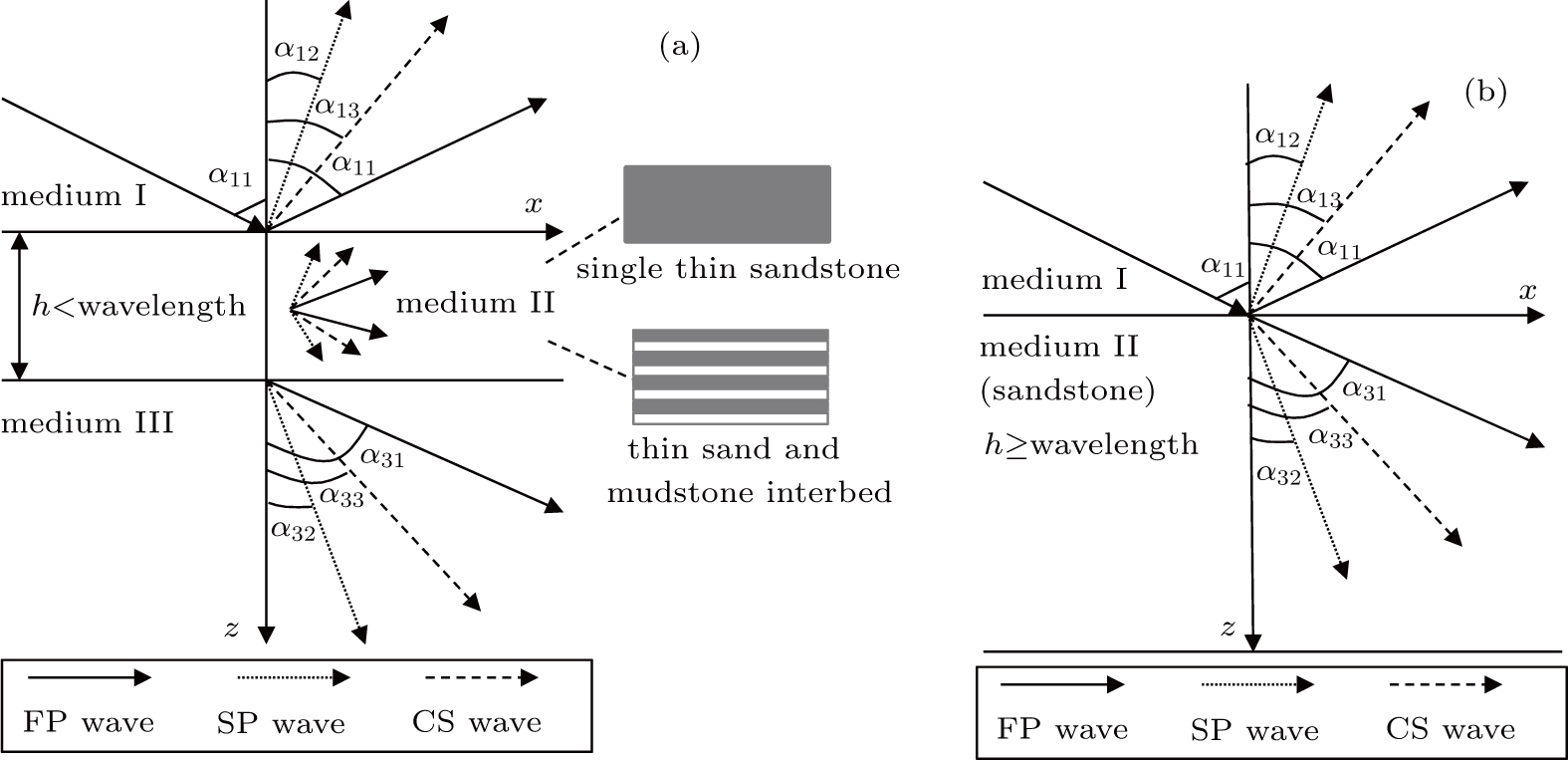
The geological thin reservoir model is shown in Fig. 1(a). The medium I is the covering mudstone and the medium III is the under mudstone. The medium II is the thin reservoir which is single thin sandstone or thin sandstone and mudstone interbed. The incident FP wave will introduce the reflected FP wave, SP wave, CS wave into medium I and transmitted FP wave, and the SP wave and CS wave into medium III. There are up-going and down-going FP wave, SP wave, and CS wave in medium II (Fig. 1). The frequency, velocity, attenuation, thickness, and structure of thin bed all affect the FDAVA response from thin reservoir. For better comparisons, figure 1(b) shows thick layer model.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Reflection and transmission from (a) thin bed and (b) thick layer based on BISQ theory.

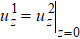
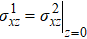
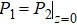
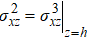
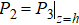
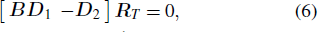
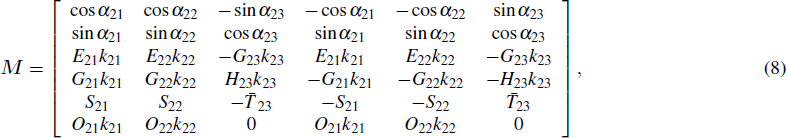
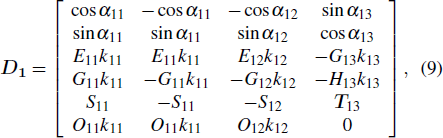
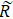
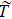
The boundary conditions of reflection and transmission can be expressed by , , , , , , , , , , , , u_x and u_z are the displacement components of solid. U_x and U_z the displacement components of fluid, σ_xx, σ_xz, and σ_zz the stress components, superscripts 1, 2, and 3 refer to medium I, medium II, and medium III, respectively, subscript x means the horizontal direction, z the vertical direction. P₁, P₂, and P₃ are the fluid pressures in medium I, medium II, and medium III, respectively, ϕ₁, ϕ₂, and ϕ₃ the porosities in medium I, medium II, and medium III, respectively, and h is the thickness of thin bed. Then, the FDAVA equations of a single thin bed in porous media can be obtained by

In the matter of thin interbed, the equation of AVA response can be expressed by Eq. (20). The definition of B_j is the same as that of B and is the number of the layers in the thin interbed.

The seismic common depth point gather (CDP) in time domain can be obtained from the following equation:

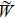
Because the wave number in those equations above is complex number and frequency dependent, so in the equations considered are the frequency-dependent velocity and attenuation. And the structure of thin interbed is considered in Eq. (20).

The parameters of mudstone (medium I and medium III) are set to be the same value (Table 1), which will introduce small velocity dispersion and low attenuation. The parameters of sandstone (medium II) are set to be the values (Table 1) which will introduce high velocity dispersion and high attenuation in a range of seismic frequency (Fig. 2). The thin interbed is made up of alternating superposition of sandstone (medium II) and mudstone (medium I). In Table 1, G_b is shear modulus of skeleton and K_b is the bulk modulus of skeleton.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Velocity and attenuation of FP wave versus frequency in sandstone.

Table 1.

Table 1.

Table 1. Parameters of model based on BISQ model. . Parameters ϕ/% η/Pa⋅s κ/mD ρf/(kg/m3) ρs/(kg/m3) Gb/GPa Kb/GPa Ks/GPa Kf/GPa r/mm Medium I 1 0.001 0.01 1000 2650 20 30 35 2.25 0.1 Medium II 30 0.03 1.25 900 2650 14.6 16 38 1.49 5

Table 1. Parameters of model based on BISQ model. .

We use biconjugate gradient-stabilized method to solve linear equations (Eq. (6) or Eq. (20)).^[39] The dispersion of FDAVA from 5-m-thin sandstone bed (Fig. 3(a)) is much higher and more complicated than that of thick layer (Fig. 3(b)). In the thick layer situation, the thickness of sandstone is much larger than the wavelength of seismic wave, and the reflection and transmission occur at the interface between mudstone and sandstone. The stack reflection amplitude of 0°–60° (which means adding the reflection coefficients with incident angle from 0° to 60°) from thick layer shows the property of low-frequency “bright spot” (Fig. 4(a)), but the stack reflection amplitude of 0°–60° of thin sandstone increases with frequency increasing (Fig. 4(b)). The difference between reflection coefficients of 10-Hz and 50-Hz waves from thin sandstone bed (Fig. 4(d)) is much higher than that from the thick layer (Fig. 4(c)). The CDP gather can be obtained by Eq. (21) and the wavelet is shown in Fig. 5. The low frequency component of CDP gather of thick layer (Fig. 6(a)) is much more obvious than that of the thin bed (Fig. 6(b)).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. FDAVA from (a) thick layer and (b) thin bed.

Fig. 4.

	Figure Option ViewDownloadNew Window
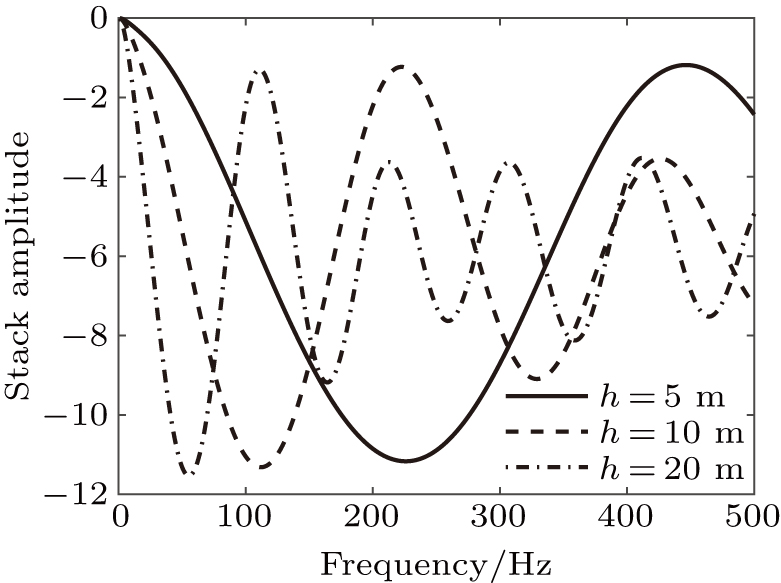
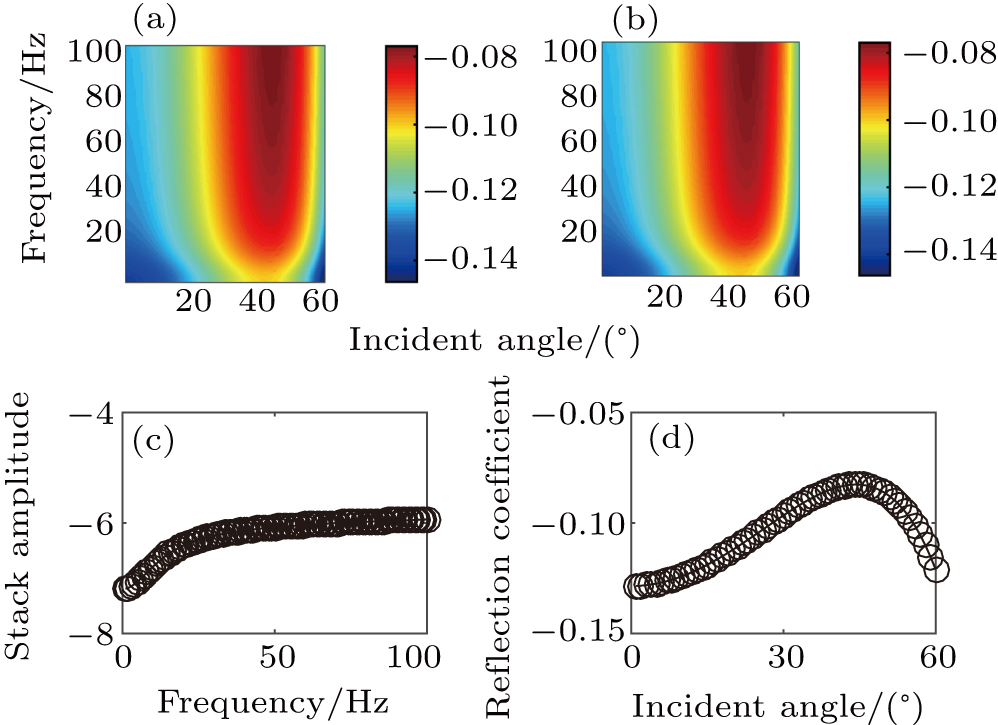
	Fig. 4. Stack reflection amplitude versus frequency for (a) thick layer and (b) thin bed, and reflection coefficient versus incident angle for (c) thick layer and (d) thin bed.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Seismic wavelet in (a) time domain and (b) frequency domain.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. CDP gathers of (a) thick layer and (b) thin sandstone bed.

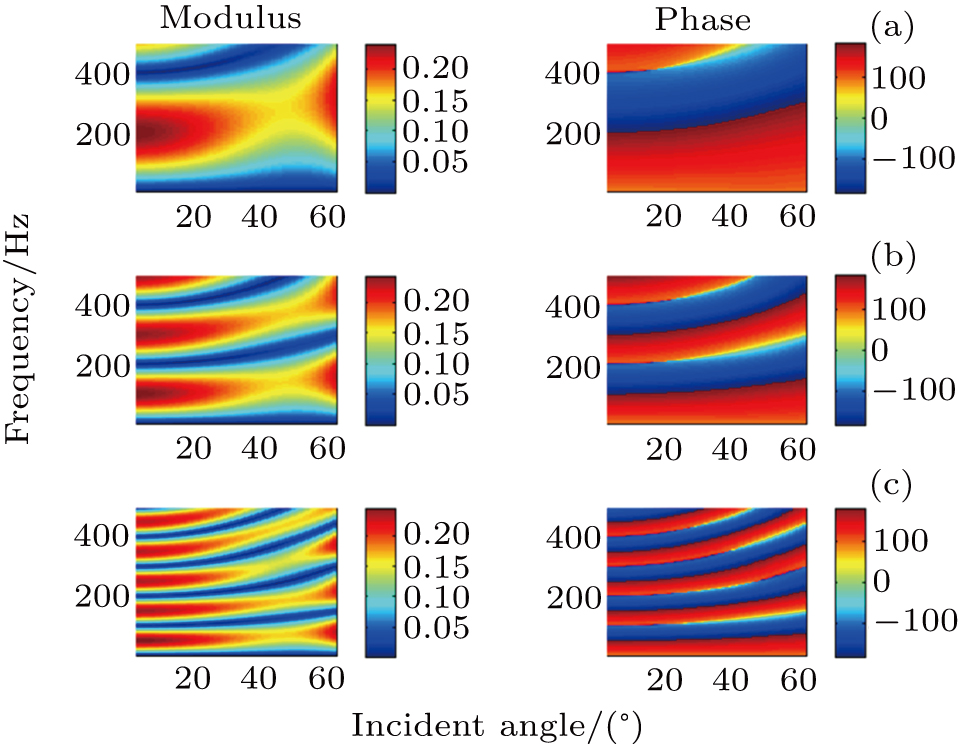
The modulus and phase of reflection coefficient show the periodic characteristic in frequency domain (Fig. 7). That is because equation (19) involves the periodic phase term. The periodic property has the relationship between the thickness of thin bed and incident angle. So, it has the potential application prospect to obtain the thickness of the thin bed. The amplitude envelope of frequency-dependent coefficients in frequency domain decays according to exponential function of e^{−2 himag(k₂₁ (ω))cos α₂₁} (Fig. 8).

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Periodic FDAVA from thin bed with h = 5 m (a), 10 m (b), and 20 m (c), separately.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Stack reflection amplitude of 0°–60° from thin bed with different thicknesses.

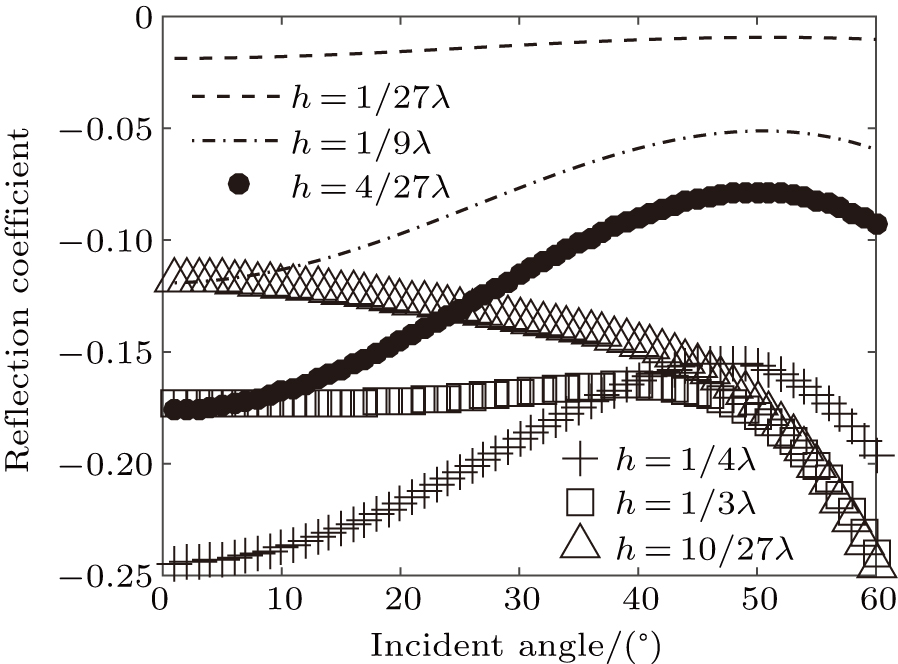
The reflection coefficient of 30-Hz wave increases with the thickness of thin bed increasing if the thickness is smaller than a quarter of wavelength. If the thickness is higher than a quarter of wavelength, the reflection coefficient decreases with thickness increasing when the incident angle is in a range of 0°∼ 40° (Fig. 9), and this incident angle range is important for seismic exploration.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Reflection of 30-Hz wave from thin bed with different thicknesses.

The general rules of FDAVA of thin interbed with fixed total thickness but different thicknesses of one layer () in the interbed are basically consistent with each other (Fig. 10). The number of layers in interbed can be obtained from . The stack reflection amplitude of 0°–60° (Fig. 11) and the reflection coefficient of 30 Hz (Fig. 12) wave increase slightly with the thickness of a layer in the interbed increasing.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. FDAVA from thin interbed (h = 7.5 m) with m (a), 0.5 m (b), and 1.5 m (c), separately.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Stack reflection amplitude of 0°–60° from thin interbed for h = 7.5 m.

Fig. 12.

	Figure Option ViewDownloadNew Window
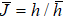
	Fig. 12. Reflection coefficient of 30-Hz wave from thin interbed versus incident angle for 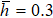m, 0.5 m, 1.5 m.

There is SP wave in the porous media. The SP wave is difficult to receive in the seismic exploration work. That is caused by the high attenuation of SP wave. We compare the FDAVA of two types of thick layers: in the first type, the SP wave in the boundary condition is considered but in the second type the SP wave in the boundary condition is not considered. They are almost the same (Fig. 13). The stack reflection amplitude and AVA of 30-Hz wave of 0.1-m thin bed with considering the SP wave in boundary condition are different from withthout considering the SP wave in boundary condition (Figs. 14(a) and 14(c)). But if the thickness of thin bed is 1 m, there is no obvious difference between them (Figs. 14(b) and 14(d)). That means the effect of SP wave on the AVA response cannot be ignored only if the thickness of thin bed is very small. So, in most conditions, the SP wave can be ignored in the boundary conditions.

Fig. 13.

	Figure Option ViewDownloadNew Window
	Fig. 13. FDAVA from thick layer with (a) and without (b) considering SP-wave, and (c) stack amplitude and (d) reflection coefficient of 30-Hz wave with (line) and without (circle) considering SP-wave.

Fig. 14.

	Figure Option ViewDownloadNew Window
	Fig. 14. Stack reflection amplitude from thin bed (h = 0.1 m (a) and 1 m (b)), and reflection coefficient of 30 Hz from thin bed (h = 0.1 m (c) and 1 m (d) with (broken line) and without (solid line) considering SP wave in boundary conditions.

The equations for calculating FDAVA from thin bed in porous media are obtained, with considering the effect of frequency-dependent velocity and attenuation, the thickness and structure of the thin bed. Through the numerical analysis, we obtain some conclusions below.

(i) The effect of SP wave on the FDAVA from thin bed in porous media can be ignored in most conditions except the fact that the thickness of thin bed is very small (cm level), which is likely to be caused by the high attenuation of SP wave, and the SP wave will decay in a short distance, which has been proved by the fact that it is difficult to detect slow P-wave in real survey.

(ii) The dispersion of FDAVA from the thin bed is much higher and more complicated than that from the thick layer, showing a periodic characteristic in frequency domain which is affected by the thickness of thin bed and incident angle. That is because the seismic wave dispersion of reservoir sandstone is much higher than that of surrounding mudstone. The envelope of stack reflection amplitude decays exponentially with frequency increasing, which is related to the thickness of thin bed, attenuation, and incident angle. So, it is possible to invert the thickness of thin layer by using the envelope of stack reflection amplitude changing with frequency. The stack reflection amplitude of FDAVA from the thick layer shows low frequency “bright spot”, but the stack reflection amplitude of FDAVA from the thin bed increases with frequency increasing. This phenomenon can be used for thin reservoir to be identified.

(iii) The reflection coefficient increases with the thickness of the thin bed increasing if the thickness is smaller than a quarter of wavelength and then decreases when the thickness is higher than a quarter of wavelength. The general rules of FDAVA obtained from thin interbeds whose total thickness is the same but each layer thickness may be changed, are basically consistent with each other. This is because in the example in this paper, although the thickness of the single layer in the thin interbed is different, the ratio between the sand and mudstone is the same because they are alternately distributed with the same thickness.