† Corresponding author. E-mail:
Project supported by the Science Fund from the Shaanxi Provincial Education Department, China (Grant No. 18JK0723).
Based on the generalized truncated second-order moments, an approximate analytical formula of the beam propagation factor M2 of high-power laser beams passing through the optical system with multiple hard-edged apertures is deduced. Numerical examples of the beams passing through an aperture-spatial filter are enclosed, and the influences of amplitude modulations (AMs) and phase fluctuations (PFs) on the beam propagation quality of high-power laser beams passing through the multi-apertured ABCD optical system are considered and discussed. It is shown that PFs are able to degrade the beam propagation quality of laser beams more than AMs when the high-power laser beams passing through the aperture-spatial filter, furthermore, one or two aperture-lens optical systems configured appropriate aperture parameters are both able to upgrade the beam propagation quality of high-power laser beams. The M2 factor of Gaussian beam passing through the multi-aperture optical system is a special case in this paper.
In the past decade, relying on the wide application from material processing and nonlinear optics to free-space optical communication and other fields, the high-power laser beams[1–4] have increasingly drawn attention, on the other hand, an increase in the laser output power inevitably results in the gain non-uniformity, gain saturation, nonlinear optical effects, and thermal effect further triggering beam distortions on both amplitude and phase which are able to impact the propagation properties of laser beams.[5–11] Therefore, it is practical important to study the propagation properties of laser beams with beam distortion, including amplitude modulations and phase fluctuations. In order to analyze propagation properties of laser beams with beam distortions theoretically, Manes and Simmons proposed statistical optics model of high-power laser beams for the first time.[12] Further studies[12,13] have shown that statistical optics methods can provide reliable estimates with experimental results and simulations. Besides, the beam propagation quality factor M2 introduced by Siegman[14] is a very useful beam parameter to feature propagation properties of laser beams in various applications.[15–18]
Generally, the larger the value of the factor is, the poorer the beam quality is. Meanwhile, the practical optical systems mostly are equipped with limited apertures which usually cause the laser beams propagating through these systems truncated. Thus, based on the mathematics model proposed by Manes and Simmons, a series of works concerning the propagation properties have been accomplished,[19–25] including M2 factor of truncated high-power laser beams passing through turbulent atmospheric and passing through optical system with an aperture. The results showed that the propagation properties of high-power laser beams are related to both amplitude modulations and phase fluctuations when passing through optical system with an aperture. In addition, it is also shown that when lasers propagate through turbulent atmosphere, the decrement of the turbulence effect on laser beams is caused by amplitude modulations and phase fluctuations. In 2004, by expanding the window function into complex Gaussian function sum, an approximate analytical recurrence formula specified for laser beams with amplitude modulations and phase fluctuations propagating through multi-apertured ABCD system was deduced by Lü et al.,[26] which provided a fast algorithm for simulating the beam propagation through complex optical trains with a series of apertures. This analytical expression is in satisfactory agreement with direct diffraction integration. To the best of our knowledge, as the valuable theoretical reference for the design and asses of high-power laser optical system, the generalized M2 factor of high-power laser beams passing through multi-apertured ABCD system has not been reported yet. With the truncated second-order moments method and expanding the hard-edged aperture function into a finite sum of complex Gaussian functions, in this paper, we deduce an approximate analytical expression for the generalized M2 factor of high-power laser beams passing through the multi-apertured ABCD optical system, and discuss the influence of beam distortions on M2 factor of laser beams. The approximate analytical propagation expression deduced in Ref. [26] is applied and the generalized M2 factor of high-power laser beams passing through an aperture-spatial filter system is calculated numerically in this paper.
In the space–time domain, the high-power laser beams with AMs and PFs introduced by Manes and Simmons[12] is featured with the mutual intensity J0 (


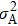
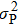


Letting


The high-power laser beams is assumed to propagate through the paraxial ABCD optical system consisting of m AiBiCiDi subsystems with m hard-edged apertures in the bi (i = 1, 2, …, m) width, as shown in Fig. 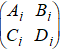
The window function of a rectangular aperture is expressed as T(x). According to Wen and Breazeale,[22] T(x) can be expanded into a finite sum of complex-valued Gaussian functions

The relevant parameters and expressions in this paper are subject to the corresponding parameters and expressions in Ref. [26]. On the basis of the mutual intensity expression Jm(x1, x2, z) at the output plane RPm in Ref. [26], the total power of high-power laser beams, passing through the m-th hard-edged rectangular aperture with width of bm at the m-th aperture plane z can be deduced as

The truncated second-order moments in the spatial domain of high-power laser beams through the m-th hard-edged rectangular aperture at the m-th aperture plane z is given by[28]

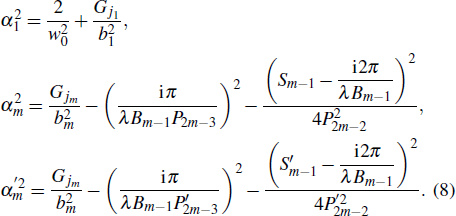


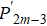





The corresponding cross second-order moment can be obtained as



Supposing that σ0 → ∞, 
In this section, some numerical calculations have been involved and accomplished with the above deduced analytical expression.
Figure 











The generalized M2 factor of high-power laser beams passing through the aperture-spatial filter system versus b2/w0 for different π0 and 






Figures 








Figure 
It is worth noting that further numerical calculations on the M2 factor of high-power laser beams passing through three or more aperture-lens optical system have as well been fulfilled. The results show that when the number of aperture-lens is equal to or larger than three, M2 factor with preset high-power laser beams parameters can be also minimized by optimal aperture parameters and the influence of AMs and PFs on the M2 factor is negligible with small width of the front apertures, the relevant detailed statements is omitted.
In this paper, the approximate propagation expression of beam propagation factor M2 of high-power laser beams passing through a multi-apertured optical ABCD system is derived with the truncated second-order moments method and by expanding the rectangular function into a finite sum of complex Gaussian functions, it can be applied to evaluate the beam propagation quality of high-power laser beams passing through a multi-apertured optical ABCD system. Numerical calculation results indicate the influence of the multi-apertures on the beam propagation quality of high-power laser beams. It is suggested that the M2 factor of high-power laser beams will be decreased with optimal beam parameters and aperture parameters regardless passing through one or two apertures, and the phase fluctuations have greater influence on M2 factor than amplitude modulations. The conclusions reported in this paper provides a reference for design and engineering applications of high-power laser spatial filter systems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |









