Cite this Article
Xu Jie-Feng, Yang Xiang-Bo, Chen Hao-Han, Lin Zhan-Hong. Extraordinary propagation characteristics of electromagnetic waves in one-dimensional anti-PT-symmetric ring optical waveguide network. Chinese Physics B, 2020, 29(6): 064201  
Permissions
Extraordinary propagation characteristics of electromagnetic waves in one-dimensional anti-PT-symmetric ring optical waveguide network
Xu Jie-Feng, Yang Xiang-Bo †, Chen Hao-Han, Lin Zhan-Hong
Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, School of Information and Optoelectronic Science and Engineering, South China Normal University, Guangzhou 510006, China

 

† Corresponding author. E-mail: xbyang@scnu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11674107, 61475049, 11775083, 61875057, 61774062, and 61771205), the Natural Science Foundation of Guangdong Province, China (Grant No. 2015A030313374), and the Special Funds for the Cultivation of Guangdong College Students’ Scientifific and Techonlogical Innovation, China (Grant No. pdjhb0139).

Abstract

In this paper, we design a one-dimensional anti-PT-symmetric ring optical waveguide network (1D APTSPROWN). Using the three-material network equation and the generalized Floquet–Bloch theorem, we investigate its photonic mode distribution, and observe weak extremum spontaneous anti-PT-symmetric breaking points (WBPs) and strong extremum spontaneous anti-PT-symmetric breaking points (SBPs). Then the transmission spectrum is obtained by using the three-material network equation and the generalized eigenfunction method. The 1D APTSPROWN is found to generate ultra-strong transmission near SBPs and ultra-weak transmission near WBPs and SBPs, with the maximal and minimal transmissions being 4.08× 1012 and 7.08× 10−52, respectively. The maximal transmission has the same order of magnitude as the best-reported result. It is not only because the distribution of photonic modes generated by the 1D APTSROWN results in the coupling resonance and anti-resonance, but also because the 1D APTSROWN composed of materials whose real parts of refractive indices are positive and negative has two kinds of phase effects, which results in the resonance and anti-resonance effects in the same kind of photonic modes. This demonstrates that the anti-PT-symmetric and PT-symmetric optical waveguide networks are quite different, which leads to a more in-depth understanding of anti-PT-symmetric and PT-symmetric structures. This work has the potential for paving a new approach to designing single photon emitters, optical amplifiers, and high-efficiency optical energy saver devices.

PACS: ;42.15.Eq;;42.25.Bs;;42.82.Et;
Keyword:;waveguides;;optical materials;;metamaterials;
1. Introduction

Controlling the propagation of the electromagnetic (EM) waves has been an important aspect of virtually every application that involves optical components. In 1998, by constructing a parity–time-symmetric (PT-symmetric) dynamic system, Bender et al.[1,2] found that there exist PT-symmetric breaking points in the system. In a PT-symmetric system, the Hamiltonian operator H, parity operator P, and time operator T still satisfy {H, PT} = 0. While the imaginary part of the potential function is beyond the value of PT-symmetric breaking points, the energy eigenvalues are complex numbers. In 2007, El-Ganainy et al.[3] first introduced the concept of parity–time (PT) symmetry into the optical system by founding a PT-symmetric optical system whose refractive index satisfies the condition: n(x) = n*( – x). Since then, several extraordinary optical properties[3–14] have been observed in PT-symmetric optical systems, such as power oscillations,[4–6] double refraction,[4] unidirectional invisibility,[7–10] absorption enhanced transmission,[11,12] coherent perfect absorbers and lasers[13,14] and so on. In Hermitian systems, these properties are not available.

In 2013, Ge et al.[15] designed an anti-PT-symmetric optical structure, whose refractive index satisfies the condition: n(x) = – n* ( – x), and the H, P, and T meet the condition: {H, PT} = 0. This artificial optical system has also aroused great interest[15–20] due to several extraordinary phenomena such as flat broadband light transport,[16] chiral mode conversion,[17] and ultra-strong transmission and reflection,[18] non-Hermitian particle-hole symmetry,[15,19] coherent switch.[20]

In 1998, optical waveguide networks[21–34] were proposed as a new kind of photonic bandgap (PBG) structure. Compared with photonic crystals, it exhibits excellent characteristics such as higher flexibility in structural symmetry,[21,23,24] and great convenience in measuring the phase and amplitude of EM waves.[21,23] Consequently, several interesting optical features and phenomena have been demonstrated in waveguide networks, such as extremely wide PBG,[24,25] comb-like optical transmission spectrum,[27,28] and ultra-strong photonic localization.[32,33]

So far, there has been no report that involves a combination of optical waveguide network and anti-PT symmetry. The PT-symmetric optical waveguide network is composed of materials whose imaginary parts of refractive indices are positive and negative simultaneously. Therefore, the gain and loss effects generated by the imaginary part of the refractive index exist in the network at the same time, and the gain and attenuation photonic modes cannot be distinguished.[33] However, the imaginary parts of the material refractive indexes are all either positive or negative in the anti-PT-symmetric optical waveguide network. It means that the anti-PT-symmetric optical waveguide network can only consist of gain or loss materials. In this paper, the anti-PT-symmetric optical waveguide network is composed of loss materials, whose imaginary parts of refractive indexes are all positive. EM waves propagating in the network will get a loss effect generated by the imaginary part of refractive index. In addition, the anti-PT-symmetric optical waveguide network is composed of materials with positive and negative real parts of refractive indices simultaneously. Therefore, when the EM wave propagates in the network, it will generate positive group velocity and negative group velocity, to enhance the flexibility and diversity of EM wave phase regulation, which are not available in PT-symmetric optical structure. By the phase regulation of the real part of the refractive index and the loss effect of the imaginary part of the refractive index, the anti-PT-symmetric optical waveguide network is likely to produce a deeper transmission valley than PT-symmetric optical waveguide network.

Therefore, in this paper, we design a one-dimensional anti-PT-symmetric ring optical waveguide network (1D APTSPROWN). We use the three-material network equation, the generalized eigenfunction method and the generalized Floquet–Bloch theorem to investigate the photonic mode distribution and transmission spectrum in the network. Unlike the PT-symmetric waveguide network reported previously,[33,34] exist in the 1D APTSPROWN are weak and strong extremum spontaneous anti-PT-symmetric breaking points (WBPs and SBPs) simultaneously. The 1D APTSPROWN can create not only ultra-strong transmission near SBPs, but also ultra-weak transmission near WBPs and SBPs, with the maximal and minimal transmissions being 4.08× 1012 and 7.08× 10−52, respectively. The maximal transmission has the same order of magnitude as the best results reported previously and the minimum transmission is about 40 orders of magnitude smaller than the PT-symmetric optical waveguide network with similar structures.[33] This is attributed to 1D APTSPROWN composed materials whose the real parts of refractive indices are positive and negative at the same time, so two kinds of phase effects co-exist. As a result, its photonic modes can not only interact with each other to generate coupling resonance and antiresonance, but also generate resonance and anti-resonance in the same kind of photonic mode. This indicates that the anti-PT-symmetric and PT-symmetric optical constructions are quite different. Our work may pave a new way for designing single photon emitter, optical amplifiers, high-efficiency optical energy saver devices, and other devices.

The rest of this paper is organized as follows. In Section 2, we introduce the theory and method. In Section 3 we present photonic mode analysis and extraordinary optical properties. We make mechanism analysis in Section 4. Finally, some conclusions are drawn in Section 5.

2. Theory and method
2.1. Network model: 1D APTSPROWN

As shown in Fig. 1, in this paper, we design a 1D APTSPROWN. At the entrance and exit, the vacuum waveguides of the length d1 whose refractive index is n0 = 1 are represented by the black lines. The green lines represent anti-PT-symmetric waveguides composed of three kinds of materials with refractive indexes n1, n2, and n3, respectively. Here,aij, bij – aij, and lij – bij represent the length of the first, second and third subwaveguide respectively and satisfy the condition: aij = bij – aij = lij – bij = lij / 3. In the network, adjacent nodes i and j are connected by two anti-PT-symmetric optical waveguides. d1 and d2 represent the lengths of the upper and lower arms of the waveguide, respectively. We set d1 : d2 = 1 : p, where p is a positive integer. Our work shows the result is best, when p = 2. Therefore, we only discuss the situation: p = 2.

Fig. 1. Structural diagram of 1D APTSPROWN, including one entrance, three unit cells, and one exit. EI, EO, and ER are the input, output, and reflected EM waves, respectively.

Since an anti-PT-symmetric optical structure can be realized by constructing a class of synthetic optical material whose refractive index satisfies n(x) = – n* ( – x),[15] n1, n2, and n3 are designed to satisfy the following relationship:

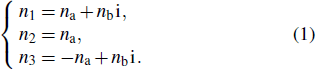
Studies have shown that in atomic vapor, the anti-PT symmetric medium can be experimentally realized.[19] In addition, anti-PT symmetry can also be realized in a dissipatively coupled optical system.[16] In this paper, we only discuss the anti-PT-symmetric optical waveguide network in principle, so we do not design it with specific materials. Firstly, we set na = 1.700. As for nb, it is a varying value and we need to combine the photonic pattern distribution in Subsection 3.1 to determine its value.

2.2. Three-material network equation

In 1D waveguide networks, linear combinations of two plane waves propagating in opposite directions can express the function of EM waves between nodes i and j below.

where the wave vector km = 2πvnm/c (m = 1, 2, 3).

The 1D APTSPROWN consists of three kinds of materials. For this kind of structure, by energy flux conservation, our group derived the three-material network equation in 2018 as follows:[33]

where

Using the three-material waveguide network equation, we can conveniently measure the phase and amplitude of EM wave in 1D APTSPROWN.

2.3. Generalized Floquet–Bloch theorem

For the structure like 1D APTSPROWN, we can use the dimensionless generalized Floquet–Bloch theorem,[23] whose expression is as follows:

where the nodal scale vector N, the Bloch wave vector of structure K, and the translation vector of the structure T are dimensionless. Compared with the Floquet–Bloch theorem, the dimensionless generalized Floquet–Bloch theorem can be used to study lattice waves with only topological translational periodicity like 1D APTSPROWN whose waveguide segments can be arbitrarily bent and folded. The generalized Floquet–Bloch theorem allows us to deduce the dispersion relation of 1D APTSPROWN, investigate its photonic mode distribution, and obtain extremum spontaneous anti-PT-symmetric breaking points (EBPs).

2.4. Generalized eigenfunction method

The transmission of EM waves can be calculated by the generalized eigenfunction method,[35] which converts wave transmission equations into transmission matrix, and considers the transmission coefficient and reflection coefficient as generalized wave functions.

3. Extraordinary optical properties
3.1. Distribution of photonic modes

The dispersion relations of 1D APTSPROWN can be obtained by the generalized Floquet–Bloch theorem and three-material network equation, whose expression is as follows:

In periodic optical waveguide networks, the Bloch wave vector K can reflect the change of the amplitude and phase of the EM wave. According to Eq. (5), when the EM wave propagates from the N-th unit cell to the (N + T)-th cell and K = a + bi, its amplitude will change a factor e−bT and the phase will change a factor ei aT. According to Eq. (6), if 1D optical waveguide network is composed of materials whose refractive indexes are all real, f(v) must be real. It is obvious that if |f(v)| < 1, K is a real number and b = 0, the amplitude of the EM wave in the network will not be changed, which is called ordinary propagation mode (OPM). Thus, only when |f(v)| > 1, does the structure Bloch wave vector K have a pair of complex conjugate solutions. In mathematics, when the imaginary part of K is negative and b < 0, the amplitude of the EM wave increases with factor e−bT increasing during the propagation in the network. We call it the gain propagation mode (GPM). On the contrary, because the imaginary part of K is positive and b > 0, the amplitude of the EM wave attenuates with a factor e−bT, which is called the attenuation propagation mode (APM). The GPM and APM both belong to non-propagation mode. But in physics, the optical waveguide network whose material refractive index is real, only presents an attenuation mechanism instead of gain mechanism. Therefore, it can only generate APMs for EM waves. It is obvious that |f(v)| = 1 is the demarcation between OPMs and non-propagation modes.

Unlike the optical waveguide network composed of materials whose refractive index is real, 1D APTSROWN is composed of complex refractive index materials. Thus, its Bloch wave vector K is always a pair of complex solutions with mutual conjugation, corresponding to APMs and GPMs in mathematics. In addition, the 1D APTSPROWN is composed of materials whose refractive indices' real parts are positive and negative simultaneously. Thus, in physics, in this kind of network there exist the attenuation and gain mechanisms at the same time. Consequently, the EM waves irrespective of the values of their frequencies propagate as APMs and GPMs at any position of the network, simultaneously. This demonstrates that we cannot simply determine the location of the anti-PT-symmetric breaking points simply through OPMs, APMs, and GPMs in the network.

Recently, our research group made an in-depth discussion on the properties of PT-symmetric optical waveguide network and defined the imaginary part of refractive index as the spontaneous PT-symmetric breaking point when.[33] Like the above case, K of the anti-PT-symmetric optical waveguide network possesses a pair of conjugate complex solutions. Therefore, we extend the previous research method of PT-symmetric optical waveguide network to the case of anti-PT-symmetric waveguide network.

When |f(v)| < 1, the imaginary part of K may be small and incapable of creating extraordinary transmission. In contrast, for |f(v)| > 1, the imaginary part of K can be large enough to create the extraordinary transmission. Consequently, when |f(v)| < 1, we define the GPM and APM generated by K as weak propagation modes (WPMs), and when |f(v)| > 1, we define the GPM and SPM generated by K as strong propagation modes (SPMs). The imaginary part of material refractive index nb is regarded as the spontaneous anti-PT-symmetric breaking point on the boundary of WPMs and SPMs.

As shown in Fig. 2, combining Eq. (6), we draw the distribution diagram of photonic modes of 1D APTSPROWN. The EBPs are located at the valley region of WPMs and SPMs, where |f(v)| = 1 and f(v) is continuous without derivative. Unlike the 1D PTSPROWN previously designed by our research group,[33] the 1D APTSPROWN has two kinds of EBPs (WBPs and SBPs). As shown in Fig. 2, WBPs and SBPs are located at the valley region of WPMs and SPMs, respectively. The first WBP and SBP produced by the network are called WBP-1 and SBP-1, respectively. When na = 1.700, the frequency of WBP-1 is 0.2941176471 c/d1 and the imaginary part of material refractive index nb is 4.21× 10−8. As for SBP-1, its frequency and the imaginary part of material refractive index nb are 0.5882352941 c/d1 and 3.24× 10−8, respectively. In order to compare the calculations with experimental results, we change the positions of the WBP-1 and SBP-1 by adjusting the length of the waveguide. When d1 = 456 nm or 912 nm, the WBP-1 and SBP-1 will be located near the communication wavelength λ = 1550 nm respectively.

Fig. 2. Distribution diagram of photonic modes, when na = 1.700. Here, yellow and blue regions represent SPMs and WPMs, respectively. (a) Overall picture, (b) enlarged drawing of WBP-1, and (c) enlarged drawing of the SBP-1.
3.2. Extraordinary optical properties

The ultra-strong and ultra-weak transmission can be obtained in 1D APTSPROWN near EBPs. Now, we take na = 1.700 for example to investigate the optical properties of 1D APTSPROWN. (i) In Subsection 3.1, the calculated value of nb is 3.24× 10−8 at the SBP-1. As shown in Fig. 4, at SBP-1, the network can generate the ultra-strong and ultra-weak transmission, where the maximal and minimal transmission are 4.08× 1012 and 1.12× 10−16, respectively. The maximal transmission is of the same order of magnitude as the best results reported previously.[33] (ii) The value of nb calculated in Subsection 3.1 is 4.21× 10−8 at the WBP-1. Compared with SBP-1, the network can only generate ultra-weak transmission at WBP-1, where the minimal transmission is 1.92× 10−33 which is nearly 17 orders of magnitude better than the result of SBP-1. (iii) No matter whether the network is at SBPs or the WBPs, when the value of nb increases appropriately, the amplitude of the ultra-strong transmission peak will decrease, but the depth of the ultra-weak trough will increase significantly. As shown in Fig. 3(a), when the imaginary part of the refractive index nb increases from 4.21× 10−8 to 8× 10−6 near the WBP-1, the minimum value of transmission will change from 1.92× 10−33 to 7.08× 10−52, which is about 40 orders of magnitude deeper than PT-symmetric optical waveguide network with similar structures.[33] Whereas, as shown in Figs. 3 and 4, it can be observed that if the imaginary part of the refractive index nb is too large, neither ultra-strong nor ultra-weak transmission exists (red lines). In addition, if we reduce the value of nb, the height of the ultra-strong transmission peak and the depth of the ultra-weak trough will decrease significantly.

Fig. 3. Transmission spectrum of 1D APTSPROWN corresponding to different values of nb near WBP-1 when na = 1.700. Blue, purple, black, and red lines represent the results that the values of nb are 8× 10−6, 4.21× 10−8, 4.21× 10−10, and 4.21× 10−2, respectively. (a) Overall spectrum and (b) zoomed part of spectrum.
Fig. 4. Transmission spectrum of 1D APTSPROWN corresponding to different values of nb near SBP-1 when na = 1.700. Blue, purple, black, and red lines represent results that values of nb are 3.24× 10−7, 3.24× 10−8, 3.24× 10−9, and 3.24× 10−3, respectively. (a) Overall spectrum and (b) zoomed part of spectrum.
4. Mechanism analysis

The 1D APTSPROWN can produce extraordinary ultra-strong and ultra-weak transmissions due to special phase effect and photonic mode. (i) When the EM wave propagates in the material whose real part of refractive index is positive, the phase of the wave function increases with propagation distance increasing. However, in the material whose real part of refractive index is negative, the phase of the wave function decreases with propagation distance increasing. Thus, the EM waves have two kind of phase effects propagating in 1D APTSPROWN composed of materials whose real parts of refractive indices are positive and negative at the same time. The material with a negative real part of refractive index is called the left-handed material. Unlike the material with a positive real part of refractive index, the transmitted wave and the incident wave are on the same side of the normal line as the EM wave propagating in this material. This means that there is not only one propagation direction of EM waves in the anti-PT symmetric optical waveguide network. However, the PT symmetric optical structure is composed of materials only with a positive real part of refractive index, so the above properties do not exist in the PT symmetric optical structure. The EBPs appear on the boundary of WPMs and the SPMs, where f(v) is continuous without derivative and |f(v)| = 1. Because of two kinds of phase effects of 1D APTSPROWN, WPMs and SPMs can generate resonance and antiresonance, respectively. When the phases of EM waves of the same kind of propagation modes (WPMs or SPMs) differ by (2n + 1)π (n is an integer.) and meet each other, EM waves will generate anti-resonance, forming a transmission valley. If they differ by 2nπ and meet each other, EM waves will resonate to form a transmission peak. This is the first kind of gain and attenuation mechanism generated by 1D APTSPROWN. (ii) When the EM waves propagate in the material with positive imaginary part of refractive index and the imaginary part of wave vector is k (k > 0), the amplitude of the wave function changes by a factor of ekx. The attenuation effect of EM wave increases with the value of nb increasing. In the 1D APTSPROWN, the imaginary parts of the refractive index of the first and third subwaveguide are both positive. However, as shown in Fig. 2, the imaginary parts of the refractive index of WBP-1 and SBP-1 are very small (only 10−8). This indicates that the loss effect generated by the imaginary part of the material only has a secondary influence on the 1D APTSPROWN producing ultra-strong and ultra-weak transmission. In Subsection 3.1, we divided the photonic modes of the network into the WPMs and SPMs. At the EBPs, the WPMs and SPMs can generate coupling resonance and antiresonance, respectively. This is the second kind of gain and attenuation mechanism generated by the 1D APTSPROWN.

4.1. Real part of the refractive index

The value of the real part of refractive index na can significantly affect the degree of phase variation of EM wave in the 1D APTSPROWN, which can change the positions of the EBP. The values of nb selected in Table 1 are very small (only 10−8) and close to each other. Therefore, we can approximately think that the imaginary parts of refractive indices have the same effect in 1D APTSPROWN.

Table 1.

Data of 1D APTSPROWN optical waveguide network at SBP-1 when value of na changes.

.

The properties of ultra-weak transmissions produced by the network are similar for WBPs and SBPs, with only a numerical difference. In order to avoid duplication of work, we only discuss the latter. As shown in Table 1, when the value of na changes, the 1D APTSPROWN presents the following properties: (i) No matter whether the value of na increases or decreases, the position of the EBP will change, and the real part of refractive index na and the frequency v have an obvious negative correlation in numerical value. (ii) Nomatter whether the value of na increases or decreases, both ultra-strong and ultra-weak transmission produced by the network are of the same order of magnitude at SBP-1. In general, the value of na can significantly affect the location of the EBP, but no matter where the EBP is, it still located on the boundary of WPMs and SPMs. Because the two kinds of photonic modes (WPMs and SPMs) can interact with each other to generate resonance and antiresonance, the network can produce ultra-strong transmissions at SBPs, ultra-weak transmissions at SBPs and WBPs.

4.2. Imaginary part of refractive index

The value of the imaginary part of nb not only is related to the loss effect of 1D APTSPROWN, but also can make the network deviate from EBPs. For the network of anti-PT symmetric waveguide, the resonance and antiresonance effect caused by the real part of the refractive index are the most intense at EBPs. As shown in Fig. 5, increasing or decreasing the value of nb will cause the network to be far away from EBPs, leading the resonance or anti-resonance capacity of the network to decrease. The minimum transmission is related not only to the anti-resonance effect of the network, but also to the loss effect of the imaginary part of the refractive index. Thus, when the combined effect of the anti-resonance effect and the material loss effect is strongest, the minimum transmission can be generated. If we appropriately increase the value of nb, although the anti-resonance effect of the network is weakened, the transmission valley can still deepens. However, when we increase the value of nb too much, although the loss effect of the material is enhanced, the anti-resonance effect of the network is very weak due to the great deviation of network from EBPs, and no transmission valley is generated. According to Subsection 3.1, nb value of the WBP-1 and the SBP-1 are 4.21× 10−8 and 3.24× 10−8, respectively. The 1D APTSROWN composed of materials whose refractive indices are positive and negative has two different phase effects, so WPMs and SPMs can generate resonance and anti-resonance respectively near EBPs. Combining Figs. 3 and 4, when the value of nb changes and na = 1.700, the 1D APTSPROWN has the following properties: (i) as shown by the upward arrow in Fig. 5, if the value of nb of the WBP-1 and the SBP-1 increase to 8× 10−6 and 3.24× 10−6, respectively, the network will only have WPMs near WBP-1 and SPMs near SBP-1. The loss effect of network is enhanced because the value of nb increases. Simultaneously, near the WBP-1, the WPMs generate the anti-resonance effect and the minimum value of transmission produced by 1D APTSROWN is 7.08× 10−52, which is nearly 19 orders of magnitude better than that of the transmission generated at WBP-1. As for the SBP-1, the SPMs generate the resonance effect and the anti-resonance effect, and the network can still produce ultra-strong transmission and ultra-weak transmission. Its maximal transmission is nearly 2 orders of magnitude lower than that of SBP-1, but its minimal transmission is nearly 2 orders of magnitude better than that of SBP-1. In addition, as shown by the red lines in Figs. 3 and 4, if the value of nb is too large, the network will be far away from the EBPs, and the network cannot produce extraordinary optical properties. (ii) As the downward arrow shows in Fig. 5, if the value of nb of the WBP-1 and the SBP-1 decrease to 4.21× 10−10 and 3.24× 10−10, respectively, the network will only have WPMs near WBP-1, and SPMs near SBP-1. The loss effect of network decline as the value of nb decreases. Simultaneously, near the WBP-1, the SPM generates the anti-resonance effect but the minimum value of transmission is larger than that of WBP-1. As for the SBP-1, the SPMs can generate resonance and anti-resonance effect and the network can still produce the ultra-strong and ultra-weak transmission. However, the height of the ultra-strong transmission peak and the depth of the ultra-weak trough will decrease significantly.

Fig. 5. Photonic distribution of 1D APTSPROWN at SBPs and WBPs, when the value of nb changes. Upward and downward arrow indicate that nb value increases or decreases. (a) Result of WBP and (b) result of SBP.
5. Conclusions

In this paper, we first introduce the concept of anti-parity–time symmetry into the optical system by constructing 1D APTSPROWN. Using the three-material waveguide network equation, the generalized Bloch theorem, and the generalized eigenfunction method, we investigate two kinds of photonic mode distributions (WPMs and SPMs) and transmission spectrums. At SBPs, 1D APTSPROWN can produce ultra-strong and ultra-weak transmission, where the maximal transmission is 4.08× 1012. The maximal transmission is of the same order of magnitude as the best results reported previously. Compared with SBPs, the network can only generate ultra-weak transmission near WBPs, where the minimal transmission is 7.08× 10−52 which is nearly more than 36 orders of magnitude better than the result of SBPs. It is because WPMs and SPMs generate coupling resonance and antiresonance at EBPs. Additionally, the 1D APTSPROWN composed of materials whose refractive indices are positive and negative has two kinds of phase effects, resulting in resonance and antiresonance effect of WPM and SPM respectively. This complex coupling effect causes the network to produce ultra-strong and ultra-weak transmission. Our work may pave a new way for designing single photon emitter, optical amplifiers, high-efficiency optical energy saver devices, and other devices.

Reference
[1] Bender C M Boettcher S 1998 Phys. Rev. Lett. 80 5243
[2] Bender C M Boettcher S Meisinger P N 1999 J. Math. Phys. 40 2201
[3] El-Ganainy R Makris K G Christodoulides D N Musslimani Z H 2007 Opt. Lett. 32 2632
[4] Makris K G El-Ganainy R Christodoulides D N Musslimani Z H 2008 Phys. Rev. Lett. 100 103904
[5] Rüter C E Makris K G El-Ganainy R Christodoulides D N Segev M Kip D 2010 Nat. Phys. 6 192
[6] Zheng M C Christodoulides D N Fleischmann R Kottos T 2010 Phys. Rev. 82 010103
[7] Lin Z Ramezani H Eichelkraut T Kottos T Cao H Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
[8] Regensburger A Bersch C Miri M A Onishchukov G Christodoulides D N Peschel U 2012 Nature 488 167
[9] Zhu X Feng L Zhang P Yin X Zhang X 2013 Opt. Lett. 38 2821
[10] Feng L Zhu X Yang S Zhu H Zhang P Yin X Wang Y Zhang X 2014 Opt. Express 22 1760
[11] Guo A Salamo G J Duchesne D Morandotti R Volatier-Ravat M Aimez V Siviloglou G A Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
[12] Zhang Z Miao P Sun J Longhi S Litchinitser N M Feng L 2018 ACS Photon. 5 3016
[13] Longhi S 2010 Phys. Rev. 82 031801
[14] Chong Y D Ge L Stone A D 2011 Phys. Rev. Lett. 106 093902
[15] Ge L Tuereci H E 2013 Phys. Rev. 88 053810
[16] Yang F Liu Y You L 2017 Phys. Rev. 96 053845
[17] Zhang X Jiang T Chan C T 2019 Light-Sci. Appl. 8 88
[18] Wang H Kong W Zhang P Li Z Zhong D 2019 Appl. Sci.-Basel 9 2738
[19] Peng P Cao W Shen C Qu W Wen J Jiang L Xiao Y 2016 Nat. Phys. 12 1139
[20] Konotop V V Zezyulin D A 2018 Phys. Rev. Lett. 120 123902
[21] Zhang Z Q Wong C C Fung K K Ho Y L Chan W L Kan S C Chan T L Cheung N 1998 Phys. Rev. Lett. 81 5540
[22] Dobrzynski L Akjouj A Djafari-Rouhani B Vasseur J O Zemmouri J 1998 Phys. Rev. 57 R9388
[23] Wang Z Y Yang X 2007 Phys. Rev. 76 235104
[24] Cheung S K Chan T L Zhang Z Q Chan C T 2004 Phys. Rev. 70 125104
[25] Lu J Yang X Zhang G Cai L 2011 Phys. Lett. 375 3904
[26] Li M H Liu Y Y Zhang Z Q 2000 Phys. Rev. 61 16193
[27] Yang X Song H Liu T C 2013 Phys. Lett. 377 3048
[28] Wang Y Yang X Lu J Zhang G Liu C T 2014 Phys. Lett. 378 1200
[29] Vasseur J O Djafari-Rouhani B Dobrzynski L Akjouj A Zemmouri J 1999 Phys. Rev. 59 13446
[30] Mir A Akjouj A Vasseur J O Djafari-Rouhani B Fettouhi N El E H Dobrzynski L Zemmouri J 2003 J. Phys.: Condens. Matter 15 1593
[31] Stoytchev M Genack A Z 1997 Phys. Rev. 55 R8617
[32] Feng L Xu Y L Fegadolli W S Lu M H Oliveira J E B Almeida V R Chen Y F 2013 Nat. Matter. 12 108
[33] Zhi Y Yang X Wu J Du S Cao P Deng D Liu C T 2018 Photon. Res. 6 579
[34] Wu J Yang X 2017 Opt. Express 25 27724
[35] Liu Y Hou Z Hui P M Sritrakool W 1999 Phys. Rev. 60 13444