Cite this Article
Ma Dongfang, Han Yueyi, Jin Sheng. Solid angle car following model. Chinese Physics B, 2020, 29(6): 060504  
Permissions
Solid angle car following model
Ma Dongfang1, Han Yueyi1, Jin Sheng2, †
Institute of Marine Sensing and Networking, Zhejiang University, Zhoushan 316021, China
Institute of Intelligent Transportation Systems, Zhejiang University, Hangzhou 310058, China

 

† Corresponding author. E-mail: jinsheng@zju.edu.cn

Project supported by the National Key R&D Program of China (Grant No. 2018YFB1601000).

Abstract

Existing traffic flow models give little consideration on vehicle sizes. We introduce the solid angle into car-following theory, taking the driver’s perception of the leading vehicle’s size into account. The solid angle and its change rate are applied as inputs to the novel model. A nonlinear stability analysis is performed to analyze the asymmetry of the model and the size effect of the leading vehicle, and the modified Korteweg–de Vries equation is derived. The solid angle model can explain complex traffic characteristics and provide an important basis for modeling nonlinear traffic phenomena.

PACS: ;05.60.-k;;05.70.Fh;;11.90.+t;
Keyword:;solid angle;;car following;;nonlinear stability;;vehicle size;;asymmetry;
1. Introduction

Nowadays, the traffic congestion problems our society is facing have been the focus undeniably today, influencing people’s daily life and schedule. In order to solve these problems, many scholars focus on the traffic flow theory which is a kind of core theory for traffic management. The definition of traffic flow is a system used to describe the interacting vehicles of which the feature is self-driven and many-particle.[1] Car-following theory, which can explain the complex phenomena of traffic flow such as critical phase transitions,[2–15] is indispensable in microscopic traffic modeling.

The theory of car following has been developed for a long time. Since 1950, numerous researchers have come up with different forms of car-following models successively. From the perspective of statistical physics, vehicles are considered as self-driven interacting particles. The physicists build microscopic car following models by introducing some essential factors which can describe the basic properties of the actual traffic flow.

A classic idea has been widely accepted that the car-following behavior is a complex process which can be regarded as a response to a stimulus. As a result, many researchers have proposed different kinds of car-following models based on the above idea of stimulus-response framework. Of all car-following models, the kind of models concerning with optimal velocity is very classical in which the acceleration is expressed as a response to the stimulus containing different kinds of factors. The models listed below are more representative.

Bando[2] proposed an optimal velocity (OV) model in the 1990s to solve the problem of the excessive acceleration in Newell model

where an(t) is the accelerate of the n-th car at time t; α is the sensitivity coefficient, the reciprocal of response time; U[Δ sn(t)] is the function of optimal velocity which derive the velocity excepted by drivers according to the headway; Δ sn(t) is the headway between the n-th car and its leading car at time t; un(t) means the velocity of the n-th car at time t.

The parameters of the OV model were calibrated by Helbing and Tilch.[20] In addition, they pointed out the existing problems and proposed a generalized force (GF) model

where λ is the sensitivity coefficient of relative velocity; Δ un(t) is the relative velocity between the n-th car and the leading car at time t. The first term represents the acceleration of the car while accelerating and the second term represents the acceleration caused by the interaction between two cars.

Considering the effect of positive speed difference, Jiang et al.[21] came up with a more comprehensive model called full velocity difference (FVD) model

This model can describe the process of starting vehicles better than other models. Many scholars investigated the nonlinear features of traffic flow by extending the FVD model. The new model proposed in this paper puts the solid angle as the new factor based on the FVD model.

Recently, lots of researchers proposed extended car-following models based on the former research results, which is of great significance for development of car-following theory. Sun et al.[22] proposed an extended car-following model by considering drivers memory and average speed of preceding vehicles with control strategy, they used different methods to analyze the model. Wang et al.[23] came up with a novel two-lane lattice hydrodynamic model considering lane changing behavior and passing behavior on curved roads. It is a breakthrough in traditional car following models. Besides, they[24] considered the influence of other factors, the empirical lane changing rate and the self-stabilization effect, and put forward an extended lattice hydrodynamic model.

Nevertheless, car following is a behavior that is highly constrained in the driver’s decision. Apparently, the drivers are unable to estimate the distance and velocity exactly. They usually use their sensory ability to judge the behavior of the leading car and respond accordingly. Considering the realistic situation, Jin et al.[18] proposed a new model using the visual angle information as stimulus from the perspective of statistical physics based on the stimulus-response framework. The expression is as follow:

where θn(t) is the visual angle formed by the width of the leading car and the distance between the two cars. This model takes better account of human drivers’ characteristics but there are still shortcomings.

In the past research, it is assumed crucially in the current car-following model that all of vehicles are modeled as particles, and the type and size of vehicles are neglected. Nevertheless, the drivers of the following vehicles will be influenced enormously by the size of the leading vehicles. In addition to relative velocity and distance with proceeding vehicle, it can be found that the leading vehicle types could have a great impact on the car following behavior. Due to the larger size and the worse braking capacity of trucks, the headway is larger when a driver follows a truck rather than a car,[16] so we can conclude from the above phenomena that the driving behavior is impacted by the type of leading vehicle.[17] Thus, it is significant to model the effects of vehicle size on car following behavior. To our knowledge, the effects of vehicle size on the car-following behavior have not been taken into consideration in most of the models.[18] We consider that it is of importance to put forward a solid angle model with considering the effect of vehicle size and to explore the characteristics of the novel model.

In this paper, we propose a dynamical model of the car following behavior using the solid angle and its change rate as variables for the first time so that we replace the original variables, such as the distance and velocity, by introducing the concept of solid angle into the previous classic car-following model. In Section 3, linear stability analysis is used to ascertain the critical stable condition of the traffic flow. Then the modified KdV equation is derived to analyze the nonlinear stability. In Section 5, numerical simulation is conducted to further explore the properties of the proposed model and the results are applied to investigate the phase transition characteristics. The results of in the above steps show different characteristics compared to previous models. As a consequence, we explain the critical phase transition from car-following the behavior based on solid angle caused by the effects of vehicle size.

2. Solid angle model

Most of the previous models were built if the assumption is founded that the drivers have accurate perception of the distance, velocity and acceleration of themselves and leading vehicles. However, there is no psychological evidence to support these assumptions. Previously we have proposed a visual angle model (VAM) to consider drivers’ visual perception behavior.[18] In this model we introduced the width of the leading vehicles only, which fails to completely describe the effect of the leading vehicles’ size.[19] Therefore, this paper introduces the concept of solid angle to establish the stability of the traffic flow influenced by the vehicle size.

In geometry, a solid angle is the angle of an object to a specific point in three-dimensional space, and it is an analogy of the planar angle. The solid angle describes the scale of the size of the object measured by the observer standing at a certain point. The apex of the solid angle is the point from which the object is viewed, and the object is said to subtend its solid angle from that point. In a car-following scenario, the apex of the solid angle is the following car driver, and the given object is the leading car.

A unit sphere is constructed with the observation point as its center. The projected area of any object projected onto the unit sphere is the solid angle of the object relative to the observation point. Therefore, the solid angle is an area on the unit sphere, which is similar to the planar angle being an arc length on the unit circle. A solid angle in steradians can be expressed by the following equation:

where A and r are the spherical surface area and radius, respectively, and Ω is the solid angle formed by A and r in the sphere.

Considering the sizes of leading vehicles and the solid angle of drivers, we replace the distance and speed in the original optimal velocity model by the solid angle and its change rate. To detect the vehicle movement, the solid angle is regarded as a stimulus, which depends on the leading vehicle size and the distance between the front bumper of the follower and the rear bumper of the leader, as shown in Fig. 1. Based on Eq. (1), the solid angle of the n-th driver is defined as

where Ωn (t) is the solid angle observed by the n-th driver at time t, Δ sn (t) is the space headway between the n-th vehicle and its leading vehicle, ln –1 is the length of the (n – 1)-th vehicle (the leader), and An –1 is the rear area of the (n – 1)-th vehicle.

Fig. 1. Driver solid angle and its calculation diagram in a car-following scene.

In this paper, we substitute the space headway and the velocity difference with the solid angle and its change rate, respectively. Then, we propose a novel model called the solid angle model, or SAM for short. The model can be formulated as

where U is the optimal velocity function, un (t) is the n-th vehicle’s velocity, α is the sensitivity parameter of the driver’s velocity, and λ is the sensitivity parameter of the change rate of the solid angle d Ωn (t)/d t. U[Ωn(t)] is a certain velocity a driver intends to reach in terms of the solid angle of the following vehicle called optimal velocity function (OV function for short). To compare the results intuitively, in the novel SAM we directly use the same OV function and similar parameters from the VAM[17] and FVD models.[21] Consequently, as a stimulation, the solid angle of the leading vehicle is also considered in the OV function, which is modified as

Therein, U1 = 6.75 m/s, U2 = 7.91 m/s, C1 = 0.13 m−1, and C2 = 1.57. The verification and calibration of U1, U2, C1, and C2 have been reported by Helbing and Tilch.[20]

The acceleration describing the solid angle stimulus and the following driver’s response is expressed in Eq. (3). Due to the effects of the leading vehicle size, the follower driver chooses to run with an optimal velocity with regard to the solid angle. Hence, the SAM is more realistic, as it uses the solid angle information as stimulus.

3. Linear stability analysis

Considering the stability of a steady traffic flow, it is assumed that all vehicles are dimensionally identical, moving at a uniform optimal velocity and distance headway. Therefore, the location of the n-th vehicle is

where is the steady position of the n-th car, n is the car number, h is the space headway at a uniform state, Ω0 = An–1/(h – ln–1)2 is the steady solid angle of drivers, and U(Ω0) represents the optimal velocity for the solid angle Ω0. These are all the parameters for describing a stable flow.

In order to explore the characteristics of SAM’s stability, a small disturbance is added to the steady state . The actual position of the n-th car is then expressed as

where rn (t) is a small disturbance of the n-th car.

Substituting Eq. (10) into Eq. (6), the solid angle can be rewritten considering the small disturbance as

where Δ rn (t) is the difference between the two small disturbances of the leading car and the following car. Ignoring the second-order term of Δ rn (t), the solid angle Ωn and its rate of change d Ωn/dt can be approximated by using the following equations:

Using the solid angle and its rate of change equations from Eqs. (12) and (13), the actual motion equation of the n-th car can be rewritten as

The small disturbance rn (t) is applied in the form of Fourier-modes rn (t) = μ exp (i kn + zt). Equation (14) then assumes the following form:

Here, z can be expressed as follow:

The equation of deriving neutral stability condition is z2 = 0. The parameters zi (i ≥ 3 and i ∈ N) can be neglected. The first- and second-order coefficients of z are obtained as follows:

As a result, the neutral stability condition is derived by

For a small disturbance rn (t), the traffic flow is stable when the sensitivity coefficient satisfies the following condition; otherwise, the steady-state traffic flow will develop into stop-and-go waves,

The linear stability conditions for different models are compared in Fig. 2. It is easy to see that a larger asymmetry can be observed clearly in SAM than VAM, which means that the full size of the leader has a greater influence on the follower. The results show that the SAM can better describe the influence of the vehicle size on stability and is more in line with actual driving behavior than previous models.

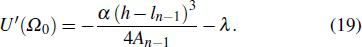
Fig. 2. Comparison of headway-sensitivity relationship diagrams with different car-following models.

The sizes of leading vehicles also influence the stability regions of SAM, as shown in Fig. 3. The typical sizes (length × width × height) for trucks and cars used in this paper are 10.0 m × 2.5 m × 3.0 m and 5.0 m × 1.8 m × 1.5 m, respectively. With a given headway, a leading truck will produce a larger solid angle than a leading car, which brings in a stronger psychological stress on the following driver and improves the stability of the traffic flow.

Fig. 3. Headway-sensitivity relationship diagram when following a car or truck.

Figure 4 presents the critical stability curves for different widths, heights, and lengths of the leading vehicles. When the width and height of the vehicles increase, the sensitivity apex declines and the critical stability region becomes larger. At the same time, when the length of the vehicle increases, the stability region does not change, but it shifts to the right instead.

Fig. 4. Headway-sensitivity relationship diagrams with (a) different widths of leading vehicles, (b) different heights of leading vehicles, (c) different lengths of leading vehicles.
4. Modified KdV equation

When the steady traffic flow is affected by a random disturbance, the change of the traffic flow state near the critical point will be transmitted to the upstream in the form of density wave. In this section, we obtain a nonlinear wave equation using the long wavelength mode to depict the propagation behavior so that we achieve the purpose of analyzing the slowly varying behavior at long waves.

Plugging Eq. (6) into Eq. (8), we can know that U[Ωn(t)] can be transformed to U[sn(t)] equivalently, so we make a corresponding transformation of Eq. (7) to Eq. (21) depicted as follow:

On the basis of Eq. (17), the expression of the (n + 1)-th car can be obtained as

Subtracting Eq. (17) from Eq. (18), we can get the following equation:

We use both space and time variables, and a constant b which is undetermined to define the slow variables as follows:

The headway is expressed as

and then equation (23) is expanded into the fifth-order of ε using Taylor method. We derive the equation as follow:

Here, the parameters mi are expressed as follows:

with

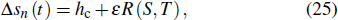
Under both conditions of αc = (1 + ε2)α and b = V′, the second-order and third-order terms of ε can be eliminated near the critical point (hc, αc). The simplified result is shown as follow:

where

For the purpose of giving a standard mKdV equation with infinitesimal of higher orders, we have to transform the variables as below:

The regularized equation can be worked out as follow:

The following expression is the target standard mKdV equation with the kink-antikink soliton solution omitting the O(ε):

Considering the correction term O(ε) and based on the solvability condition, the propagation speed c can be figured out and expressed with gi as follow:

Consequently, we can rewrite Eq. (30) as

and the amplitude of the solution is

The coexisting phase represented by the kink–antikink soliton solution is made up by the headways of the low-density free flow phase and high-density congested phase. The solution of the mKdV equation is an accepted expression for describing the state of traffic flow near the critical point, which is achieved by analyzing the nonlinear stability.

The neutral and coexisting curves with different lambdas are shown in Fig. 5. The headway-sensitivity space is divided into three parts, unstable, metastable and stable regions, respectively, by these two curves. All three parts exhibit asymmetrical characteristics in uncongested and congested conditions which is due to the drivers' acceleration and deceleration asymmetry.

Fig. 5. Headway-sensitivity relationship diagram under different lambdas.

Similar to the neutral curves, the coexisting curves also exhibit asymmetric characteristics. In the congested state, the stability region is smaller than that in the uncongested state because the drivers will pay more attention to changes in the size of the leading vehicles, and then make a more timely response. The results illustrate that using solid angle under the consideration of vehicle size can enhance the linear and nonlinear stability of traffic flow.

As shown in Fig. 5, the dashed curves are the coexisting stability curves derived by the modified KdV equation and the solid curves are the neutral stability curves derived by the linear stability analysis. For comparison, the values of lambda are different and the corresponding curves are also shown in Fig. 5.

5. Simulation

In order to further explore the properties of SAM, numerical results are presented to explore the characteristics of phase transition. In the simulations, the n th vehicle’s velocity and position are calculated using the following equations:

This simulation uses periodic boundary conditions. Initially, it is assumed that total N vehicles are on the lane under an even space headway. The initial speed of each vehicle is the optimal velocity based on the solid angle. Then, we give the first vehicle a small disturbance. The initial position of all vehicles can be expressed as

where N is the vehicle number equal to 100, and L is the length of the simulation circle road set to 1500 m.

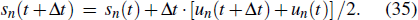
Kink-antikink density waves, which are an important feature of traffic congestion in the unstable region, are shown in Fig. 6. Even if the traffic flow is initially homogeneous, a small disturbance will slowly evolve and eventually lead to the stop-and-go waves. In Fig. 6, patterns (a), (b), and (c) represent three different unstable states, respectively, and as seen a small disturbance can quickly propagate and generate coexisting phases. When λ = 120, the effects of the solid angle become very large, which causes the density waves to disappear in Fig. 6(d). Therefore, λ characterizes the following driver’s ability to sense the change rate of the solid angle.

Fig. 6. Spatiotemporal evolution of the distance headway for different λ.

The asymmetric characteristics of the SAM can be easily observed in Fig. 7. A driver needs to spend more time accelerating from the congested condition to the free flow than decelerating from uncongested condition to congested flow. The essence is that drivers are more sensitive to the perception of collision risk. Our simulation indicates that the novel SAM can describe real driving behavior better.

Fig. 7. The stop-and-go waves in SAM.

Spatiotemporal vehicle trajectory diagrams also clearly exhibit the effects of vehicle’s size, as shown in Fig. 8. As the proportion of trucks rises, the stability of the traffic flow is enhanced. Due to the influence of solid angle, the truck ratio has a strong stabilizing effect. When the truck ratio reaches 20 %, the traffic flow changes to a freely moving phase. The simulation results indicate that trucks have an obvious effect on followers, stabilizing go-and-stop waves and increasing the road capacity.

Fig. 8. Spatiotemporal vehicle trajectory diagrams for different truck ratios.
6. Conclusions

The main contribution of this paper is to propose the influence of the solid angle on the car following theory. This allows us to take the size of leading vehicles into account, which is an issue hard to investigate in previous studies. The novel SAM is an improvement of the OV model. Stability analysis results indicate that the neutral and coexisting stability curves are asymmetric, and such that the steady and metastable regions are enlarged as the leading vehicle’s size increases. The SAM’s validity is also be verified through the corresponding numerical simulations, which show that the size of the leading vehicle strongly influences and enhances the stability of traffic.

Reference
[1] Helbing D 2001 Rev. Mod. Phys. 73 1067
[2] Bando M Hasebe K Nakayama A Sugiyama Y 1995 Phys. Rev. 51 1035
[3] Laura H 2017 Physica 348 44
[4] Peng G H Cai X H Liu C Q Cao B F Tuo M X 2011 Phys. Lett. 375 3973
[5] Zhao X M 2014 Physica 275 54
[6] Jin S Wang D H Tao P F Li P F 2010 Physica 389 4654
[7] Jin S Wang D H Yang X Y 2011 Trans. Res. Rec. 2249 7
[8] Lubor B Vladimir J 2008 Physica 237 28
[9] Khallouk A Echab H Ez-Zahraouy H Lakouari N 2018 Phys. Lett. 382 566
[10] Zheng Y M Cheng R J Ge H X 2017 Phys. Lett. 381 2137
[11] Xin Q Yang N Y Fu R Yu S W Shi Z K 2018 Physica 501 338
[12] Zhu W X Zhang H M 2018 Physica 496 274
[13] Zhao H Z Chen Q G W Shi W Gu T L Li W Y 2019 Physica 526 120990
[14] Ge H X Wu S Z Cheng R J 2011 Chin. Phys. Lett. 28 090501
[15] Jin Z Z Cheng R J Ge H X 2017 Chin. Phys. 26 110504
[16] Ye F Zhang Y 2009 Transp. Res. Rec. 2124 222
[17] Aghabayk K Sarvi M Young W 2015 Transp. Rev. 35 82
[18] Jin S Wang D H Huang Z Y Tao P F 2011 Physica 390 1931
[19] Zheng L He Z 2015 J. Mod. Phys. S 26 1550090
[20] Helbing D Tilch B 1998 Phys. Rev. 58 133
[21] Jiang R Wu Q S Zhu Z J 2001 Phys. Rev. 64 017101
[22] Sun Y Q Ge H X Cheng R J 2019 Physica 521 752
[23] Wang T Cheng R J Ge H X 2019 Physica. 533 121915
[24] Wang T Cheng R J Ge H X 2019 IEEE Access 7 174725