† Corresponding author. E-mail:
Project supported by the Fundamental Research Funds for the Central Universities, China (Grant No. 2018MS056) and the National Natural Science Foundation of China (Grant Nos. 11605055 and 11974108).
We investigate the non-Markovian effects on the entanglement transfer to the distant non-interacting atom qubits, which are embedded in a coupled superconducting resonator. The master equation governing the dynamics of the system is derived by the non-Markovian quantum state diffusion (NMQSD) method. Based on the solution, we show that the memory effect of the environment can lead to higher entanglement revival and make the entanglement last for a longer time. That is to say, the non-Markovian environment can enhance the entanglement transfer. It is also found that the maximum entanglement transferred to distant atoms can be modified by appropriately selecting the frequency of the modulated inter-cavity coupling. Moreover, with the initial anti-correlated state, the entanglement between the cavity fields can be almost completely transferred to the separated atoms. Lastly, we show that the memory effect has a significant impact on the generation of entanglement from the initial non-entangled states.
The non-classical property of quantum entanglement is one of the most important characteristics of quantum physics. It is beneficial to understanding of the basic theory of quantum mechanics and has potential applications in quantum information processing and quantum communication.[1] Faithful transfer of quantum state between two distant sites is an essential task in quantum technology, which can be realized either by teleportation or quantum networking.[2–5] In the past, cavity quantum electrodynamics (QED) that can be applied to study the interaction between atoms and quantized electrodynamics has been shown to be a promising and natural framework for the further study of entanglement control and manipulation.[6–11] The implementation of cavity QED architecture can be extended to the superconducting circuit systems, constructed by Josephson junctions and various electronic components, which is usually called circuit QED.[12] Generally, the superconducting qubit is often referred to as an artificial atom that can be designed for various research purposes. Hence, the solid-state superconducting circuits have been proved to be an efficient tool to realize quantum information processing, such as the implementation of entangled states,[13,14] quantum state transfer,[15,16] and quantum logic gates.[17]
However, the difficulties arise, e.g., any realistic quantum system will inevitably interact with its surroundings and thus leads to quantum disentanglement or limits the fidelity of quantum state transfer.[18] Many efforts have been devoted to finding approaches for entanglement protection in quantum open systems, such as quantum error correction,[19–21] quantum Zeno effect,[22] and dynamical decoupling.[23] Conventionally, when the system and environment are weakly coupled, the environment with short memory time can be regarded as Markovian dynamics. However, in many cases, the weak-coupling approximation is not applicable, thus the memory effect cannot be neglected, which corresponds to non-Markov process.[24–27] The effect of non-Markov process on decoherence and disentanglement of an open system is obviously different from the Markov process due to the back flow of information.[28,29] It has been shown that engineering structured non-Markovian environment is also meaningful to protect the system from the decoherence.[30–33]
In this paper, we focus on the influence of the memory effect on the entanglement transfer to the distant artificial atoms in non-Markovian reservoirs, from the master equation of the system derived by the NMQSD approach.[28,34–39] It is a newly developed technique in both analytical treatments and numerical simulations to solve non-Markovian dynamics of quantum open systems. Our results show that the environmental memory can lead to long-lasting and higher revived entanglement, thus the non-Markovian properties play a major role in the entanglement transfer and generation. Also, the impact of the modulated inter-cavity coupling on the entanglement transfer is studied.
The paper is organized as follows. In Section
The model we consider is composed of two coupled cavities, each of them also interacts with independent single qubit. The possible setup for the implementation of the scheme can be realized in a circuit QED system, as shown in Fig. 


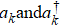
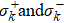
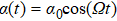
 | Fig. 1. Schematic of a circuit-QED design for our scheme. Two cavities interact via a SQUID-mediated tunable coupler, and each resonator mode is coupled to a superconducting transmon qubit. |
We assume that the system is coupled to a bosonic bath which can be described by

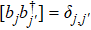

In the following we solve the model using the NMQSD approach. It can be proved that the full wavefunction of the total system including both the state of system and environment can be represented by a stochastic pure state called the quantum trajectory as follows:



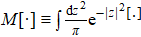

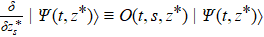

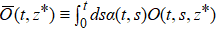
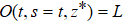
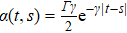

Actually, using the consistency condition









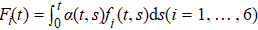


With the determined coefficient functions, the reduced density matrix of the system can be recovered by taking the statistical mean of all the generated trajectories,


Having developed the time-local non-Markovian QSD equation for the system, we now concern about the entanglement generation and entanglement transfer from the cavity modes to the atom qubits. Throughout this paper, we employ the well-known concurrence measure defined by Wootters to quantify the degree of entanglement for any two-qubit system, which can be expressed as[44]


In Eq. (

We are now able to investigate the state transfer performance from cavities to the separated atom qubits. We assume that there is at most one excitation in the system since we are interested in the dynamics of entanglement transfer at zero temperature. Initially we have non-entangled atom qubits and entangled photons. For instance, we choose the two cavity modes prepared in one of their Bell states 

 | Fig. 2. The time evolution of the entanglement transfer. The initial state is prepared in  |
In order to analyze the influence from the non-Markovian environment on the entanglement transfer, we plot the time evolution of the two-atom entanglement for different memory times indicated by 1/γ, as shown in Fig. 
Apart from the memory time, some other parameters of the system also play an important role in the entanglement dynamics. Therefore, in order to achieve higher entanglement transfer, it is truly important to tune the parameters to certain optimal values in the actual experiment. In the following, we investigate the influence of some parameters such as the modulated inter-cavity amplitude and frequency on the entanglement transfer. In Fig. 

 | Fig. 4. Two-atom entanglement for different inter-cavity coupling frequencies Ω. The initial state is prepared in  |
In Fig. 
 | Fig. 5. Two-atom entanglement for different inter-cavity coupling amplitudes α0. The initial state is prepared in  |
Finally, we consider the performance of the entanglement generation. Initially we have both non-entangled atoms and non-entangled photons. Figures 
In summary, we have studied the dynamics of the entanglement transfer to the distant atom qubits, which are embedded in two separated lossy cavities connected by SQUID-mediated tunable coupler. Actually, the cavities are coupled to a non-Markovian environment instead of a Markovian one. A general master equation for the concerned system can be obtained by the NMQSD approach. We first analyze the influence of the memory effect on the entanglement transfer under the rotating-wave approximation. It is found that the longer memory time is helpful for entanglement transfer, and the non-Markovian effect will lead to a stronger entanglement revival phenomenon. Another major procedure is that the coupling between two resonator modes is time-dependent, which can be realized by modulating the inductance of the SQUID. Also, it helps to optimize the maximum entanglement transferred to the atoms by appropriately selecting the frequency of the inter-cavity coupling. In addition, we show that the entanglement of the resonator modes with the initial anti-correlated state can be almost completely transferred to the atoms. Finally we investigate the non-Markovian effects on the entanglement generation with initial separated sates.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] |





