† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51776037 and 51806147) and Natural Science Foundation of Jiangsu Province, China (Grant No. BK20170082).
The fractal Brownian motion is utilized to describe pore structures in porous media. A numerical model of laminar flow in porous media is developed, and the flow characteristics are comprehensively analyzed and compared with those of homogeneous porous media. Moreover, the roles of the fractal dimension and porosity in permeability are quantitatively described. The results indicate that the pore structures of porous media significantly affect their seepage behaviors. The distributions of pressure and velocity in fractal porous media are both non-uniform; the streamline is no longer straight but tortuous. When Reynolds number Re < 1, the dimensionless permeability is independent of Reynolds number, but its further increase will lead to a smaller permeability. Moreover, due to the higher connectivity and enlarged equivalent aperture of internal channel network, the augment in porosity leads to the permeability enhancement, while it is small and insensitive to porosity variation when ε < 0.6. Fractal dimension also plays a significant role in the permeability of porous media. The increase in fractal dimension leads to the enhancement in pore connectivity and a decrease in channel tortuosity, which reduces the flow resistance and improves the transport capacity of porous media.
Porous media are composite materials consisting of solid skeleton and pores with various sizes and shapes. Seepage phenomena in porous media are widely observed in nature and practical applications, such as water transport in soil,[1] oil and gas exploitation,[2] and drug delivery in vascular networks.[3] Existing studies have documented that the permeability characteristics of porous media depend on their pore structures and the physical properties of transported fluids.[4–6] However, since the pore distribution in most porous media is extremely intricate in reality, which includes interconnected and intricate channel network and pores with different sizes and shapes, it is still of great challenge to predict the seepage behavior accurately, and the quantitative relationship between structure parameters and permeability of porous media also needs to be further studied.
Scholars have carried out a lot of experimental[7,8] and theoretical[4,5,9] studies on the permeability characteristics of porous media for a long time. Most of the early research results are based on semi-empirical models, such as the Dacy model,[10] Brinkman–Forchheimer model,[11] and Kozeny–Carman model. Nevertheless, these models all contain empirical constants with no specific physical significance, which fails to characterize the seepage characteristics of porous media further. Moreover, due to the intricate internal channel network, the seepage behavior in porous media includes the intricate micro-boundary effect and the interaction between the solid matrix and fluid phase. Therefore, the available theoretical models can only predict the flow behavior in porous media with simple or regular structures. For irregular porous media, they are directly or indirectly regarded as a virtual continuum medium with uniform distribution on a large scale in practical applications. It is nearly impossible to describe the real pore structure of porous media accurately, but only to qualitatively demonstrate the internal flow behavior on a large scale rather than to reveal the micro-scale flow characteristics in porous media.
Due to the pioneering work of Mandelbrot,[12] the fractal theory has been widely applied in the investigations of heat and mass transfer in porous media in the last decades.[4,13,14] The introduction of fractal theory not only opens up a new way for the description of the irregular porous media but also makes it possible to reveal the percolation mechanism of porous media in depth. Pitchumani et al.[15] presented a fractal model of permeability without empirical constants during the research on percolation characteristics of porous fiber fabrics, which pioneered the introduction of fractal geometry to predict the flow behavior in porous media. Miao et al.[16] presented a fractal permeability model for the porous media, which is a function of the tortuosity fractal dimension, pore area fractal dimension, dimensionless pore size, and dimensionless pressure difference. Shen et al.[17] numerically studied the permeability in porous materials reconstructed by Sierpinski carpet based on a fractal model. Chen et al.[4] conducted a numerical study on seepage characteristics in fractal porous media constructed by Sierpinski carpet. The results indicated that the pore structure and connectivity plays a significant role in the permeability of porous media with identical porosity. However, most of the available fractal models for the construction of porous media are based on self-similar structure such as the Sierpinski carpet[4,17,18] and Menger sponge[19] (i.e., the fractal dimension is constant), which fails to demonstrate the randomness of pore structure in porous media. Kikkinides et al.[20] constructed a binary medium with both characteristics of randomness and statistical self-similarity based on the fractal Brownian motion (FBM). On this basis, a multi-dimensional fractal porous medium is developed by Türk et al.[21] via associating the stochastic function following the statistical characteristics of FBM with the properties of porous media. As a typical stochastic fractal model, FBM has proved its outstanding value in various practical applications, including terrain reconstruction,[22] pollutant diffusion,[23] and picture processing.[24] Kikkinides et al.[25] developed a binary medium generation method for generation of three-dimensional porous media based on the FBM model and validated its reliability by comparing the numerical predictions with the actual experiment for the permeability of the sandstone. Ma et al.[26] reconstructed the two-dimensional and three-dimensional porous media by the FBM model, and numerically investigated the gas diffusion characteristics in the porous media. Their results indicated that the numerical results of the effective diffusion coefficient agreed well with the experimental measurement. These previous research results have proved the practicability of the FBM method for construction of porous media with complex structures. Therefore, it is feasible to investigate the permeability characteristics of fractal porous media generated by the FBM method.
Based on a deep understanding of the FBM, a fractal model with an adjustable fractal dimension is developed to describe the solid matrix distribution of porous media quantitatively. With the reconstruction of fractal porous media, the mathematical model of single-phase fluid in fractal porous media is established and numerically studied with high priority to the role of solid matrix distribution in permeability characteristics. The flow characteristics in fractal porous media are compressively discussed and compared with those in homogeneous porous media, and the roles of fractal dimension and porosity in permeability characteristics of fractal porous media are quantitatively described.
The pore distribution and the solid matrix of most porous media are usually multi-scale, random, and statistically self-similar,[27–29] which is hard to describe by the traditional Euclidean geometry. Thanks to the pioneering work of Mandelbrot[12,29] and Kikkinides,[20] fractal geometry becomes an attractive application for characterizing porous media due to its intrinsic property of self-similarity. In their theory, the irregularity of pore distribution for porous media is quantitatively described by the fractal dimension.[20] Due to its outstanding merits in fractal description, the applications of the FBM model for porous media reconstruction are validated in the investigation of thermal conduction and mass transport.[30] Therefore, FBM is applied to reconstruct the solid matrix of porous media.
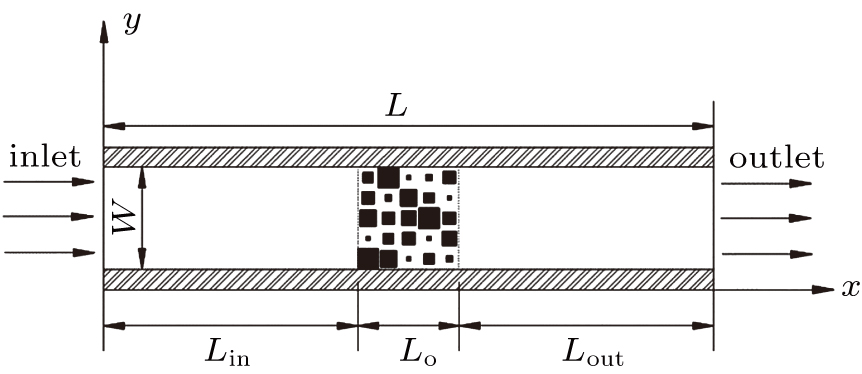
Due to its complex pore structure, the porous medium here is assumed to be two-dimensional, which is usually available in the literature.[4,20] A recursive method based on the random midpoint displacement algorithm is applied to describe the solid matrix distribution in the porous medium. A random function fH(r) is defined as the methodology obeying FBM statistical properties. In this study, r represents the displacement and H is the Hurst exponent. In this methodology, the solid particle of porous media is regarded as a square, and its size is specified by fH(r). Figure Four solid particles are arranged at the corners of the square (see Fig. Then, the particle size at the square center shown in Fig.


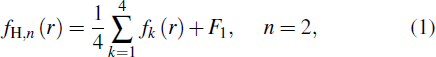



Calculate fH,3(r) for the particle size at the edge midpoints (see Fig. 
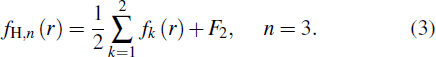


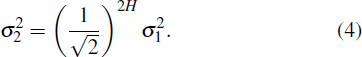
Repeating the above steps (2) and (3) with a scaling factor 
The statistical self-similarity of FBM depends on the Hurst exponent, which herein determines the spatial distribution of solid matrix for the fractal porous media as well. Moreover, the fractal dimension of the two-dimensional porous media relies on the Hurst exponent, D = 2 – H. For further understanding of the fractal dimension, Fig.
Due to the merits of randomness and the statistical self-similarity of FBM, the solid matrix of the two-dimensional fractal porous medium is reconstructed herein. Water is used as a working medium, and its physical properties are listed in Table
| Table 1. Physical parameters of water. . |
For simplification of the numerical solution, serial assumptions should be made in this paper: (1) Steady laminar flow. (2) The liquid–solid interface is the no-slip boundary. (3) The physical parameters of the fluid are constant. (4) The mass force item is ignorable.
It has been documented that the liquid flow in porous media such as oil and gas exploitation, groundwater infiltration, and blood flow in the vascular network can be assumed to be laminar flow, in which the Reynolds number of internal flow is small.[31] Based on these assumptions, the governing equations for laminar flow in our porous medium can be given by the continuity equation


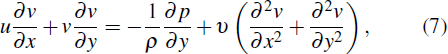
The volume flow rate at the inlet of the channel is regarded as constant. Therefore, the constant velocity condition is set to be the inlet boundary condition, which can be written as



In the present work, the commercial CFD software Fluent is used to study the seepage characteristics of the two-dimensional porous medium. To acquire the velocity and pressure distribution of fluid in the porous medium, the governing equations are solved by the finite volume method with a dual-precision solver. The momentum equation and pressure term are discretized by the second-order upwind scheme, and the convection term is discretized by the fully implicit mixed difference scheme. Moreover, the SIMPLE algorithm is utilized to determine the pressure-velocity coupling. A series of discrete equations in terms of velocity and pressure can be obtained by integrating the discretized equations in each control volume. For better convergence accuracy of the calculation, the Gauss–Seidel method considering the over-relaxation factor is applied to solve all the discrete equations. The iteration is regarded to be convergent when the maximum residuals of velocity and pressure after iteration are both less than 10–6. Furthermore, the iterative calculation can also be considered to be converged when the average velocity at the channel outlet remains constant.
To perform the numerical solution based on the present model, a structured grid system is used to divide the computational domain, as shown in Fig.
 | Fig. 5. Effect of number of nodes on velocity distribution in the porous medium (ε = 0.7): (a) Nn = 62425, (b) Nn = 125446, (c) Nn = 170821, (d) Nn = 188964. |
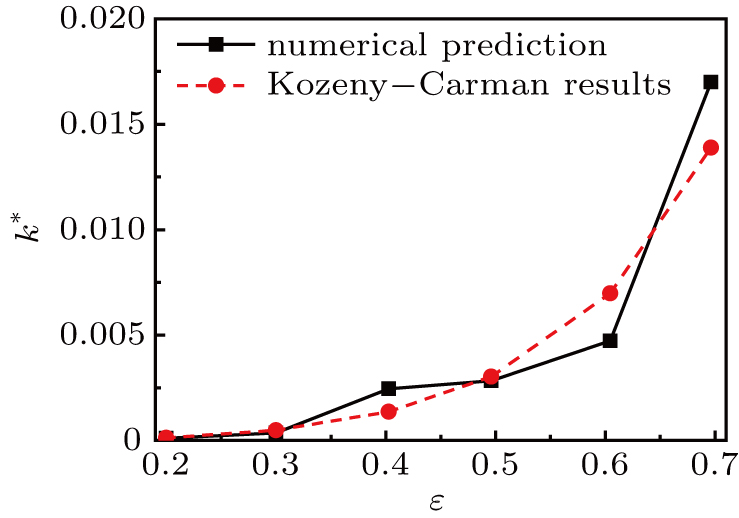
To verify the present model, a numerical investigation on the liquid flow in the two-dimensional porous medium with different porosities is conducted here. The numerical results from the current model are compared with those of the Kozeny–Carman equation[32]

A comparison between the numerical predictions and the Kozeny–Carman results for the dimensionless permeability in the two-dimensional porous medium is given in Fig.
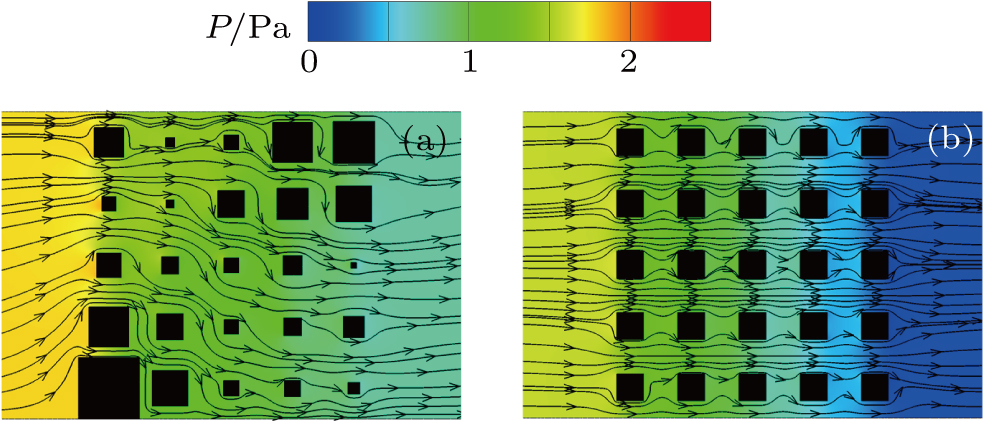
The randomness of the pore structure makes the channel network in the porous medium very complex. Fluid flows in interconnected pores are distorted, which has a significant impact on the permeability characteristics of the porous medium. To reveal the percolation mechanism in the porous medium, Fig.
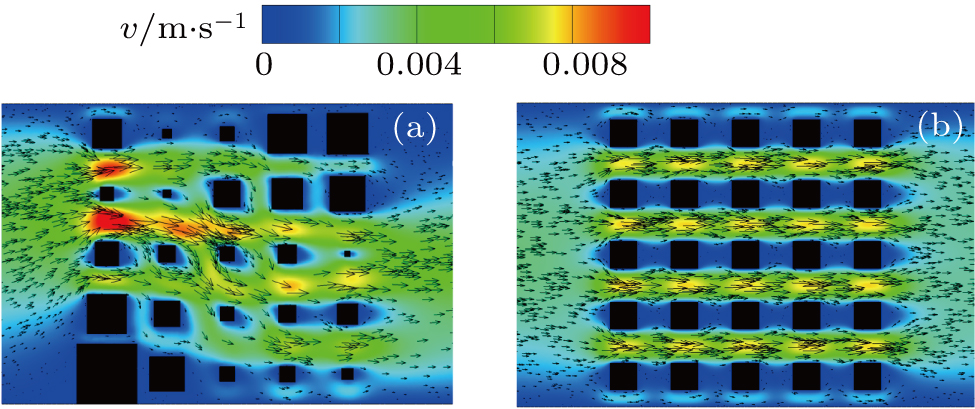 | Fig. 8. Velocity and vector distribution in the fractal and homogeneous porous medium (ε = 0.8): (a) fractal porous medium, (b) homogeneous porous medium. |
To further understand the effect of solid matrix distribution on the flow characteristics, the pressure distribution and streamline diagrams in the fractal and homogeneous porous medium are demonstrated in Fig.
It has been documented that when the Reynolds number is low, the liquid flow in the porous medium agrees well with the Darcy law.[33] In general, the permeability is utilized to characterize the percolation behavior in the porous medium. However, it usually depends on the dimension of the porous medium, which fails to reveal the inherent characteristics of percolation. Therefore, the dimensionless permeability is introduced to describe the transport capacity of the porous medium. The dimensionless parameter is calculated by


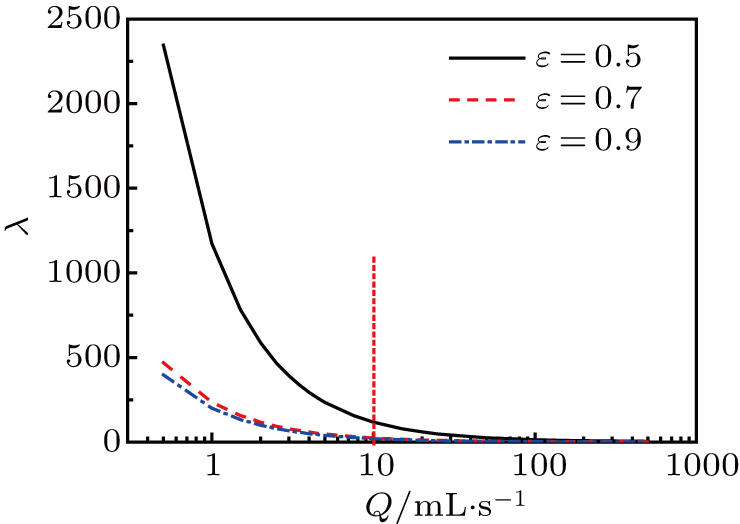
Previous studies have shown that Darcy’s law can only be applied when the percolation rate is small.[33] With the increase of percolation rate, the flow characteristics in the porous medium will gradually deviate from Darcy’s law. To determine the range of percolation rate in which flow characteristics satisfy the Darcy law, the seepage behaviors in the porous medium are analogized to these in tubes. Here the Reynolds number can be written as




The relationship between the volume flow rate and the friction drag coefficient is illustrated in Fig.
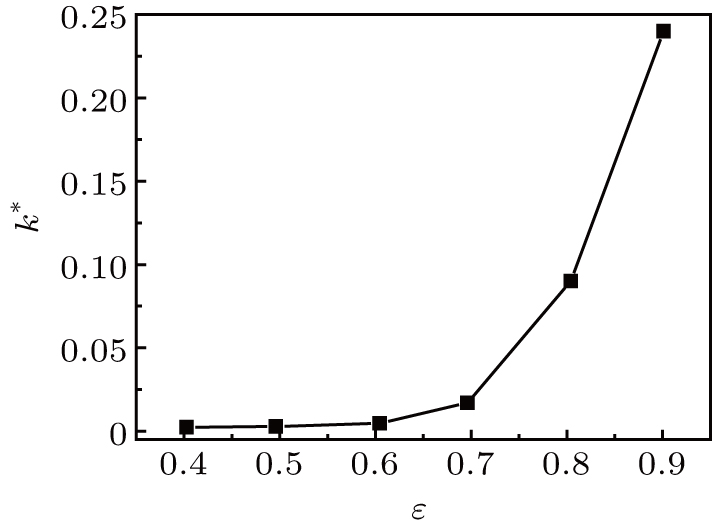
As one of the important structural parameters, porosity visually presents the pore occupancy of the porous medium, which plays a significant role in the seepage performance of the porous medium. On account that the pores of the porous medium considered in the current work are interconnected, the increase of porosity contributes to higher connectivity and enlarged equivalent diameter of the internal channel network, enhancing the permeability of the fractal porous medium. To study the role of porosity in the permeability of the fractal porous medium, Fig.
Figure
The fractal dimension of the porous medium constructed by the FBM model is applied to characterize the structural correlation of pores or solid matrix in the porous medium to some extent.[20,21] The pore structure in the fractal porous medium varies with the fractal dimension. Consequently, the fractal dimension significantly affects the seepage characteristics of the fractal porous medium as well though the porosity is identical. The dimensionless permeability of the fractal porous medium with different fractal dimensions is illustrated in Fig.
For further insight into the role of fractal dimension in the seepage characteristics of the porous medium, Fig.
The fractal Brownian motion (FBM) model is utilized to quantitatively describe and reconstruct the porous structure of a porous medium in the present work. The numerical model of liquid flow in the porous medium is developed and solved with emphasis on the role of solid matrix distribution. The flow characteristics in the fractal porous medium are analyzed and compared with those in the homogeneous one, and the roles of the fractal dimension and porosity in the seepage characteristics of the porous medium are given as well. The conclusions are summarized as follows:
The pressure and velocity distributions in the fractal porous medium are non-uniform due to the tortuous internal channels and different aperture sizes. The streamline in the fractal porous medium is no longer a straight line but a tortuous curve. Along the flow direction, the velocity in the large aperture channel is larger, and the peak velocity appears in its throat, while the velocity in the narrow channel is small, and the velocities in the wake region of some large solid particles are nearly zero. There is a transition point in the influence of Reynolds number on dimensionless permeability of the porous medium. When Re < 1, the dimensionless permeability of the fractal porous medium remains constant. However, with the further increase of Reynolds number, the dimensionless permeability decreases gradually, which indicates that it is impossible to use Darcy’s law to accurately predict the seepage behavior in the porous medium when Re > 1. Porosity is an important factor affecting the seepage characteristics of the porous medium. The permeability of the fractal porous medium increases monotonously with the increase of porosity due to the higher connectivity and enlarged equivalent aperture of the internal channel network. It is interesting that the dimensionless permeability only has a slight variation when ε < 0.6, while a further increase in porosity leads to a rapid augment in the dimensionless permeability of the porous medium. Though the porosity is identical, the fractal dimension also plays a significant role in the seepage characteristics of the porous medium. The structural correlation of the solid matrix in the porous medium decreases with the augment in the fractal dimension. In this study, the connectivity of channel network in the porous medium is enhanced, and the channel tortuosity is decreased, which reduces the flow resistance loss and augments the transport capacity of the porous medium.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |