† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11772141 and 11262019) and the State Scholarship Fund of China Scholarship Council (Grant No. 201708370030).
Biological growth is a common phenomenon in nature, and some organisms such as DNA molecules and bacterial filaments grow in viscous media. The growth induced instability of morphoelastic rod in a viscous medium is studied in this paper. Based on the Kirchhoff kinetic analogy method, the mechanical model for growing elastic thin rod in the viscous medium is established. A perturbation analysis is used to analyze the stability of the growing elastic rod in the viscous medium. We apply the results into planar growing ring and get its criterion of instability. Take the criterion into DNA ring to discuss the influence of viscous resistance on its instability.
Growth is a common phenomenon in natural world. Growth means changing in mass in biology. Because growth can induce stress and stress inversely can affect growth, so during process of growth except mass varying structure and material character also along with varying. More evidence indicates that mechanical factor plays an important role in pattern formation of biological body,[1] such as many structures across scales from cell to tissue like neuron to brain.[2–5] Growth induced deformation is equivalent to constraint induced deformation. For example, convolution formation during developing of brain is affected by the skeletal constraint or different growth.[6]
Elastic rod or filament plays an important role in engineering and biological field. It can model many structures like undersea cable, sperm, bacteria, fungi, hair and so on.[7–10] In recently past years, the elastic rod model has attracted a great deal of attention from researchers since elastic rod has successfully modeled the helical structure of DNA.[11] Since DNA structures can be seen as an elastic rod model, quantitative methods can be applied to analyze its helical structures and dynamic behavior related to its function.[12,13] Based on the Kirchhoff elastic rod model, Goriely and Tabor developed a new perturbation scheme that is suitable for analyzing dynamic instability of filament.[14,15] Liu and Xue[11,16] studied thin elastic rod nonlinear mechanics of the DNA model. Xue et al.[17,18] developed the analytical mechanic theory of elastic rods. Furrer et al.[19] studied the relationship between the intrinsic shape and the existence of multiple stable equilibria within the context of DNA rings based on the Kirchhoff elastic rod model. Shi et al.[20] derived a generalized one-dimensional time-independent nonlinear Schrö dinger equation for the stationary state configurations of supercoiled DNA. Wang et al. studied symmetries and conserved quantities of Kirchhoff and Cosserat elastic rods.[21–23] Since many living things such as cell, sperm, and DNA are in fluid environment, viscous action should be taken into consideration in research of their mechanical behavior. Wolgemuth et al.[8] studied dynamic supercoiling bifurcation of Bacillus subtilis in fluid using the filament model to explain complex supercoiled structures during cells growth. Liu and Sheng[24,25] investigated the stability of elastic rod without growth in a viscous medium. Wang et al.[26] used the perturbation method to study the influence of viscous action on the dynamic instability of the elastic rod. The study on instability of growing elastic rod in viscous media is an alternative way to understand how the growth and viscous resistant couple to affect structures of living things in biology.
In this paper, we adopt the mophoelastic rod model. The arrangement of this paper is as follows. In Section
As discussed in Ref. [15], usual methods can result in an inconsistent perturbation scheme, so we will follow the method in Ref. [15]. The main idea of the coordinate base vector perturbation scheme is to perturb the principle axis coordinate base vectors and maintain orthogonality of new base vectors in order to make arc length conservative. That is, for any order perturbation εn, satisfying ei ⋅ ej = δij. Thus the new basis vector can be expressed in the unperturbed basis as



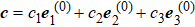


For a vector 

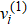
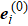
We introduce three configurations for different states of the growing elastic rod.[27] Initial configuration is the unstressed state at the initial time t = 0 and the superscript 0 indicates the quantities of this state. For example, the arc length of rod centerline can be written as s0 in initial configuration. Reference configuration is the state that the rod grows without constraints, so that at any given time t, it is in an unstressed state. This state is not realized in the experiment, so it is also called the virtual configuration and the superscript g is used to indicate the quantities of this state. The arc length of rod centerline can be written as sg in reference configuration. Current configuration is the true state of the growing rod at time t considering exterior load, body force and boundary conditions affections. The quantities in current configuration has no superscript. The arc length of rod centerline can be written as s in current configuration.
We define growth stretch as



Due to the slow-growth process, it is assumed that the growing rod in the unstressed state is always in equilibrium. In the reference configuration, the force and moment equilibrium equations of the elastic rod can be written as







Consider that the position of a material point on the centerline is 











We suppose that only the length of rod varies during growth, but maintains the cross section being constant, so we have the following dimensionless form:





Expanding Eq. (




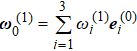

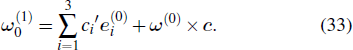







A classic problem in the theory of elastic rod is the buckling of a planar twisted ring to a non-planar configuration which was first considered in Refs.[31,32]. We take this problem as an example. Consider an growing elastic ring with radius 1 and cross-sectional radius a in the initial unstressed state. It is assumed that it grows linearly in time meaning γ = 1 + mt and keeps all other material properties unchanged. In initial configuration, the initial length of the ring is L = 2 π γ, where γ = 1 and initial curvature-twisting vector is 
We consider the buckling of the ring at time t. The radius of the ring is γ and the curvature-twisting vector is 









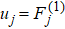


Equation (



We apply the result into a DNA ring. The classical parameter value of length L and radius a of cross section of the DNA ring are L ∼ 5 × 10–6 cm and a ∼ 10–7 cm.[33] The viscosity of the nucleoplasm is measured to be 25 ∼ 1000 Pa⋅s.[34] Thus we can calculate the value range of viscous drag coefficients in nucleoplasm to be ς ∼ [1.2, 96], ςR ∼ [15, 1200]. As we take γ = 2 and Γ = 1, it is unstable state, and relations of σ2 and mode number n with different viscous resistance coefficients are shown in Fig.
Since most living things live in viscous medium environment, instability of growing rod in a viscous medium has been analyzed in the present paper. The dynamics model of growing rod in the viscous medium and its dynamics equations are constructed. A system of linear differential equations is deduced by a new perturbation scheme to analyze stability of growing rod in the viscous medium. Taking planar growing ring as an example, we obtain its bucking criterion of growth stretch. We can conclude that viscous resistance has no effect on stability of growing ring but has remarkable effect on instability of growing ring. Applying the results into a DNA ring, we obtain a sketch about growth ratio σ and mode number n, from which can read the affection of viscous resistance on instability of growing DNA ring.
In the near future, we will investigate how the geometrical structure of growing ring in the viscous medium changes beyond buckling and analyze the exact geometrical structure by nonlinear analysis and numerical simulation.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |


