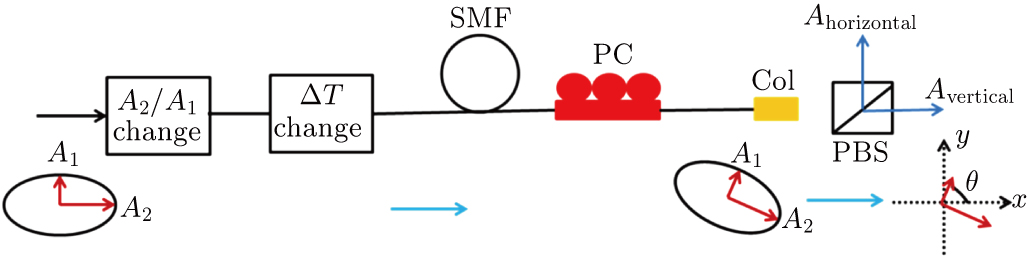
† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2018YFB0504500) and the National Natural Science Foundation of China (Grant No. 51672177).
We simulate pulse shaping of bright–dark vector soliton pair in an optical fiber system. Through changing input pulse parameters (amplitude ratio, projection angle, time delay, and phase difference), different kinds of pulse shapes and spectra can be generated. For input bright–dark vector soliton pair with the same central wavelength, “2+1”- and “2+2”-type pseudo-high-order bright–dark vector soliton pairs are achieved. While for the case of different central wavelengths, bright–dark vector soliton pairs with multiple pulse peaks/dips are demonstrated with appropriate pulse parameter setting.
Optical soliton is a kind of localized nonlinear wave in nonlinear optical systems, and it can propagate along long distances without pulse shape distortion. Optical solitons have been widely studied theoretically and experimentally. In theory, soliton solutions can be obtained by solving nonlinear Schrödinger equation (NLSE) and Ginzburg–Landau equation (GLE).[1] When the amplitude modulations (including gain, loss, spectral filtering, and saturable absorption) in GLE are negligible, GLE can be approximated with NLSE. While in experiments, optical solitons can be achieved in passively mode-locked solid-state and fiber lasers. Especially, solitons in ultrafast fiber laser field have been attracting much attention, because of the unique characteristics (including dispersion, nonlinearity, gain, and loss) offered by single-mode and multi-mode fibers. Currently, many researches are focused on optical solitons in single-mode fiber lasers, because of their compactness, stability, ease of maintenance, and so on. Until now, different kinds of optical solitons that exist in fiber lasers have been theoretically solved and experimentally demonstrated, such as traditional soliton,[2,3] dispersion-managed soliton,[4,5] self-similariton,[6,7] dissipative solion,[8,9] dual-wavelength domain wall soliton,[10] and so on.[11–14] They can be generated by appropriate design of intra-cavity parameters. Also, multi-state solitons can be emitted in bidirectional mode-locked fiber lasers.[15] As the development of detection techniques, soliton dynamics can be explored with time-stretch dispersive Fourier transform (TSDFT) technique,[16–19] which reveals the transient dynamics of soliton evolution and building processes.
In reality, single-mode-fiber is anisotropic even with circular symmetry, because of material imperfections and external environmental disturbance (such as stress and heat flow). So scalar approximation is not applicable and coupled NLSEs and GLEs should be considered for solving.[20] In this situation, various vector solitons could be generated, such as polarization/phase-locked vector soliton (PLVS),[21–23] group-velocity-locked vector soliton (GVLVS),[24–27] polarization rotation vector soliton (PRVS),[28,29] and so on, depending on the strength of intra-cavity linear birefringence and cross-phase modulation (XPM). Also, we can classify the vector solitons according to their pulse waveforms, such as bright–bright vector soliton, bright–dark vector soliton and dark–dark vector soliton. Bright soliton has a temporal intensity peak, while dark soliton has a temporal intensity dip with continuous light background. Vector solitons have potential applications in optical communications and optical data processing.[30,31]
In previous works, many different kinds of vector solitons have already been observed in mode-locked fiber lasers. For example, coherently and incoherently coupled bright–dark vector solitons in single-mode fiber lasers were experimentally shown.[32,33] Simulation about generating pseudo-high-order polarization-locked vector soliton was reported.[34] Manipulation of polarization- and group-velocity-locked dark vector solions was also theoretically simulated.[35] However, there are few reports about the pulse shaping of bright–dark vector soliton pair. In this paper, we simulate the pulse shaping of bright–dark vector solion pair in a polarization insensitive optical fiber system. Through changing input pulse parameters, different kinds of pulse shapes and optical spectra in orthogonal polarization directions can be generated. Our simulation result further explore the vector properties of optical soliton, and can provide beneficial conduct for latter experiments about pulse shaping of bright–dark vector soliton pair at different wavelengths.
Figure
Firstly, the temporal pulse amplitudes A1(t) and A2(t) of incident bright–dark vector solion pair in orthogonal polarization directions can be expressed as
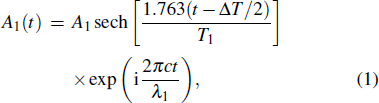
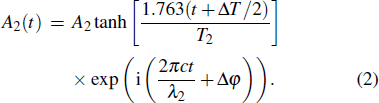

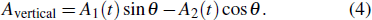
In the latter simulation, we let T1 = T2 = 5 ps and simulate the temporal pulse shapes and optical spectra of output horizontal and vertical polarization modes, through changing amplitude ratio, projection angle, time delay and phase difference for orthogonal modes. The simulation results include two parts: the first is considering orthogonal modes with the same central wavelength, and the second one considers those with different central wavelengths.
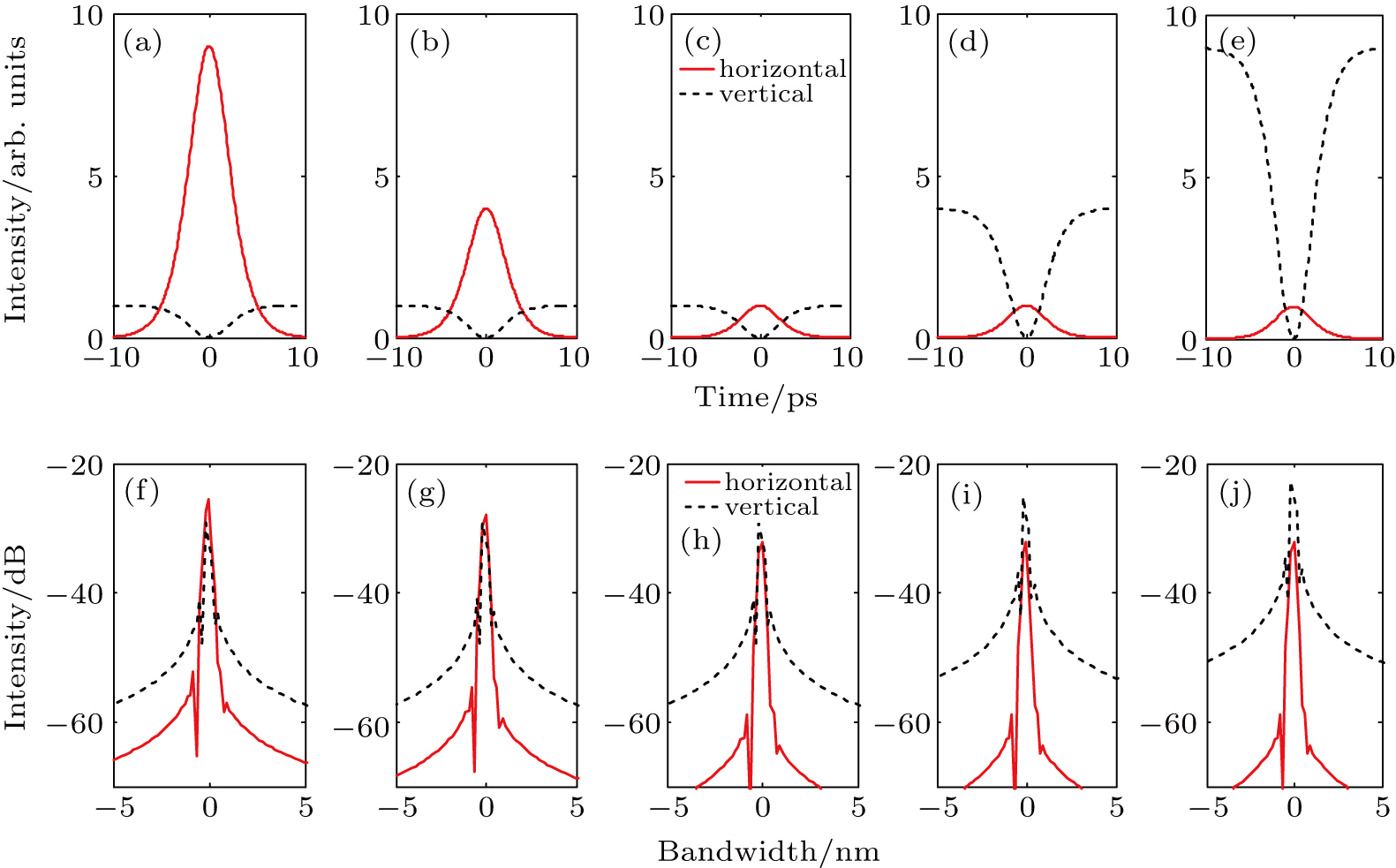
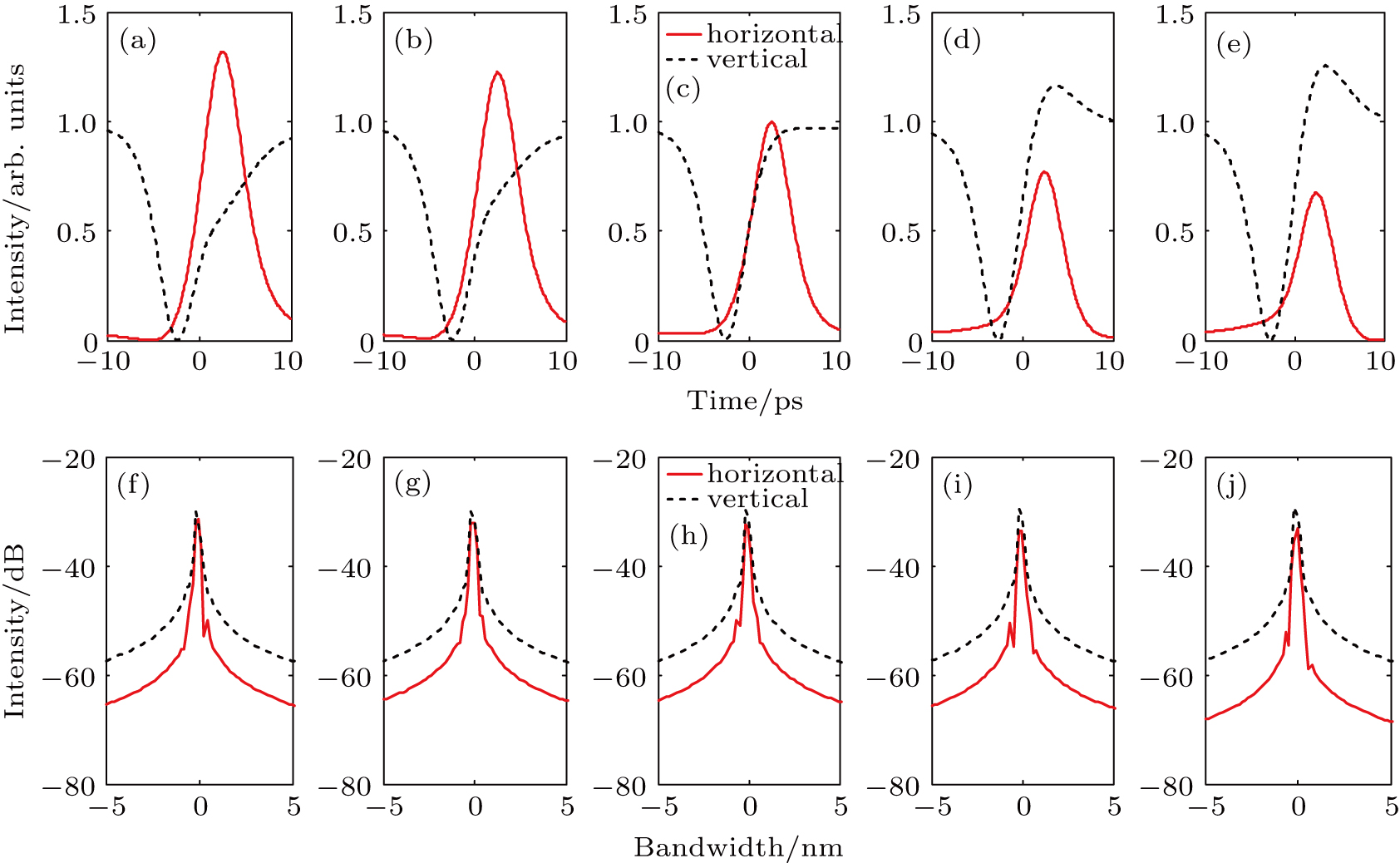
In this section, we assume λ1 = λ2 = 1064 nm. The 1064-nm central wavelength is selected because it can be generated in Yb-doped mode-locked fiber laser experimentally. Firstly, we consider the case when input amplitude ratio of bright–dark soliton pair is changed, and the corresponding simulation result is shown in Fig.
Then, we consider the change of projection angle θ. Other variables are: A1 = A2 = 1, ΔT = 3 ps, and Δφ = π/2. In Figs.
After that, we simulate the pulse shapes and optical spectra when time delay ΔT is changed from 1 ps to 10 ps. Others are: A1 = A2 = 1, θ = 10°, and Δφ = π/2. The corresponding simulation results are demonstrated in Figs.
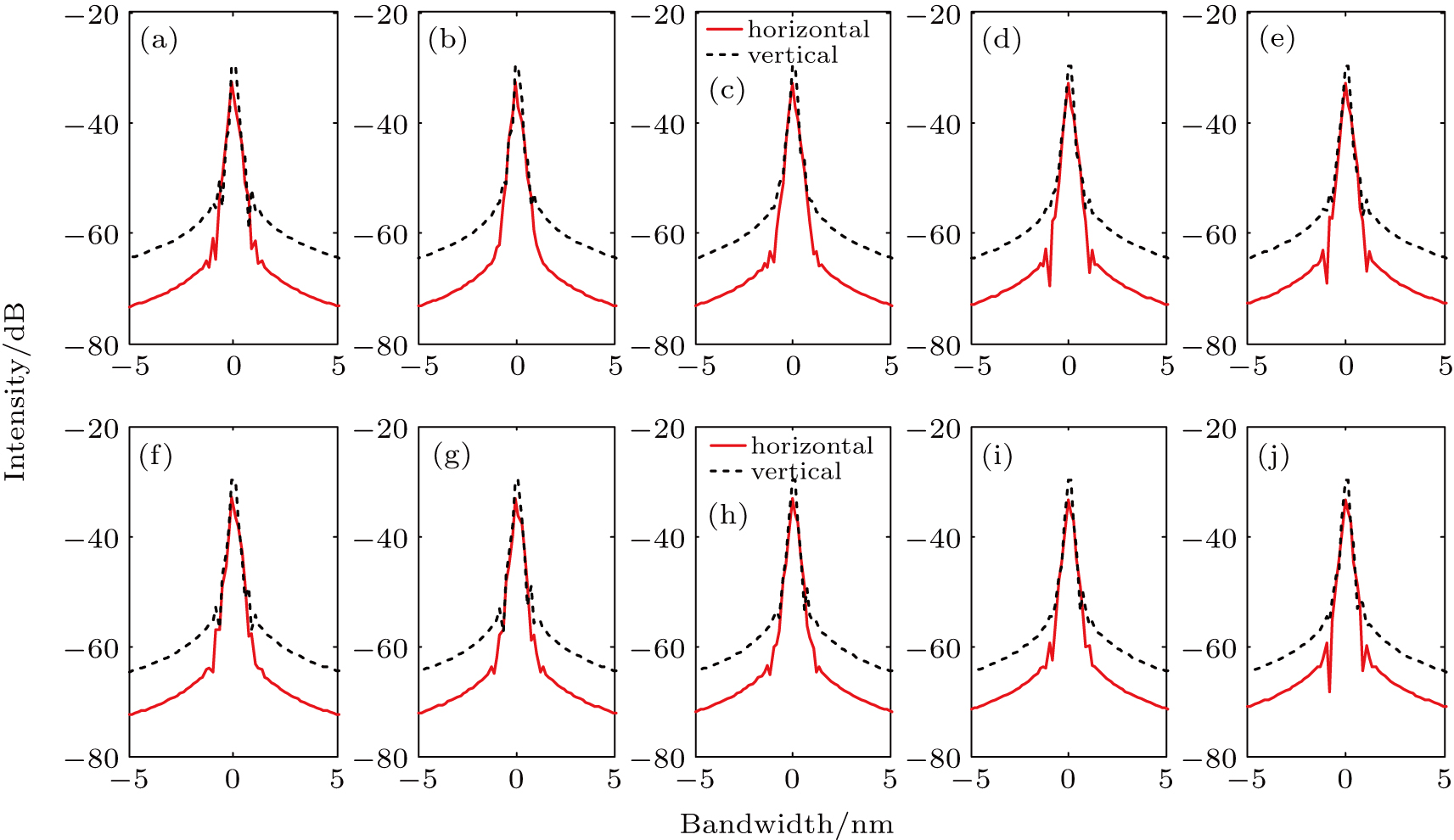 | Fig. 5. Simulated output optical spectra [(a)–(j)] in orthogonal polarization directions when time delay ΔT increases from 1 ps to 10 ps (1-ps time interval). Others are the same as those in Fig. |
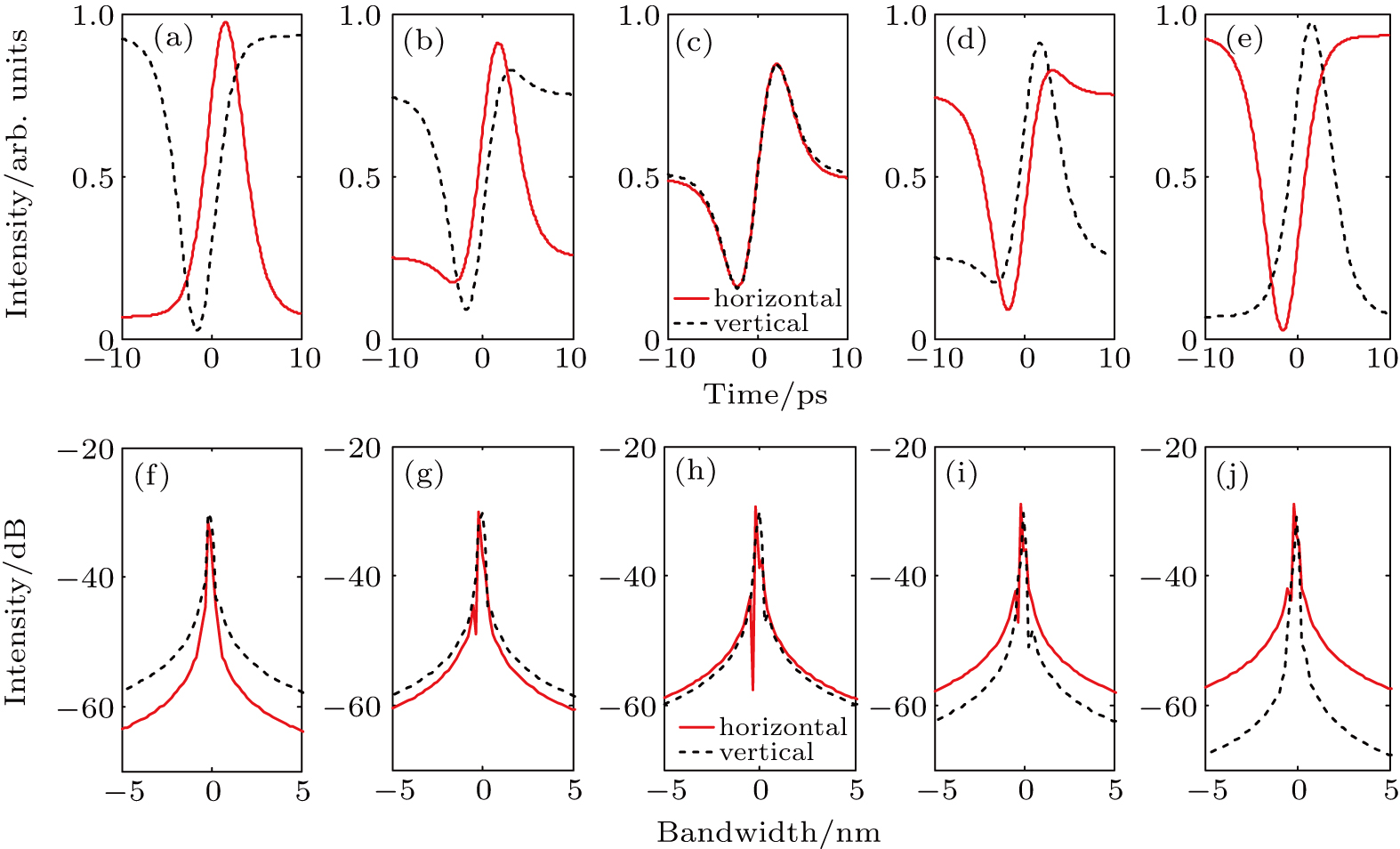
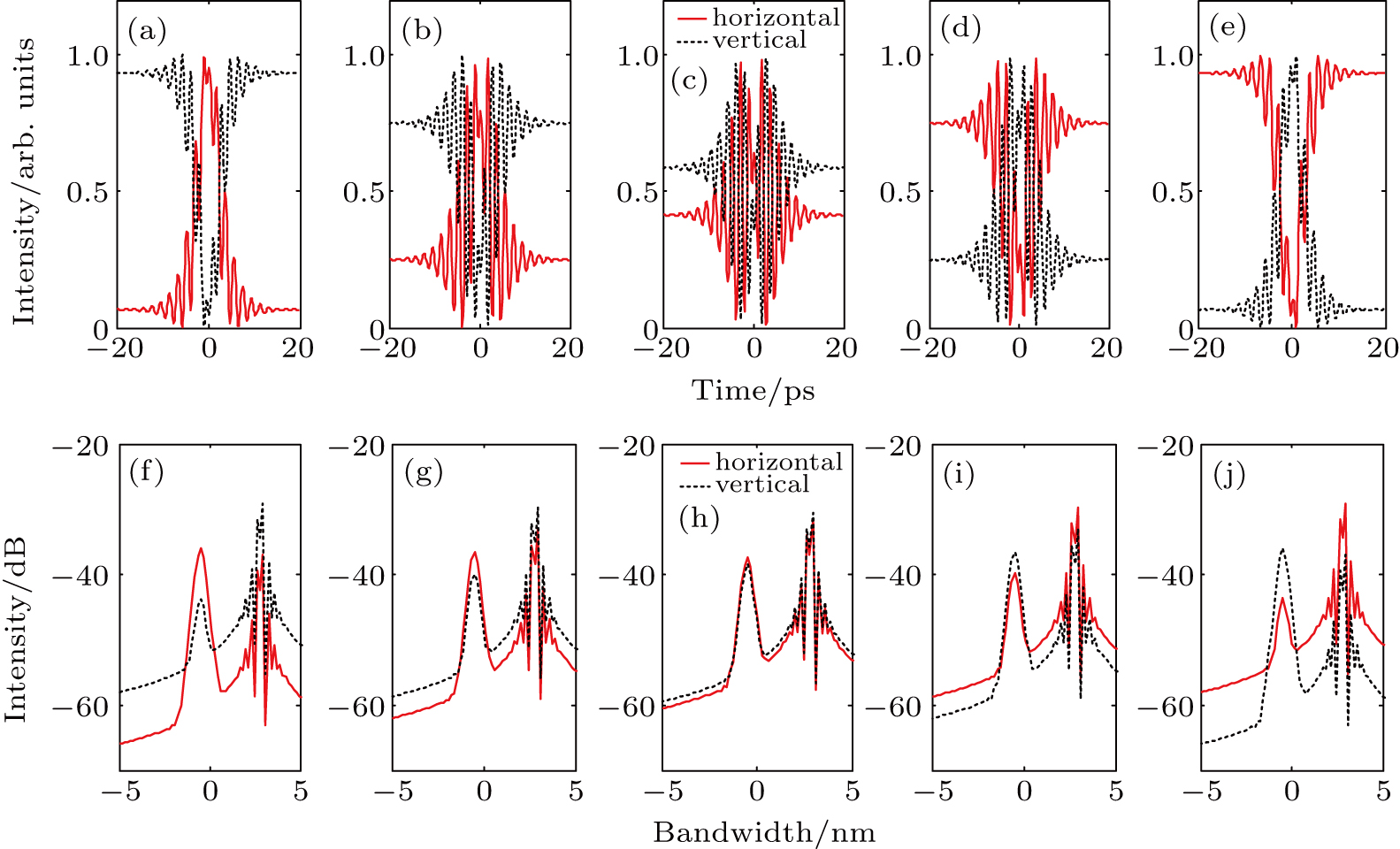
At last, we consider the influence of the phase difference Δφ on the output pulse properties. Figure
In this section, we simulate the output pulse shapes and optical spectra when λ1 ≠ λ2, which is the characteristic of GVLVS. Because for GVLVS, the two orthogonal polarization modes will shift their central wavelengths, combining with self-phase modulation (SPM) and XPM to compensate linear intra-cavity fiber birefringence. In later simulations, we set λ1 = 1063 nm and λ2 = 1065 nm, and the simulation procedure is similar to the former case when λ1 = λ2. Firstly, the amplitude ratio (A2/A1) of incident pulses is decreased from 3/1 to 1/3, and others are set as: θ = 0°, ΔT = 0 ps, and Δφ = 0. The simulation result is shown in Fig.
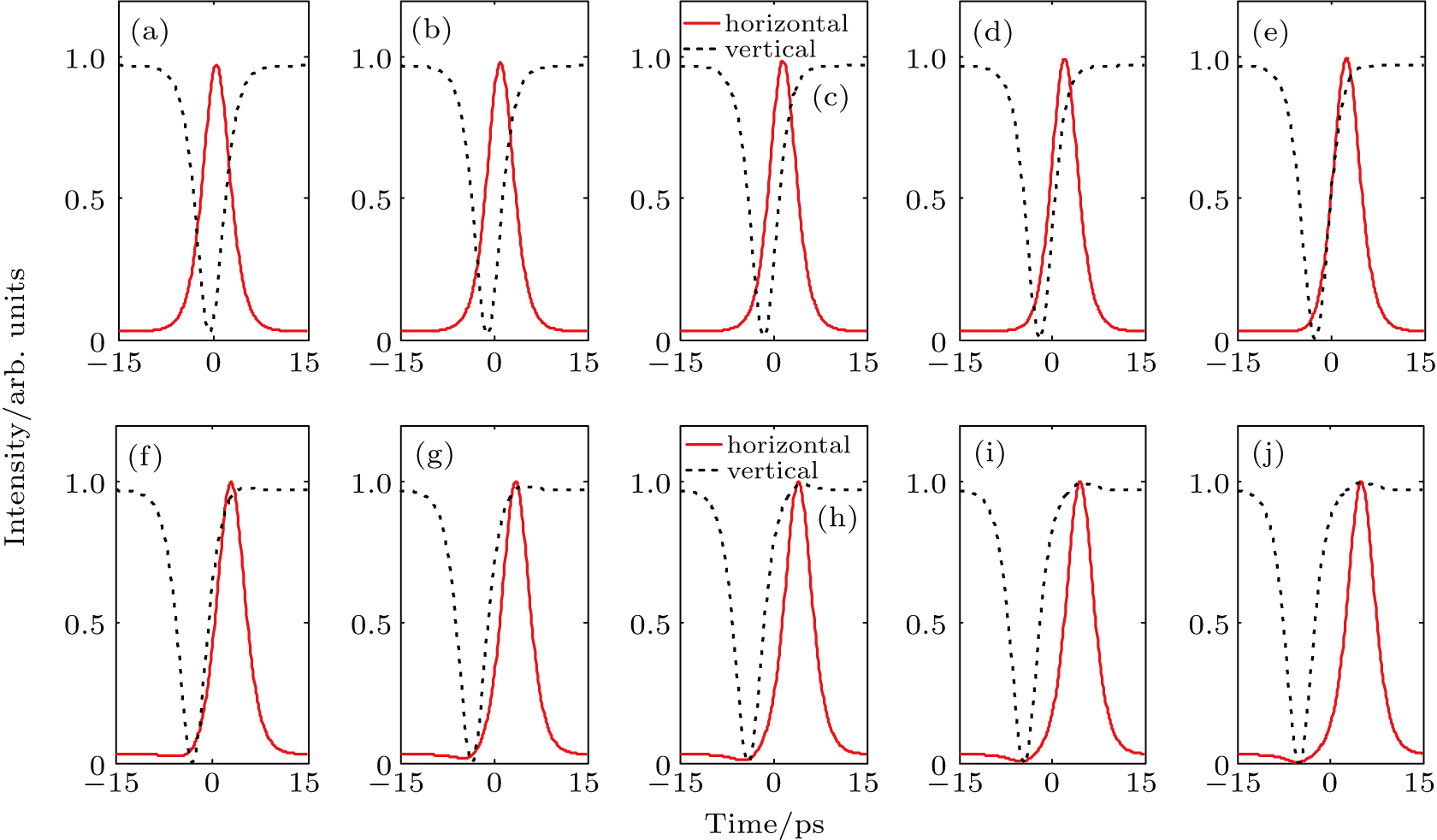
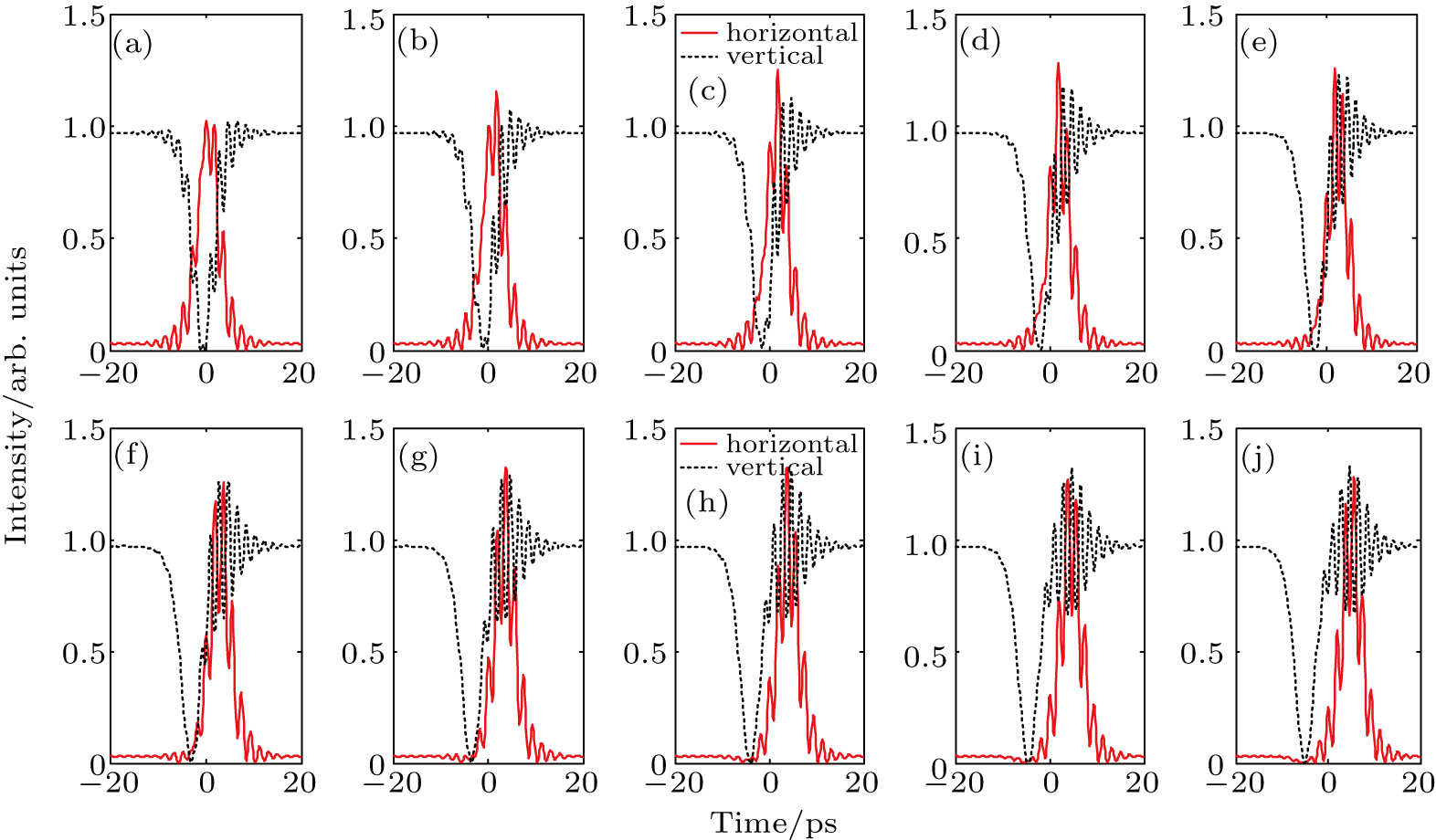
Then, we change projection angle θ and simulate the pulse shaping properties for incident group-velocity-locked bright–dark vector soliton pair. Figure
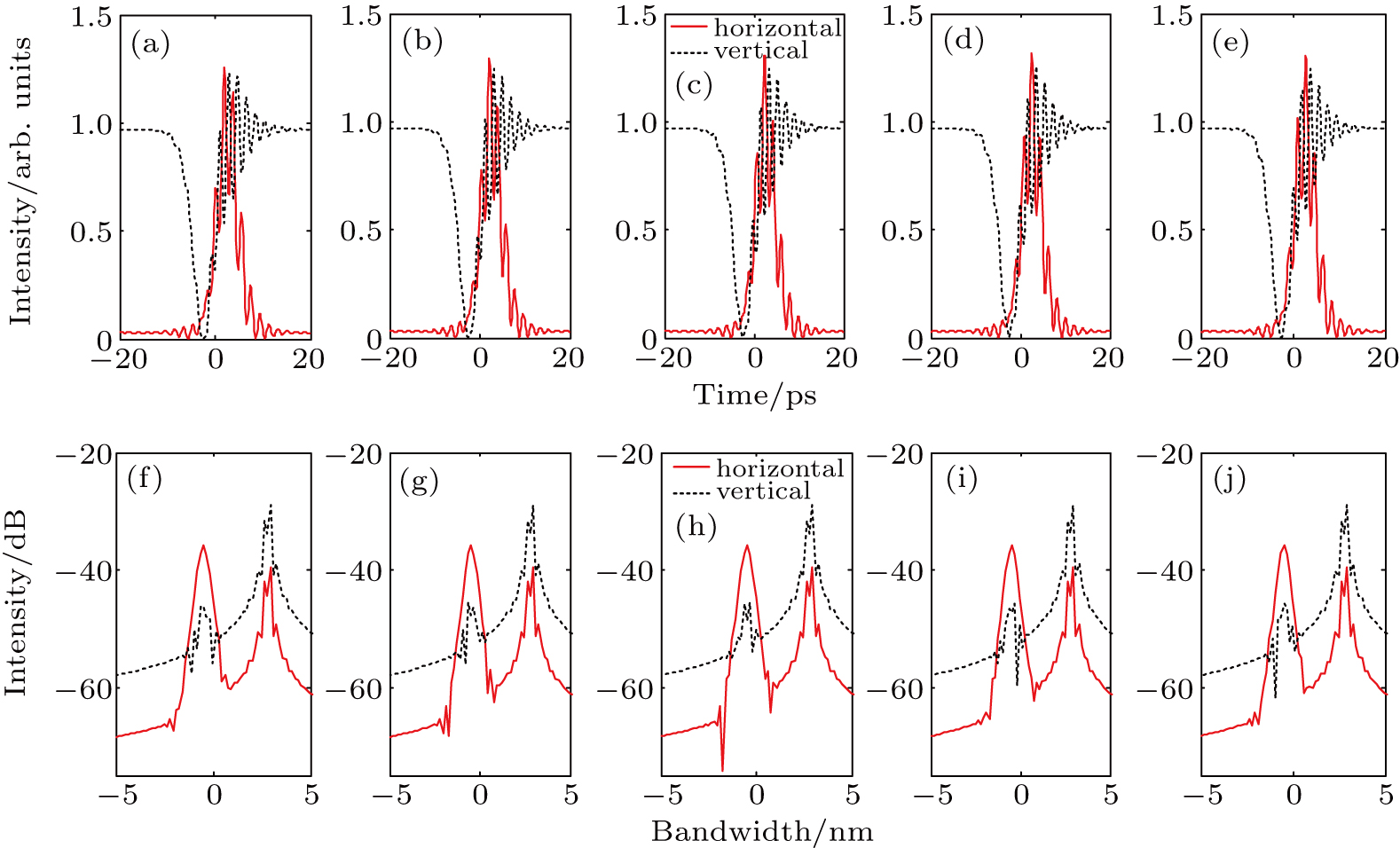
After that, the time delay ΔT is changed while with other variables fixed at appropriate values. ΔT increases from 1 ps to 10 ps while others are set as: A1 = A2 = 1, θ = 10°, and Δφ = 0. The simulation results are demonstrated in Fig.
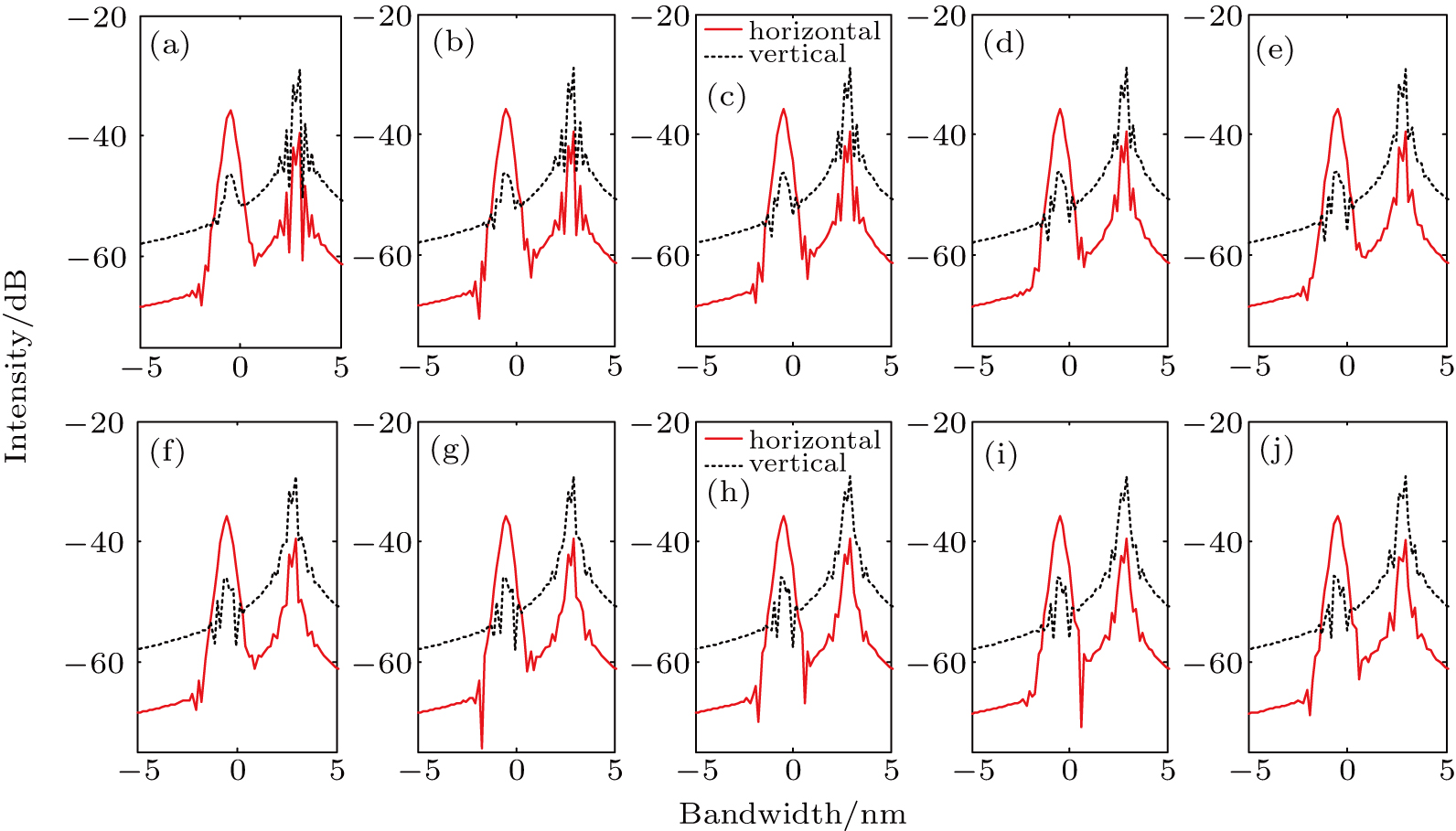 | Fig. 10. Simulated output optical spectra [(a)–(j)] in orthogonal polarization directions when time delay ΔT increases from 1 ps to 10 ps (1-ps time interval). Others are the same as those in Fig. |
At last, we simulate the pulse shaping through changing phase difference Δφ. Figure
It should be noted that the simulation results in Figs.
We simulated the pulse shaping of bright–dark vector soliton pair at 1-μm wavelength region. Through changing input pulse pair parameters, various kinds of pulse shapes and optical spectra can be generated. When the orthogonal modes have the same central wavelength, “2+2”- and “1+2”-type pseudo-high-order polarization-locked bright–dark vector soliton pairs can be generated. While for different central wavelengths, group-velocity-locked bright–dark vector soliton pairs with chirp-like oscillated pulses at pulse trailing edge position can be generated. Our simulations can provide beneficial conduct for experiments about pulse shaping of bright–dark vector soliton pair with different wavelengths.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |