Trajectory engineering via a space-fractional Schrödinger equation with dynamic linear index potential

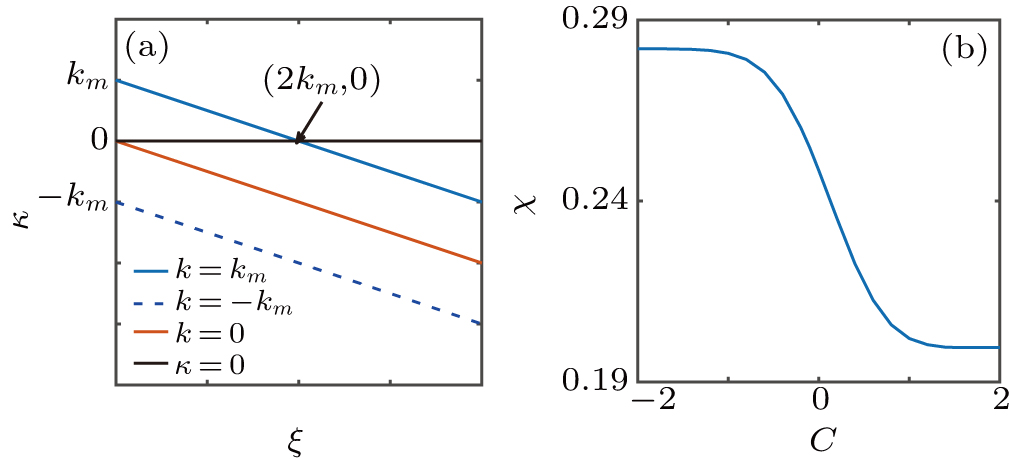
Meng Yunji^{1, †}, Liu Youwen², Lv Haijiang¹

(a) The trajectories of three different frequency components κ (k;ξ) = k – ξ/2. Solid blue: k = k_m (k_m is the maximum frequency component); dashed blue: k = –k_m; solid orange: k = 0. The horizontal line κ = 0 and line k = k_m intersect at the shift point (2k_m,0), after which κ(ξ) < 0 always holds. (b) Dependence of the integral form-factor on the linear chirp.