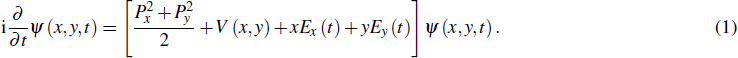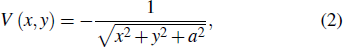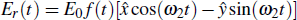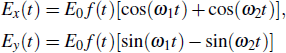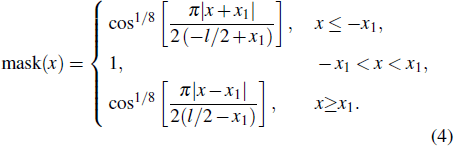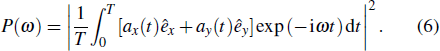1. IntroductionWith the rapid development of intense laser field, the progresses on the high-order harmonics generated from atoms,[1,2] molecules,[3] and solids[4,5] interacting with an intense laser field have been made. High-order harmonic generation (HHG) is a highly nonlinear process which can be used to obtain attosecond pulse in the XUV regime. It enables us to trace and probe the ultrafast processes of electrons in atoms and molecules[6] and control the electron dynamic processes.[7–11] The semi-classical three-step model can well explain the HHG mechanism.[12] Firstly, the electrons in atoms are ionized by the tunneling from ground state to continuous state. Then the electrons propagate in the laser field and gain the extra kinetic energy. Finally, the electrons recombine with the parent nuclei and release the high-energy photons when the laser direction is reversed. The harmonic spectrum has the typical characteristic, it contains a sharp decrease, nonperturbative plateau, and ends up with a cutoff at photon energy Ip + 3.17Up, where Ip is the ionization potential and Up is the ponderomotive energy.
In the past, many characteristics of the high order harmonics have been investigated widely. For instance, the initial coherent superposition state of the helium ion has been investigated to improve the efficiency of the high order harmonics.[13] How to obtain ultra-short attosecond pulse through the high order harmonics has become a hot topic, it is recognized that HHG is the most promising method to synthesize isolated attosecond pulse (IAP).[14,15] Recently, the linearly short single pulses with durations of 43 as (see Ref. [16]) and 53 as (see Ref. [17]) have been generated by atomic HHG, respectively. The high order harmonics generated by the interaction of a linearly polarized laser with atoms and molecules can be used to generate a linearly isolated attosecond pulse. However, the application of linearly polarized attosecond pulse is restricted to its inherent one dimensionality. Therefore, non-linearly polarized attosecond pulse has been widely investigated in recent years.[18–23]
A great deal of work has been done in the bichromatic counter-rotating circularly polarized (BCCP) driving laser field in previous years, which consists of two coplanar counter-rotating circularly polarized laser fields with different angular frequencies. The circularly polarized HHG spectra driven by BCCP laser field has a doublet structure, the helicity of the right peak in the doublet is the same as that of the higher frequency driving field, and the helicity of left peak is the same as the driving field with the lower frequency.[24] Medišauskas et al.[25] theoretically demonstrated that the highly ellipticity attosecond pulses can be generated at the single-atom level by using BCCP driving pulses. Recently, the properties of HHG driven by BCCP laser field have received extensive attention. Milošević summarized the general selection rules of high-order harmonic emission of atoms in BCCP driving laser field with frequencies of rω and sω (r and s are integers), and extended the rules to elliptically polarized laser field.[26] The polarized property of the high harmonics from N2 molecule is investigated in a BCCP laser field, the results show that the helicity of the harmonic is reversed at particular harmonic orders.[27]
In this paper, we investigate the properties of HHG in a BCCP driving laser field by numerically solving the two-dimensional (2D) time-dependent Schrödinger equation (TDSE) with a coulomb potential of argon atom. Our results show that the harmonic spectra of the odd-order harmonics, the even-order harmonics and the semi-integer-order harmonics can be generated by changing the wavelength of right-circularly polarized laser field. The generation of the semi-integer-order harmonics is explained by numerical statistics of the number of harmonic absorbed photons and the quantum transition theory, respectively. In this paper, the atomic units (a.u.) are used otherwise stated.
2. Theoretical modelWe have investigated the properties of HHG from an argon atom by numerically solving the 2D time-dependent Schrödinger equation. The 2D TDSE in the length gauge can be written as
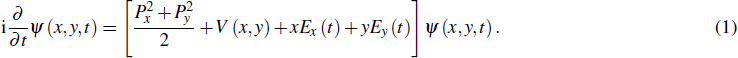
The 2D model potential of an argon atom is given by
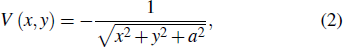
where
a = 0.62 is the soft-core parameter corresponding to the ionization potential of an argon atom (
Ip = 15.8 eV).
[28]
As we know, a bicircular polarized laser field is composed of a left-circularly polarized laser and a right-circularly polarized laser, the BCCP laser field is given by

where

is the left-circularly polarized laser field and
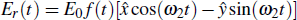
is the right-circularly polarized laser field.
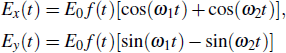
are the electric field along the
x and
y directions, respectively.
E0 is the amplitude of the laser field,
f(
t) is the trapezoidal envelope of the laser pulse with 2 cycles ramp on, 5 cycles plateau, and 2 cycles ramp off. The duration of the laser pulse
T is nine optical cycles. The
ω1 and
ω2 represent the angular frequencies of the left- and right-circularly polarized laser fields, respectively, and
ω2 =
γω1, where
γ is a real number. The wavelength of the left-circularly polarized laser field remains unchanged which is fixed at 800 nm (
ω1 = 0.056 a.u.), while the wavelength of the right-circularly polarized laser field is changed from 100 nm to 900 nm (
ω2 is from 0.448 a.u. to 0.049 a.u.). We use the method of the split-operator to solve the TDSE, and the space step is 0.4 a.u., the time step is ⧍
t = 0.15 a.u., and the spatial integration grid size is 409.6 a.u. In order to avoid the reflection of wave functions at the boundary, we set a ‘mask function’ with the following form:
[29]
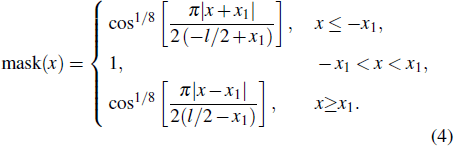
The dipole acceleration can be obtained by the Ehrenfest theorem
[30]

The HHG spectrum can be obtained by taking the modulus squared of the Fourier transformation of
a(
t),
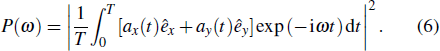
3. Results and discussionIn Fig. 1, we show the harmonics spectrum from an argon atom by the BCCP laser field with the laser peak intensity I0 = 1 × 1014 W/cm2 when the wavelength of the right-circularly polarized laser is varied from 100 nm to 900 nm (ω2 is from 0.448 a.u. to 0.049 a.u.), while the wavelength of the left-circularly polarized laser is fixed at 800 nm (ω1 = 0.056 a.u.).
From Fig. 1 we can see that the harmonics spectra vary drastically with the change of the right-circularly polarized laser wavelengths. When the wavelengths are selected as 800nm for both beams, the laser field becomes a linearly polarized field, only the odd-order harmonics can be generated as shown by the solid blue line in Fig. 1. When the wavelengths of left-circularly and right-circularly polarized laser are selected as 800 nm and 400 nm, respectively, the BCCP driving laser field with the angular frequencies (ω1 and ω2 = 2ω1) exhibits threefold spatiotemporal symmetry. In this case, the 3n-order harmonics are suppressed, only the (3n ± 1)-order harmonics can be generated, which is shown by the solid purple line in Fig. 1. These interesting results have been investigated both experimentally[31,32] and theoretically.[25,33]
As the wavelength of right-circularly polarized field decreases from 900 nm to 100 nm, the harmonics spectrum starts to get complicated. As can be seen from Fig. 1, the harmonics spectra are gradually splitting with the decrease of the right-circularly polarized laser wavelengths. The harmonic orders move towards the higher frequency which corresponds to the blue shift of the harmonics. While, the position of the first order harmonic remains unchanged. We can see that not only the integer-order harmonics can be generated, but the non-integer-order harmonics can also be generated, which includes the semi-integer-order harmonics generation. In our work, we only investigate the generation of the semi-integer-order harmonics. The four dotted red lines in Fig. 1 show that the semi-integer-order harmonics are generated when the wavelength of right-circularly polarized laser field is selected as 533nm, 320nm, 228nm, and 177nm, the angular frequency ratio of the corresponding right- and left- circularly polarized laser is γ = 1.5, γ = 2.5, γ = 3.5, and γ = 4.5, respectively.
To illustrate how the semi-integer-order harmonics are generated, we investigate the harmonics spectrum as shown in Fig. 2 with the right-circularly polarized laser wavelengths 533 nm, 320 nm, 228 nm, and 177 nm, which correspond to the frequency ratios γ = 1.5, 2.5, 3.5, 4.5 of the right- and left-circularly polarized laser pulse.
Figure 2(a) shows that the integer-order harmonics (the orders 1, 4, 6, 9, 11, etc.) and the semi-integer-order harmonics (the orders 1.5, 3.5, 6.5, 8.5, 11.5, etc.) can be generated with the frequency ratio γ = 1.5. Figure 2(b) shows that the integer-order harmonics (the orders 1, 6, 8, 13, 15, etc.) and the semi-integer-order harmonics (the orders 2.5, 4.5, 9.5, 11.5, 16.5, etc.) can be generated with the frequency ratio γ = 2.5. Figure 2(c) shows that the integer-order harmonics (the orders 1, 8, 10, 17, 19, etc.) and the semi-integer-order harmonics (the orders 3.5, 5.5, 12.5, 14.5, etc.) can be generated with the frequency ratio γ = 3.5. Figure 2(d) shows that the integer-order harmonics (the orders 1, 10, 12,etc.) and the semi-integer-order harmonics (the orders 4.5, 6.5, 15.5, 17.5, etc.) can be generated with the frequency ratio γ = 4.5. Therefore, the coupling between the two circularly polarized laser field with semi-integer frequency ratio can generate the semi-integer-order harmonics. The general for the possible harmonic order can be derived[26] q = p(γ + 1) ± 1, p is an integer. When γ is selected as a semi-integer, integer-order harmonics and the semi-integer-order harmonics can be generated. When γ is selected as the non-integer (excluding semi-integer), the other non-integer-order harmonics can also be generated according to the above rules as shown in Fig. 1. As the frequency ratio γ increases, when p is the same, the interval between adjacent orders of the emitted harmonics will become larger. This increasing interval will results in the spllited curve is not smooth and shows some hot spots as shown in Fig. 1. To illustrate the law of the processes of the HHG, we will give the explanation by the photon absorption rule.
To better illustrate the harmonics generation shown in Fig. 2, we summarize the rules of the number of photons absorbed for four types of harmonic orders which includes the integer-order, odd-order, even-order, and semi-integer-order as shown in Table 1. According to the Center symmetry and parity conservation, the harmonics can only be produced by absorbing an odd number of photons. The absorption and emission of photons can be used to explain the law of harmonic generation in BCCP laser field. Table 1 presents the generation of different types of the harmonic orders, ω1 represents the left-handed photon which is absorbed from left-circularly polarized laser field, ω2 (1.5ω1/2.5ω1/3.5ω1/4.5ω1) represents the right-handed photon which is absorbed from right-circularly polarized laser field.
Table 1.
Table 1.
 Table 1.
The rules of the number of photons absorbed for different types of harmonic orders. Where ω1 is the photons absorbed from left-circularly polarized laser field, ω2 is the photons absorbed from right-circularly polarized laser field, ω2 = γω1, γ = 1.5, 2.5, 3.5, 4.5. n and m are integers.
.
|
ω2 photons |
ω1 photons |
| (1.5ω1/2.5ω1/3.5ω1/4.5ω1) |
| Integer harmonics |
2n
|
2m + 1 |
| Odd harmonics |
4n
|
2m+1 |
| Even harmonics |
4n+2 |
2m+1 |
| Semi-integer harmonics |
2n+1 |
2m
|
| Table 1.
The rules of the number of photons absorbed for different types of harmonic orders. Where ω1 is the photons absorbed from left-circularly polarized laser field, ω2 is the photons absorbed from right-circularly polarized laser field, ω2 = γω1, γ = 1.5, 2.5, 3.5, 4.5. n and m are integers.
. |
From Table 1, it can be demonstrated that the harmonic emission needs to absorb (2m+1) left-handed photons and 2n right-handed photons to generate the integer-order harmonics. Among them, the absorption of (2m+1) left-handed photons and 4n right-handed photons produce the odd-order harmonics, while the absorption of (2m+1) left-handed photons and (4n+2) right-handed photons produce the even-order harmonics. It can also be demonstrated that the harmonic order emitted needs to absorb 2m left-handed photons and (2n+1) right-handed photons to generate the semi-integer-order harmonics.
When the frequency ratio of right- and left-circularly polarized laser is 1.5, the harmonic orders of 1, 1.5, 3.5, 4, 6, 6.5, 8.5, 9, etc. can be obtained as shown in Fig. 2(a). For the integer-order harmonics, the harmonic orders are in agreement with formula (2m+1) × ω1 + (2n) × 1.5 ω1. When m = 0 and n = 0, it absorbs one ω1 photon so that the 1-order harmonic can be emitted (1 × ω1 = ω1); When m = 0 and n = 1, it absorbs one ω1 photon and two ω2 = 1.5ω1 photons so that the 4-order harmonic can be emitted (1 × ω1 + 2 × 1.5 ω1 = 4ω1); When m = 1 and n = 1, it absorbs three ω1 photons and two ω2 = 1.5ω1 photons so that the 6-order harmonic can be emitted (3 × ω1 + 2 × 1.5 ω1 = 6ω1), and so on. For the semi-integer-order harmonics, the harmonic orders are in agreement with formula 2m × ω1 + (2n + 1) × 1.5 ω1. When m = 0 and n = 0, it absorbs one ω2 = 1.5ω1 photon so that the 1.5-order harmonic can be emitted (1 × 1.5 ω1 = 1.5ω1); When m = 1 and n = 0, it absorbs two ω1 photons and one ω2 = 1.5ω1 photon so that the 3.5-order harmonic can be emitted (2 × ω1 + 1 × 1.5ω1 = 3.5ω1); When m = 1 and n = 1, it absorbs two ω1 photons and three ω2 = 1.5ω1 photons so that the 6.5-order harmonic can be emitted (2 × ω1 + 3 × 1.5ω1 = 6.5ω1), and so on.
When the frequency ratio of right- and the left-circularly polarized laser is 2.5, the harmonic orders of 1, 2.5, 4.5, 6, 8, 9.5, 11.5, 13, etc. can be obtained as shown in Fig. 2(b). For the integer order harmonics, the harmonic orders are in agreement with formula (2m + 1) × ω1 + (2n) × 2.5 ω1. When m = 0 and n = 0, it absorbs one ω1 photon so that the 1-order can be emitted (1 × ω1 = ω1); When m = 0 and n = 1, it absorbs one ω1 photon and two ω2 = 2.5ω1 photons so that the 6-order can be emitted (1 × ω1 + 2 × 2.5ω1 = 6ω1); When m = 1 and n = 1, it absorbs three ω1 photons and two ω2 = 2.5ω1 photons so that the 8-order can be emitted (3 × ω1 + 2 × 2.5 ω1 = 8ω1), and so on. For the semi-integer-order harmonics, the harmonic orders are in agreement with formula (2m) × ω1 + (2n + 1) × 2.5ω1. When m = 0 and n = 0, it absorbs one ω2 = 2.5ω1 photon so that the 2.5-order can be emitted (1 × 2.5 ω1 = 2.5ω1); When m = 1 and n = 0, it absorbs two ω1 photons and one ω2 = 2.5ω1 photon so that the 4.5-order harmonic can be emitted (2 × ω1 + 1 × 2.5ω1 = 4.5ω1); When m = 1 and n = 1, it absorbs two ω1 photons and three ω2 = 2.5ω1 photons so that the 9.5-order harmonic can be emitted (2 × ω1 + 3 × 2.5 ω1 = 9.5 ω1), and so on. We can also investigate the harmonic orders when the frequency ratios are 3.5 and 4.5, which are also in good agreement with that shown in Figs. 2(c) and 2(d), respectively.
To clearly describe the photon absorption and emission rules tabulated in Table 1 and better illustrate the semi-integer-order harmonics generation shown in Fig. 2, we give the quantum transition diagram as shown in Fig. 3. The process of harmonic emission follows the energy conservation law and the angular momentum conservation. For the energy conservation, ωn = lω1 + kω2, where l is the number of photons absorbed from the left-circularly polarized laser field, k is the number of photons absorbed from the right-circularly polarized laser field and ωn is the energy of the HHG. The general selection rules of HHG in the elliptically polarized laser field with the photon frequencies of rω and sω are investigated in Ref. [26], where r and s are integers. In this view, the selection rules of integer-order harmonic generation are given. Different from the general for the possible harmonic order in bichromatic circularly polarized laser field given in Ref. [26] by using the dynamical symmetry, we investigate the mechanism of semi-integer order harmonic generation by analyzing the number of photons absorbed from the left- and right-circularly polarized laser fields. Furthermore, we study the rules of semi-integer-order harmonics generation according to energy conservation and parity conservation. In the case of semi-integer-order harmonics, l = 2m and k = 2n + 1 as shown in Table 1. According to the parity of forbidden, not all harmonics of order can be generated,[31,33] only the absorption of an odd number of photons can lead to the emission of the harmonics, the angular momentum is 1 or −1. Therefore, for the angular momentum conservation l = k ± 1.
The HHG in Fig. 3(a) is consistent with what has been shown in Fig. 2(a), where the law of photonic transition of 11.5-order and 13.5-order harmonic absorptions is illustrated as an example. As we can see, the harmonic of 11.5-order needs to absorb l = 4 left-handed photons and k = 5 right-handed photons ωn = 4 × ω1 + 5 × 1.5 ω1 = 11.5 ω1 and the harmonic of 13.5-order needs to absorb l = 6 left-hand photons and k = 5 right-handed photons ωn = 6 × ω1 + 5 × 1.5ω1 = 13.5ω1. These results show that only by absorbing one more left-handed or right-handed photons can cause the emission of the harmonics. Therefore, 11.5-order and 13.5-order harmonics can be generated.