† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 21674078, 21474074, 21574096, 21774091, and 21374073) and Overseas Research Program of Jiangsu, China (2019).
Computer simulations were performed to study the dense mixtures of passive particles and active particles in two dimensions. Two systems with different kinds of passive particles (e.g., spherical particles and rod-like particles) were considered. At small active forces, the high-density and low-density regions emerge in both systems, indicating a phase separation. At higher active forces, the systems return to a homogeneous state with large fluctuation of particle area in contrast with the thermo-equilibrium state. Structurally, the rod-like particles accumulate loosely due to the shape anisotropy compared with the spherical particles at the high-density region. Moreover, there exists a positive correlation between Voronoi area and velocity of the particles. Additionally, a small number of active particles capably give rise to super-diffusion of passive particles in both systems when the self-propelled force is turned on.
Active matter refers to a variety of systems ranging from schools of fish on a macroscale to swarms of bacteria on a microscopic scale.[1] The common feature of these systems is that the constituents locally convert energy into motion. At a high density of constituent units, these systems can be viewed as a living material with the ability to adapt to stimuli, heal itself, like a biological tissue.[2] The far-from-equilibrium feature of these systems leads to rich phenomena such as giant fluctuation,[3–5] phase separation,[6] and super-diffusion.[7–9]
It was shown that active systems consisting of self-propelled particles interacting solely via repulsive interaction phase separate into a solid-like phase and a gas-like phase at very low area fractions in two dimensions.[10] This motility induced phase separation (MIPS) has been observed in many simulations of self-propelled particles[11,12] and also realized experimentally in a system of colloids.[13] However, it is very challenging to reach a high packing fraction in experiments of pure self-propelled particles to investigate the phase-separation behaviors. Most experiments have been carried out with highly diluted suspension of self-propelled particles.[14] Thus, numerical experiments were performed to study the complex phase behavior of dense self-propelled systems.
Recently, the mixtures of self-propelled particles (SPPs) and passive particles or chains in two dimensions have been intensively studied.[15–17] The mixtures provide an additional degree of control for performing specific functions. For example, self-propelled particles lead to the globule–stretch transition of a self-attracting chain due to shear-induced stretching at a low rotational diffusion of SPPs or collision-induced melting at a high rate of SPPs.[18] The mixtures of monodisperse repulsive active Brownian particles and their passive counterparts also display a MIPS behavior, similar to the monodisperse active system, except the existence of enhanced fluctuations and frequent fission and fusion of clusters.[19] The big passive athermal particles display an effective attraction in the bath of small SPPs, which leads to a true phase separation for large size rations and area fraction of SPPs.[17] Recent experiments and simulations also focused on the passive tracers with various shapes such as ellipsoid,[20] chevrons,[21] and wedge[22] in the active suspensions, and found the existence of enhanced diffusion in the translational and rotational degrees. Although there are lots of works on monodisperse SPPs and mixtures of spherical passive particles and SPPs at high area fractions,[15,19,23–25] the mixture of rod-like particles and SPPs has not been investigated so far.[26]
In this paper, we computationally study a binary active mixture of rod-like particles and SPPs with total area fraction φ0 = 0.6, using the active Brownian particle model. Here we focus on the low ratio of SPPs with the area fraction φa ∼ 0.015 (i.e., the area fraction of the passive particles is 0.585), which is easy to be realized in colloidal systems.[27] Meanwhile, we also study the mixture of monodisperse SPPs and passive particles with the same fraction and the same ratio of SPPs. We address the following questions. What is the effect of the self-propelled force on the structure and dynamics of the two systems? And what is the structural difference between the two systems? We find both systems exhibit phase separation and super-diffusion as the self-propelled force is turned on, and the phase separation disappears at a large self-propelled force. Structurally, the rod-like particles accumulate loosely compared with the spherical particles at high-density regions due to the shape anisotropy.
The structure of this paper is as follows. We first outline our model and computational methods for both binary-mixture systems. Then, we describe our results and give necessary discussion. Finally, we provide the conclusion and outlook.
Our dimer system consists of a binary mixture of Nr rod-like particles (or Np = 2Nr passive beads for the monomer system) and Na SPPs moving on a two-dimensional frictional substrate (Fig. 
To mimic the passive rod-like particles, two beads are connected by a stiff harmonic spring via a harmonic potential 
The motion of each bead with constant mass m is governed by Newton’s equation[29]


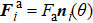
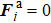

The pairwise interaction 

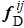



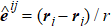
The pair interaction between any two beads in the system is modeled with a purely repulsive Weeks–Chandler–Andersen (WCA) potential

All simulations have been performed in a square box of size 100σ × 100σ with periodic boundary conditions using the home-modified LAMMPS software.[31] The dimer system consists of Nr = 3700 rod-like particles and Na = 200 SPPs. The monomer system consists of Np = 7400 passive beads and Na = 200 SPPs, insuring that the area fraction of the active particles is φa ∼ 0.015. We use m, σ, and kBT as the fundamental units for mass, length, and thermal energy, respectively. The simulations parameters are chosen as m = 1, σ = 1, kBT = 1, γdpd = 5.0, and Dr = 10–3. We set γS = 0.1 for Fa ≠ 0. But we technically set γS = 0 when the active force is turned off with the aim of getting enough samples of typical structures. The dimensionless time unit is 
Figure
There are three mechanisms of phase separation in binary mixture systems with purely repulsive interaction. One is the depletion-induced phase separation. The depletion effect induces an attractive force between large particles in the mixture because of the unbalanced osmotic pressure exerted on them by the surrounding small particles.[17] Active particles can also induce effective attraction between large passive colloidal particles, known as the active depletion.[33] Under these conditions, the range and strength of the effective attraction are crucially dependent on the shape and size of the passive particle. It was also found that the eccentric active particles can push passive spheres to form a large dense dynamic cluster, and the mixture of the passive spheres and eccentric active particles undergoes a dynamic de-mixing transition due to the entropy-driven depletion.[34] The second one is the diffusivity-induced phase separation in binary mixtures of monodisperse particles. An effective attractive interaction between the low diffusive particles results from the cage-effect by the surrounding high diffusive particles.[35] The third one is the motility-induced phase separation[36] and active–passive segregation.[19] The active–passive mixture shows enhanced fluctuations, with frequent fission and fusion of clusters. The clusters are not homogeneous, but are predominantly active at the periphery and passive in their interior. Our mechanism is similar to the MIPS, which is critically dependent on Péclet number (Pe) of the active particles. Here 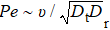


To qualitatively compare the structures of the two systems with the increase in self-propelled force, we first calculate the Voronoi area, S, of each bead (here we use “bead” to distinguish “particle”, because a rod-like particle consists of two beads). Figure
 | Fig. 3. (a) The deviation of Voronoi area as a function of Fa. The average Voronoi area of (b) passive beads and (c) active particles as a function of Fa for both systems. |
The average area of the passive beads increases with the increase in active force, while that of the active particles decreases with the increase in active force (Figs.
To get the quantitative difference of the structure of the binary mixture, we calculate the pair correlation functions (PCFs), g(r), between the particle pairs. It is a measure of the probability of finding a bead around the reference one. We present the PCFs between passive particles in Fig.
 | Fig. 4. The PCF of passive particles for (a) the monomer system and (b) the dimer system. (c) The PCF of active particles for both systems at various Fa. |
To further clarify the difference between the two systems, we also present g(r) of active particles in both systems for various active forces in Fig.
To study the correlation between velocity and area of the particles, we give the joint probability of velocity and Voronoi area of the active particles in Fig.
 | Fig. 5. The joint probability of velocity and Voronoi area of active particle for monomer (a) and dimer (b) systems at Fa = 1.0 (left), 5.0 (middle), 20.0 (right). |
To obtain the influence of SPP on the dynamics of the passive particles, we measure the mean square displacements (MSD) of the passive particles, 〈(r(t))2〉 = 〈(r(t) – r(0))2〉, at various Fa for both systems. We also calculate the scaling exponent β(t) = d[log(〈(Δr(t))2〉)]/d[log(t)] varying with time, as shown in Fig.
The study of how SPPs behave in crowded environments resembles realistic situations under which SPPs may be employed, e.g., as drug delivery systems. We performed molecular dynamics simulations with DPD thermostat to study two kinds of binary-mixtures in two dimensions: one is the mixture of passive and self-propelled spheres, the other is the mixture of rod-like particles and self-propelled spheres. Our results show that a very small number of active particles strongly influence the distribution and the dynamics of the dense mixtures. We find that, at a small active force, the high-density and low-density regions appear in both systems, indicating an emergence of phase separation. Then it vanishes at higher active forces due to the velocity improvement induced by frequent collision. Structurally, the rod-like particles accumulate loosely due to the shape anisotropy, compared with the spherical particles at the high-density region. In addition, we find the existence of positive correlation between Voronoi area and velocity of particles in both systems. Moreover, the passive particles show a super-diffusive behavior when the self-propelled force is turned on in spite of the low fraction of the active particles.
Here, we focus only on the dense systems with a low fraction of SPPs. In the future, the fraction effect of SPPs will be studied and the phase diagram might be given for the rod-like particle system.[38] Besides, the length of the rod-like particles is another interesting parameter that should be studied in further work.[39]
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |




