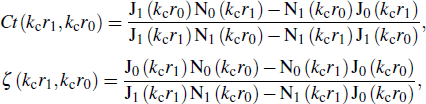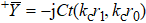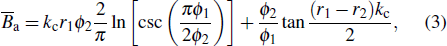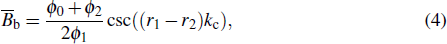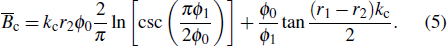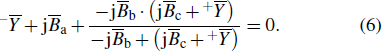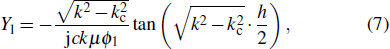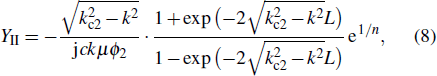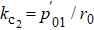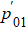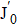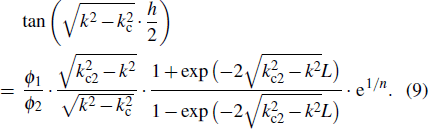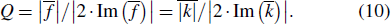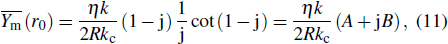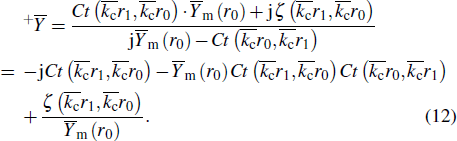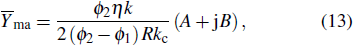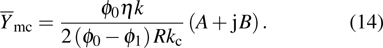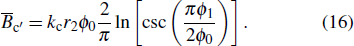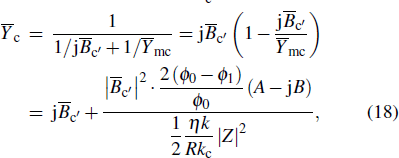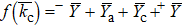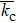1. IntroductionRecently, there was an increasing interest in radically-miniaturized masers such as compact rubidium masers (CRM) and passive hydrogen masers (PHM), which are used as atomic clocks in communication and localization applications.[1–9] Iris-loaded resonance cavity (IRC) is widely used in these masers. Compared with cylindrical cavity and sapphire-loaded cylindrical cavity, the IRC can greatly reduce the radial size of atomic clock.[10–14] In addition, its excellent mechanical property makes it suitable for aerospace and mobile applications. Besides, the IRC has a broad field of applications in electron spin resonance (ESR), electron paramagnetic resonance (EPR), and nuclear magnetic resonance (NMR), where it is named split-ring or slotted-tube resonator.[6]
However, the structure of the IRC is very complex and thus it is difficult to analyze. At present, some electromagnetic simulation softwares are used to obtain the key parameters of IRC, such as resonance frequency, quality factor, and magnetic energy filling factor. Unfortunately, such an approach is time- and memory-consuming, and also difficult to understandits physical mechanism.[14] Its electromagnetic parameters are calculated by using a lumped-element circuit model and some simple formulas are obtained, but their accuracy is larger than 10% and does not satisfy actual requirement.
In this paper, a theoretical model based on electromagnetic field theory is set up to analyze the IRC. The formulas to calculate key electromagnetic parameters of the IRC are presented, such as resonance frequency, quality factor, and magnetic energy filling factor. Because electromagnetic wave concept is introduced into the analysis model, the physical mechanism is clearly expounded and the formulas to calculate key parameters are accurate enough for actual cavity design. Finally, the model and formulas are verified by both electromagnetic (EM) simulations and experimental results. Compared with sole EM simulation approach, the method proposed in this paper is fast as well as accurate.
2. Transmission-line model of IRCThe structures of the IRC for the CRM and the PHM are shown in Figs. 1(a) and 1(b), respectively. The former is a cylindrical cavity with some irises connected to the wall by straight fins. There are two lids at the ends of the cylindrical cavity, which are not shown in this figure for simplicity. The IRC for the PHM shown in Fig. 1(b) is almost similar to that in Fig. 1(a) except the circular fins. Both of the cavities consist of four outer cavities, one inner cavity and two end gaps. The outer cavity and inner cavity are coupled through the end gaps and the slots between the irises. The irises are capacitively-loaded electrodes used for reducing the resonance frequency. So the volume of the cylindrical cavity could be reduced meanwhile the resonance frequency is kept constant (for the resonance frequency of rubidium maser 6.834 GHz and the resonance frequency of hydrogen maser 1.420 GHz). The metal fins are used to connect irises to the cavity wall for mechanical consideration. A thin-wall quartz cell is located in the inner cavity to store the active material (rubidium or hydrogen).
The IRC is a half-wavelength, open-circuited waveguide resonance cavity with a special cross-section shape.[16–19] The cavity operates at TE01δ mode. If the cutoff wave number of the TE01 mode in the cross-section is determined, the properties of the IRC can be determined easily. The cutoff wave number kc of this waveguide with a special cross-section shape can be obtained by the transverse resonance technique.[20] It is based on the fact that the field forms a standing wave in the transverse plane of the waveguide under the cutoff condition. In this case, the waveguide can be regarded as a resonant radial transmission line with an infinite axial length. The irises are capacitive-loaded discontinuities in the radial direction.
Due to the fact that the cavity structure is symmetric, we only consider a sector of the cross-section of the IRCs in the following analysis, and the results are shown in Fig. 1. For example, one sector of the IRC for the CRM is shown in Fig. 2(a). The angle of the iris is expressed as ϕ1 = ((r1 + r2)/2)/d approximately, where d is the slot length between the irises. In Fig. 2(b), one sector of the IRC for the PHM is shown. For simplicity, its semi-circular region is replaced by the region depicted by the dashed line in Fig. 2(b). Both the semi-circular region and the one depicted by the dashed line in Fig. 2(b) have the same area and thus their electromagnetic energy storage is almost equal in both cases. Therefore, the analysis model of the IRC for the PHM in Fig. 1(b) is the same as that in Fig. 2(a). In the following, weanalyze only the IRC for the CRM and the IRC for the PHM.
The structure in Fig. 2(a) can be treated as an iris loaded wedge-shaped radial resonant transmission line. The wave in this transmission line is in the TE-like mode. There are three important electromagnetic parameters in the design of the IRC, i.e., resonance frequency, quality factor, and magnetic energy filling factor. In order to sustain the microwave field applied to the maser, the resonance frequency of the IRC should be consistent with the operating frequency of the maser. In addition, the properly chosen quality factor of the microwave cavity should guarantee a low power loss and the starting of oscillation. Finally, the homogeneity of the magnetic field inside the IRC in terms of intensity and orientation is crucial to the performance of the maser and it is represented by the magnetic energy filling factor. In the following, how to calculate these parameters will be discussed in detail.
2.1. Resonance frequencyThe wedged shape radial transmission line shown in Fig. 2(a) can be transformed into a parallel planar transmission line by implementing the conformal transformation as shown in Fig. 3. The admittance of the transmission lines and the equivalent circuit parameters of the iris are also shown in this figure. A reference plane is chosen at left side of iris.  is the admittance seen into the left of the reference plane and
is the admittance seen into the left of the reference plane and  is the admittance seen into the right.
is the admittance seen into the right.  ,
,  , and
, and  represent the equivalent circuit parameters of the iris.
represent the equivalent circuit parameters of the iris.
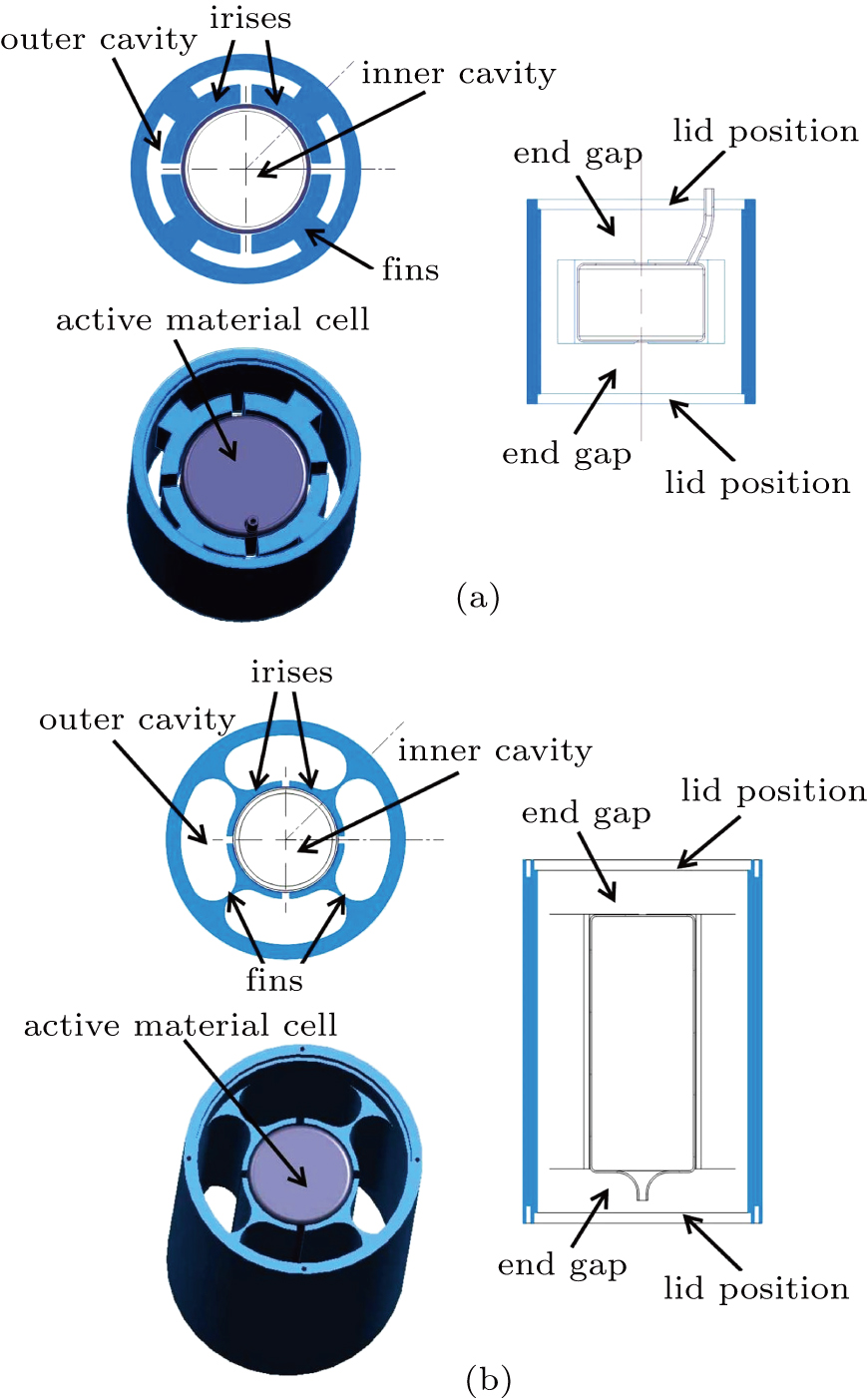
For the TE-like mode, the admittance of the radial transmission line can be written in the following form:[20]


where
J
0 and J
1 are the first kind of Bessel function. N
0 and N
1 are the second kind of Bessel function. At the surface of the outside cavity,

, so
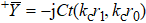
.
The equivalent circuit parameters of the iris in Fig. 3 are determined by the following equations:
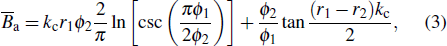
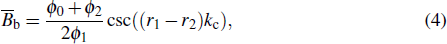
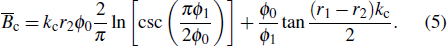
At any reference plane on the resonant transmission line, the sum of the input admittance seen looking into either side of the reference plane must be zero when the cavity is at a resonance state.
[19] So the following condition must be satisfied,
i.e.,
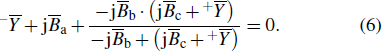
Then,
kc can be obtained by solving this equation.
The end gap between the irises and the lid should be included in the resonance frequency calculation. Here, half of the iris-loaded resonance cavity in Fig. 1 is considered due to its symmetry along the axis direction. The analysis model is presented in Fig. 4, where L is the length of the end gap and h is the length of the iris.
The wave admittance on the left-hand side of the interface is as follows:
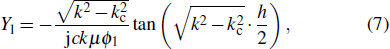
where
k is the free space wave number of the resonance frequency,
c is the light speed in vacuum, and
μ is the vacuum permeability.
The wave admittance on the right-hand side of the interface is
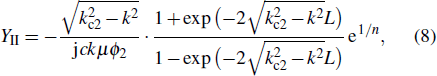
where
kc2 is the cutoff wave number of the TE
01 mode in a cylindrical waveguide.
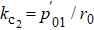
where
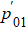
is the first root of the function
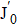
(
kc r0) = 0. Owing to the high-order modes excited by the end of the irises, a modification factor e
1/n related to the iris number
n should be added into the expression. Because the resonance frequency of the IRC is lower than the cutoff frequency of the TE
01 mode in cylindrical waveguide, the electromagnetic wave in the end gap is an evanescent wave and the propagation factor is an imaginary value.
[21–23]At resonance state, the wave admittance must be matched at the interface. Thus, we can obtain
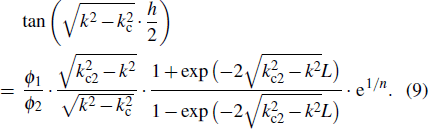
The free space wave number
k is obtained by solving this equation. The resonance frequency
f is determined by
f =
ck/(2
π).
2.2. Quality factorDue to finite conductivity of the cavity metal wall, the resonance frequency f, the free space wave number k and the cutoff wave number kc will be complex, and then be denoted as  ,
,  , and
, and  respectively. The quality factor of the cavity can be obtained through the following formula:[19]
respectively. The quality factor of the cavity can be obtained through the following formula:[19]
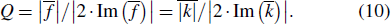
Let  , where kcr is the real part and kci the imaginary part. Due to kci ≪ kcr ≈ kc, the complex free space wave number
, where kcr is the real part and kci the imaginary part. Due to kci ≪ kcr ≈ kc, the complex free space wave number  can be calculated from Eq. (9) if the imaginary part of
can be calculated from Eq. (9) if the imaginary part of  , i.e., kci is known.
, i.e., kci is known.
On the inner surface of the outer cavity, r = r0, owing to the lossy metal wall, the surface admittance is[24]
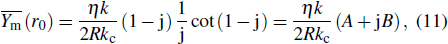
where
A = 0.6505,
B = −1.0856,
η is the wave impedance of vacuum,
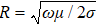
is the resistance of the cavity wall, and
σ is the resistivity of the cavity material.
At the iris position, i.e., r = r1, the admittance in Eq. (11) is transformed into
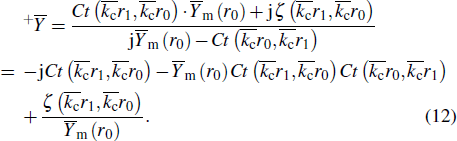
Similarly, the surface admittance on the left- and right-hand side of the iris are presented below:
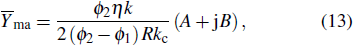
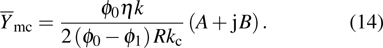
Assuming that they are independent of the surface admittance and the thickness of the iris is neglected, the shunting capacitive elements of the iris are simplified into

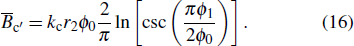
Thus, the total admittance on the iris is

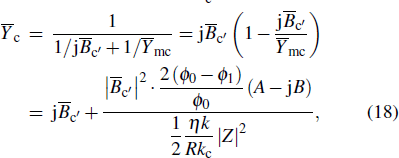
where |
Z|
2 = |
A|
2 + |
B|
2.
Regardless of the thickness of the iris, equation (6) is rewritten as

Given
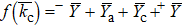
, we obtain

Then, we can obtain the imaginary part of the cutoff wave number from Eq. (20). Through some tedious manipulations, the imaginary part of  can be written as
can be written as

where

When the loss on the side wall of the outer cavity is taken into account, a factor
kci2 should be added into the imaginary part of
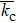
,
[25] and the resulting expression is as follows:

Since only the evanescent wave exists in the end gap, the loss in the end gaps is very small. It could be neglected in the quality factor calculation.
2.3. Magnetic energy filling factorThe magnetic energy filling factor measures the fraction of magnetic field energy useful for the clock signal with respect to the total microwave energy stored in the cavity. It is a measure of the efficiency of the cavity for coupling the overall microwave energy to the atoms stored in the cell, which is an important parameter for the maser, and this parameter is defined as[1]

where
Vb and
Vc are the volume of the active material cell and the volume of the total cavity, respectively. and
H and
Hz are the magnetic field and its axial component, respectively.
Because the field distribution is very complex in the cavity, it is difficult to obtain the value of the magnetic energy filling factor precisely. However, since magnetic field is distributed mainly along the axial direction, integrating the Hz field in the cell of active material and all cavities will yield an approximate expression of the magnetic energy filling factor as follows:

where
Vcell is the volume of the active material cell,
Vin and
Vout are the volume of the inner and outer cavity, respectively.
3. Simulated and measured resultsTo verify the validity of the above analysis, an IRC example for the miniaturized PHM is presented, whose structural parameters are listed in Table 1. The electromagnetic characteristics of this IRC example are investigated by both the transmission-line model in the previous section and the EM simulation based on finite element method (FEM).[26] Here the eigenmode of HFSS is used to calculate the property of the IRC.
Table 1.
Table 1.
 Table 1. Structural parameters of the IRC. .
| Parameter |
Value |
| r0/mm |
60 |
| r1/mm |
34 |
| r2/mm |
31 |
| d/mm |
4.8 |
| h/mm |
145 |
| L/mm |
20 |
| ϕ0 |
0.2136π |
| ϕ2 |
0.25 π |
| Cavity material |
aluminum |
| Surface roughness |
0.4 μm |
| Table 1. Structural parameters of the IRC. . |
Figure 5 shows the calculated and simulated variation of resonant frequency versus the iris gap length. The calculated results agree well with those obtained by the EM simulation and the difference is less than 0.5%, which verifies the validity of the transmission-line model in this paper. As can be seen from Fig. 5, the resonance frequency can decrease as the length d of the iris gap decreases. Therefore, we can reduce the cavity size by reducing the iris gap while the resonance frequency remains unchanged.
Figure 6 shows the calculated and simulated variation of frequency versus end gap length L. Because the inner cavity and outer cavity are coupled through the magnetic line in the end gap, the decrease of the end gap length will increase the resonance frequency. In practice, it is convenient to adjust the resonance frequency by changing the end gap length.
Figure 7 shows the calculated and simulated variation of quality factor versus iris gap length. The decrease of the iris gap will result in low quality factor of the cavity. So there is a tradeoff between the cavity size and the quality factor in the cavity design process. Because the loss at the end gap is omitted in the calculation, the calculated quality factor is larger than the EM one. However, the difference between them is less than 5% and it is good enough for actual design.
Figure 8 shows the calculated and simulated variation of magnetic energy filling factor versus iris radial location. By reducing the iris radial location, the magnetic energy filling factor slowly decreases. Figure 9 illustrates the magnetic field in one quarter of the PHM cavity. It shows that the magnetic field is distributed mainly along the axial direction, as assumed in the analytic model. The calculated results agree well with the simulated ones.
Finally, a prototype IRC for the PHM is fabricated to verify the theoretical model in this paper as shown in Fig. 10. The structure parameters are the same as listed in Table 1 except the roughness of the cavity surface which is about 1 μm. A silver film is coated on the cavity surface by electroplating technique to increase the conductivity and the quality factor. In Table 2, the calculated, simulated, and measured results of the IRC for the PHM are compared with each other. They accord well with each other, which verifies the analysis in this paper.
Table 2.
Table 2.
 Table 2. Calculated, simulated, and measured parameters of the PHM IRC. .
| Parameter |
Calculated |
EM simulated |
Measured |
| Resonance frequency |
1.474 GHz |
1.485 GHz |
1.480 GHz |
| Quality factor |
1.70 × 104 |
1.65 × 104 |
1.00 × 104 |
|
|
|
(loaded Q factor, S12 = 20 dB) |
| Table 2. Calculated, simulated, and measured parameters of the PHM IRC. . |