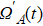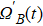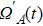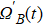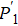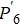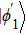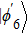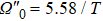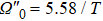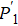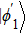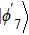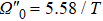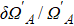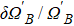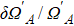Cite this Article
Tian Liang, Sun Li-Li, Zhu Xiao-Yu, Song Xue-Ke, Yan Lei-Lei, Liang Er-Jun, Su Shi-Lei, Feng Mang. Fast achievement of quantum state transfer and distributed quantum entanglement by dressed states. Chinese Physics B, 2020, 29(5): 050306  
Permissions
Fast achievement of quantum state transfer and distributed quantum entanglement by dressed states
Tian Liang1, Sun Li-Li2, Zhu Xiao-Yu1, 3, Song Xue-Ke4, Yan Lei-Lei1, Liang Er-Jun1, Su Shi-Lei1, †, Feng Mang1, 5
School of Physics, Zhengzhou University, Zhengzhou 450001, China
College of Physics, Tonghua Normal University, Tonghua 134000, China
College of Science, Henan University of Engineering, Zhengzhou 451191, China
School of Physics and Material Science, Anhui University, Hefei 230601, China
State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China

 

† Corresponding author. E-mail: slsu@zzu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11804308).

Abstract

We propose schemes to realize quantum state transfer and prepare quantum entanglement in coupled cavity and cavity–fiber–cavity systems, respectively, by using the dressed state method. We first give the expression of pulses shape by using dressed states and then find a group of Gaussian pulses that are easy to realize in experiment to replace the ideal pulses by curve fitting. We also study the influence of some parameters fluctuation, atomic spontaneous emission, and photon leakage on fidelity. The results show that our schemes have good robustness. Because the atoms are trapped in different cavities, it is easy to perform different operations on different atoms. The proposed schemes have the potential applications in dressed states for distributed quantum information processing tasks.

PACS: ;03.65.-w;;03.67.-a;
Keyword:;quantum state transfer;;dressed state method;;distributed quantum information processing;
1. Introduction

Quantum state transfer, to transfer the state of one atom to another one, is realized in many systems such as quantum spin networks system,[1] resonant cavity system,[2] disordered channels system,[3] spin chains system,[4] coupled-cavity arrays system.[5] In addition, a scheme is also proposed to improve the quantum state transfer by quantum partially collapsing measurements.[6] Quantum entanglement, an interesting and important phenomenon in quantum mechanics, is an important resource of quantum information processing,[7] such as quantum teleportation,[8,9] quantum secret sharing and secret splitting,[10] location-dependent communications,[11] quantum communication network,[12] and so on. Lately, the preparation of quantum entanglement is becoming more and more important and has been widely studied in cavity QED systems,[13–19] spin ensembles system,[20] multidimensional engineering system,[21] solid-state spin system,[22] nitrogen-vacancy centers system,[23] a quantum router,[24] (in a quantum router, an error-detected method has been proposed[25]) and so on. In addition, entangled states can also be prepared by controlled phase gate.[26] Some controlled phase gate schemes have been well designed in trapped neutral atoms.[27–32] In recent years, quantum entanglement and state transfer can be implemented experimentally in remote microwave cavity memories system.[33]

In the experiments of quantum computation and quantum information processing, some parameters fluctuations during the whole experimental process are inevitable and would decrease the performance of the scheme. The adiabatic evolution is a highly robust method[34] to deal with some parameter fluctuations. However, the adiabatic evolution takes a long time, so the target may be affected by noise and other factors that induce decoherence. In order to overcome the disadvantage, many accelerated schemes have been proposed.[35–65] The transitionless quantum driving (TQD) is one of the promising methods to accelerate the adiabatic evolution.[35–44] However, when we use this method to accelerate the evolution, we will encounter the difficulty that the initial state and the desired state or two energy levels in the original Hamiltonian are difficult to couple directly in experiment. Although the requirement for additional unaccessible ground-state couplings may be relaxed sometimes, the conditions on which the three-level system can be simplified to effective two-level system should be satisfied to further modify the pulses.[17,45] Another way to accelerate adiabatic evolution is Lewis–Riesenfeld invariants with pulse either needs infinite energy gap to be perfect, or cannot be opened or closed smoothly.[44,46–55,66]

Recently, Baksic et al. proposed a dressed state method to accelerate the adiabatic passage.[52] In dressed state scheme, the modified Hamiltonian of the coupling of two states, which is easily realized in experiment is introduced. Through two unitary transformations, the parameters of the modified Hamiltonian can be determined and the form of driving pulse can be obtained, which makes the scheme easy to implement in experiment. Based on the dressed states scheme, Kang et al. applied deressed state method to superconducting quantum interference devices to realize the fast preparation of W states;[53] Ban et al. indicated a design to fast create and transfer coherence in triple quantum dots by using the dressed state method;[54] Wu et al. proposed the schemes to accelerate state transfer and entanglement preparation and realize a fast CNOT gate all by using the dressed state method,[55,56] and so on.

Based on the above schemes, we propose effective schemes to realize the distributed quantum entanglement and state transfer by trapping two atoms in two different cavities in cavity–fiber–cavity system and coupled cavity system, and accelerate the implementation of the schemes by using the dressed state method. In this paper, the use of QED system can avoid the interaction of the applied fields. Beyond that, we give the expression of parameters used in the scheme of the dressed state by boundary conditions, and the expression of modified pulses obtained by the scheme of dressed state. Then, the pulse which is similar to the modified pulse and easy to realize in experiment is obtained by curve fitting. The results of numerical simulation show that our schemes have high fidelity and have good robustness to dissipation caused by photon leakage, spontaneous emission, and fluctuation of some parameters whether in coupled cavity system or in the cavity–fiber–cavity system. In a word, we propose fast schemes for the preparation of distributed quantum entanglement and state transfer.

The structure of this paper is arranged as follows: In Section 2, we briefly review the quantum Zeno dynamics. In Section 3, we introduce the scheme of state transfer and entanglement preparation in a coupled cavity system. In Section 4, we introduce the scheme of state transfer and entanglement preparation in cavity–fiber–cavity system. In Section 5, we analyze the influence of dissipation caused by spontaneous emission, photon leakage, and the fluctuation on fidelity. In Section 6, we come to the conclusion.

2. Basic theory about quantum Zeno dynamics

As we will use it below, let us briefly introduce quantum Zeno dynamics. We express the Hamiltonian that controls the evolution of quantum system as follows:

where Hobs can be regarded as the Hamiltonian of quantum system and Hmeas as an additional Hamiltonian equivalent to the measurement of a quantum system. K stands for coupling strength. When a strong coupling condition, K → ∞, is satisfied, the evolution operator of a system can be written as[67]

where Pn is the projection operator of Hmeas with eigenvalues λn (Hmeas = ∑n λnPn). It is worth noting that the system will evolve in the Zeno subspace where the initial state is located. It is precisely shown that this characteristic of quantum Zeno dynamics greatly simplifies the problem.

3. Preparation of entangled states and state transfer in coupled cavity system
3.1. The coupled cavity model

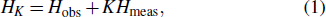
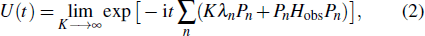
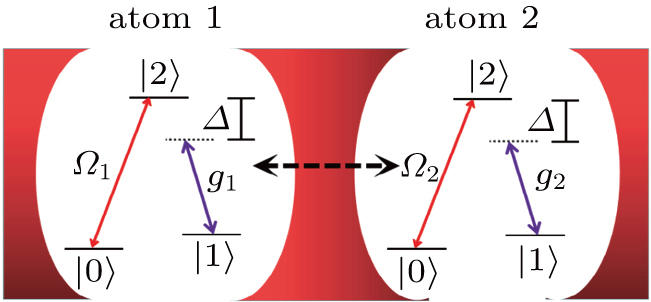
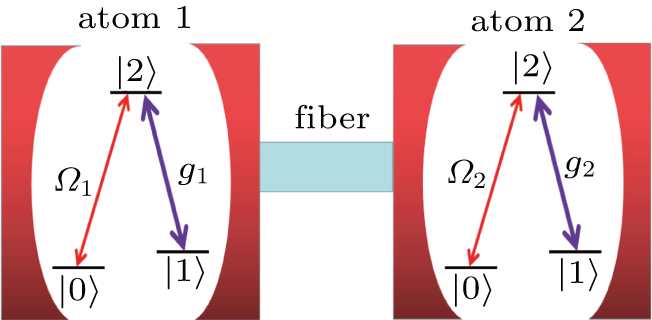
As shown in Fig. 1, two identical Λ-type atoms are trapped in the corresponding optical cavities, and the two cavities can be directly coupled. Each one has two ground states |0⟩ and |1⟩ and one excited state |2⟩. The Hamiltonian of the system can be written as (ħ = 1)

where HS (HI) is the Hamiltonian of internal system (interaction between external applied field and atoms). The ωi (i = 0,1,2), and ωa identify the energy of level i, and the photon energy in the cavity 1 or 2 separately. (aj) is the photon creation (annihilation) operator in cavity j (j = 1,2). The Ωj(t) and gj represent the external laser field applied to the cavity j and coupling strength between energy levels |1⟩ and |2⟩ in cavity j (j = 1, 2). The χ is the photon transfer strength between coupling cavities. To simplify the matter, we set g1 = g2 = g, ωa = ω, and introduce a detuning: Δ = ω2 − ω1 − ω. We introduce two bosonic modes c+ and c- as follows:[68] , . By substituting the bosonic modes into HS we have

As you can see from Eq. (4), this system can be regarded as two kinds of c+ and c- photons with the corresponding frequencies ω + χ and ω − χ in one cavity and these photons interact with atoms in this cavity. In interaction picture, equation (4) becomes

When Δ = χ and Δ + χ ≫ g, equation (5) can be reduced to

Fig. 1. As shown in the figure, the two atoms are trapped in two separate cavities which can be coupled directly, and the coupling strength is χ. In addition, the two atoms have the same three-level structure, two ground states |0⟩, |1⟩, and one excited state |2⟩ corresponding to energy ω0, ω1, and ω2 respectively, and the energy levels |0⟩ and |2⟩ of atom 1 (2) are coupled by adding laser Ω1(2)(t), and the energy levels |1⟩ and |2⟩ are coupled by cavity, and the coupling strength is g1 (2). Here, the detuning between energy levels |1⟩ and |2⟩ is equal to Δ.

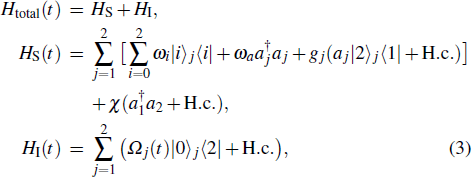
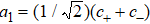
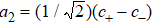
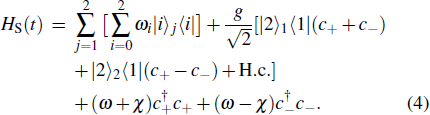
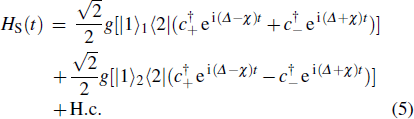
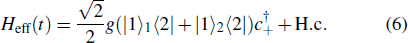
We put the system in state |0⟩1|1⟩2|1⟩c at t = 0. Therefore, the total system will evolve in the following Hilbert space:

Apparently, this system is in a state where the eigenvalue is equal to 0 at t = 0. Under the Zeno limit condition Ω1(t), Ω2(t) ≪ g, this system almost evolves in the dark state subspace of Heff, and this subspace can be represented as

where the state . The projection operator of can be represented as

According to Eq. (2), the total Hamiltonian Htotal(t) is nearly

Here, , . Then ΩA(t) and ΩB(t) can be chosen as[55]

where we make and θ(t) = − arctan(ΩA(t)/ΩB(t)). By calculations, we can obtain the eigenstates of H(t)

with the eigenvalues λd = 0 and λ± = ± Ω(t), separately. In order to clearly describe the evolution of the system, we choose a new set of {|ϕ1⟩, |ϕd⟩, |ϕ5⟩ defined by a unitary transformation

Under the new basis, the H(t) changes to

In order to eliminate the error caused by the non-adiabatic term and shorten the operation time, we choose a modified Hamiltonian Hc,

We can see from the expression of Eq. (16) that there is no direct coupling between |ϕ1⟩ and |ϕ5⟩. The direct coupling between |ϕ1⟩ and |ϕ5⟩ is difficult to realize in the experiment. Here, gx(t) and gz(t) are time-dependent parameters; , , and are spin-1 operators. The general form of the spin-1 operators can be written as

The Hamiltonian of the system with Hc addition is

In order to express the influence of Hc on system evolution more clearly, we introduce a new unitary operator with Euler angles η(t), μ(t), and ξ(t),

and |φ±,d(t)⟩ = V†(t)|ψ±,d⟩. After the unitary transformation, H1(t) + Hc(t) is

The condition for diagonalizing H2(t) is that the gx and gz must be chosen as

From Ref. [52], we know that μ(ti) and μ(tf) must be equal to 0, and the other two Euler angles can have arbitrary values. For the sake of simplicity, we choose ξ(t) = η(t) = 0. In the case,

The entire system will evolve along the state |ψd(t)⟩. As a result, when θ(ti) = 0, θ(tf) = π/2, μ(ti) = 0, and μ(tf) = 0, the state transfer |ϕ1⟩ → |ϕ5 ⟩ = |0⟩1|1⟩2|0⟩c → |1⟩1|0⟩2|0⟩c is carried out; when θ(ti) = 0, θ(tf) = π/4, μ(ti) = 0, and μ(tf) = 0, the preparation of entangled state is carried out. Here, ti is the initial time and tf is the final time, and the same below.

3.2. The design pulse

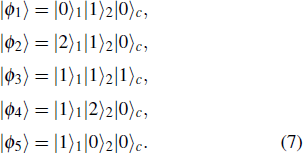
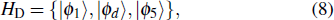
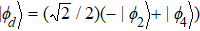
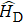
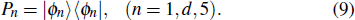
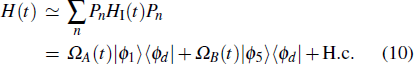
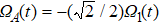
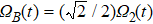
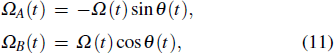
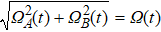
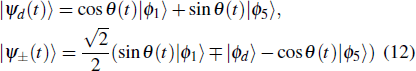
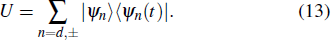
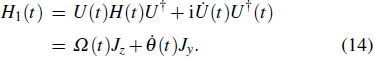
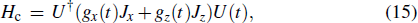
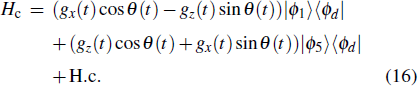
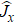
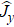
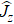
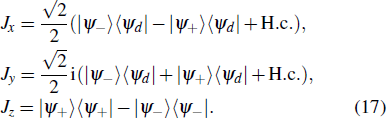
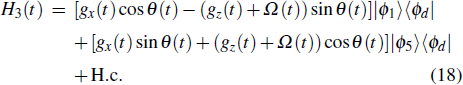
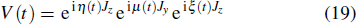
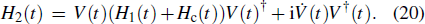
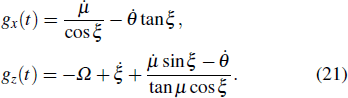
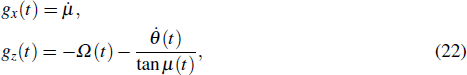
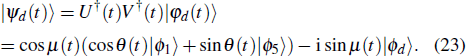
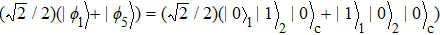
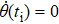
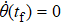
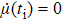
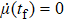
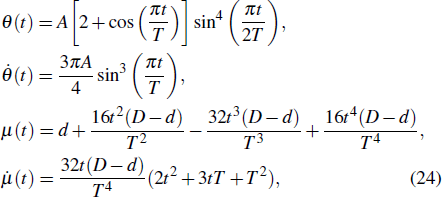
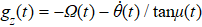
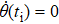
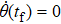
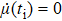
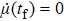
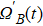
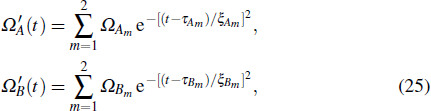
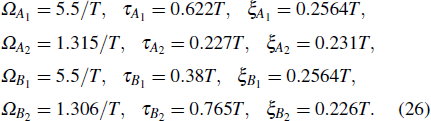
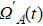
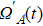
In order to realize state transfer and smooth opening and closing of parameters, the conditions: θ(ti) = 0, θ(tf) = π/2, μ(ti) = 0, μ(tf) = 0, and , , , must be met. As a result, we choose the parameters as follows:

where μ(ti) = μ(tf) ≈ 0, because , μ(t) ≠ 0. The population of |ϕd⟩ decreases with the maximum value of μ(t). But when μ(t) decreases, T (where T is the interaction time) will increase when the value of pulses amplitute Ω(t) is determined.[53] Because of the above contradictions, we choose the appropriate parameters: A = π/2, d = 0.001, D = 0.5, where sin2(μ(t)) ≤ 0.23. From the above analysis, the form of ΩA(t) and ΩB(t) is so complex that it is difficult to achieve it experimentally. Therefore, we use the superposition of two Gaussian pulses which is easy to realize in experiment to replace ΩA(t) and ΩB(t), and the parameters of the two Gaussian pulses can be determined by numerical simulations. Similar to state transfer, when we want to generate entangled states, the boundary condition becomes θ(ti) = 0, θ(tf) = π/4, μ(ti) = 0, μ(tf) = 0, , , , , and the parameters can be selected as A = π/4, d = 0.001, D = 0.25. When state transfer is realized, the form and parameters of the two Gaussian pulses , can be selected as

When the entangled state is prepared, the parameters of the two Gaussian pulses , can be chosen as

In order to compare two kinds of pulses, we plot , ΩA(t), , and ΩB(t) versus t/T in Figs. 2 and 3.

Fig. 2. The pulses , ΩA(t), , and ΩB(t) versus t/T for realizing state transition.
Fig. 3. The pulses , ΩA(t), , and ΩB(t) versus t/T for preparing entangled state.
3.3. Numerical simulations

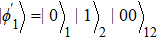
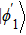
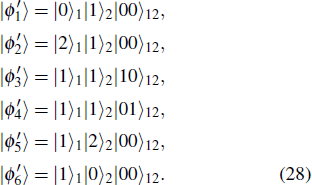
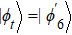
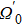
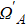
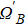
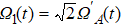
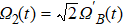
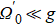
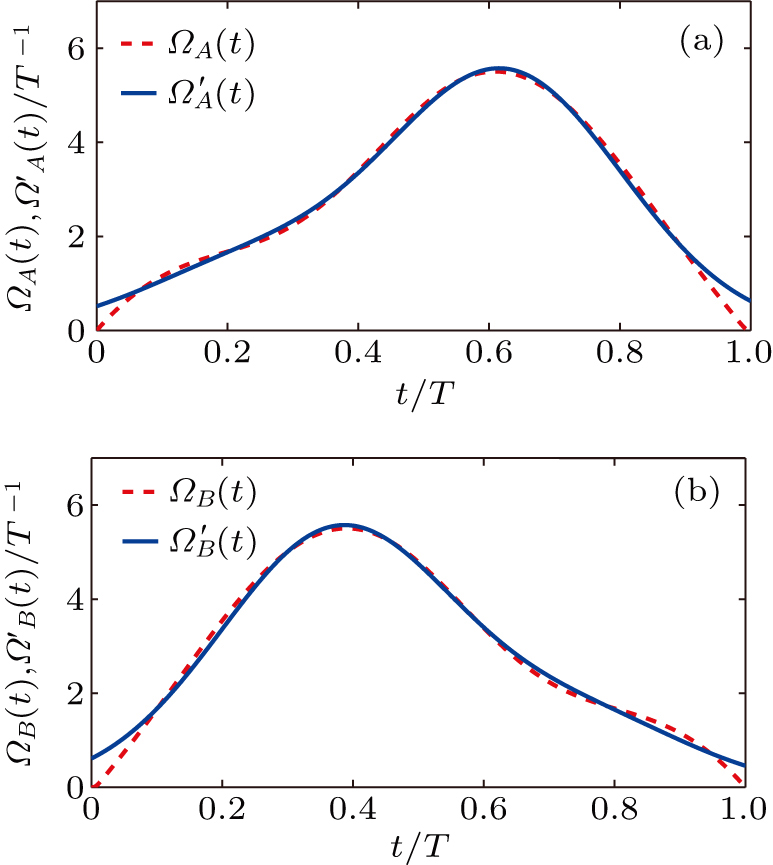
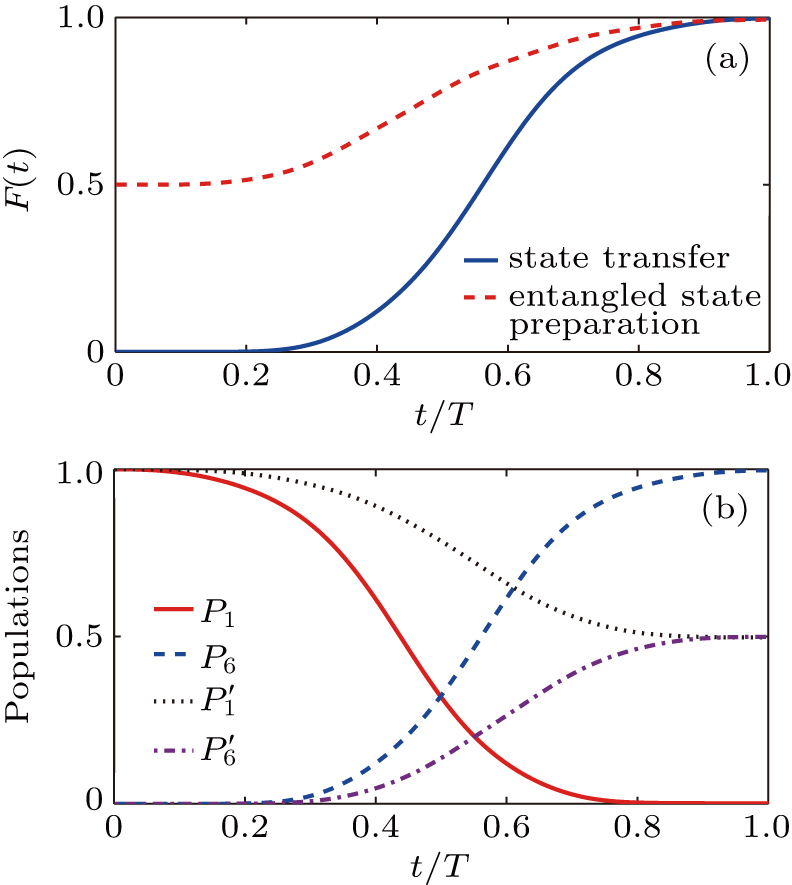
In this section, we make numerical simulations with the Hamiltonian of Eq. (3) to determine some parameters. We choose the initial state of the system as , where means that atom 1 is in |0⟩, atom 2 is in |1⟩, and cavity 1 and cavity 2 are all in the vacuum state. This system will evolve in the Hilbert space

As is known to all, the fidelity F(t) = ⟨ϕt|ρ(t)|ϕt⟩. For realizing state transfer, the state . The maximum value of the amplitude of pulses for state transfers and in the range of time 0 to T is approximately equal to 7.89/T (in other words, , ), and the Zeno limit condition becomes . Besides, in order to satisfy the condition of large detuning, |χ|≫ g/2 must be set. However, there are great experimental limitations on the maximum values of g and v. As shown in Fig. 4(a) and Fig. 4(b), even if the above two conditions are not strictly met, the fidelity can almost reach 1. Where, we choose g/T = 20, χ/T = 400 for numerical simulations.

Fig. 4. In the coupled cavity system, (a) the fidelity of state transfer versus g/T and χ/T; (b) the fidelity of entangled state preparation versus g/T and χ/T; (c) the fidelity of state transfer versus δ g/g and δ χ/χ (where g = 20T, χ = 400T); (d) the fidelity of entangled state preparation versus δ g/g and δ χ/χ (where g = 35T, χ = 400T).

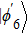
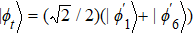
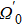
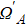
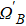
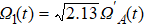
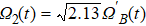
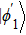
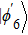
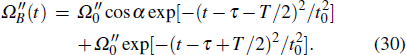
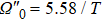
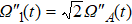
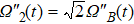
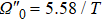
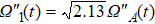
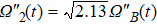
In order to prove the feasibility of our scheme, we plot the fidelity and population via the numerical simulations in Fig. 5. Seen from Fig. 5(a), when t/T ≥ 0.95, the fidelity F(t)≈ 1. Figure 5(b) shows the populations in the evolution process, and it can be seen that the population of is no less than 0.99 when t/T = 1. Similar to state transfer, when entangled state is prepared, the state . In order to achieve the goal better, we can increase laser intensity appropriately. The maximum value of the amplitude of the corresponding pulses and in the range of time 0 to T is approximately equal to 9.86/T (that is to say, , ). And we choose g/T = 35 and χ/T = 400 in the preparation of entangled states. In addition, we study the effect of g and χ fluctuations on fidelity in Fig. 4(c) and Fig. 4(d). From Fig. 4(c) and Fig. 4(d) we can see that the fidelities of the state transition and entangled state preparation can still be larger than 0.984 and 0.993 when the values of g and χ are in the range of −0.1 to 0.1. Figure 5(b) shows that the populations of and in the evolution process are almost equal to 0.5, and the fidelity F(t) ≈ 1 when t/T = 1. In order to better compare the dressed state method with the traditional STIRAP method, we introduce the following Gaussian pulses:[69,70]

The parameters can be chosen as: τ = 0.1T and t0 = 0.15T. When we want to achieve the goals of state transfer and entanglement preparation, α = π/2, , , , and α = π/4, , , , respectively. Where T′ is the operating time when using the classical pulse. As we can see from Fig. 6, the dressed state method is nearly four times faster than the Gaussian pulse method in the preparation of entangled state, especially nearly nine times faster in the realization of state transfer. So, our scheme has been effectively accelerated by the dressed state method.

Fig. 5. (a) The fidelities of state transfer and entangled state preparation versus t/T. (b) The populations of state transfer and entangled state preparation versus t/T. P1 () and P6 () are the populations of and for state transfer (entangled state preparation) with the related parameters: g/T = 20, χ/T = 400 (g/T = 35, χ/T = 400).
Fig. 6. The fidelities of state transfer and the preparation of entangled states versus T′/T (T′ is the operating time when using the classical pulse) in the coupled cavity system by using the STIRAP method. The parameters: τ = 0.1T, t0 = 0.15T. The related parameters for state transfer (entangled state preparation): α = π/2, (α = π/4, ). The other related parameters used for state transfer and the preparation of entangled state are the same as those used in Fig. 5.
4. Quantum state transfer and preparation of entanglement in cavity–fiber–cavity system
4.1. The cavity–fiber–cavity model

As shown in Fig. 7, two identical Λ-type atoms are trapped in the corresponding optical cavities connected by a fiber. If the short fiber limit (lν)/(2π c) ≪ 1 is satisfied, only the resonant modes of the fibers interact with the cavity modes,[71] where l, ν, and c are the length of the fiber, the decay rate of the cavity field into a continuum of fiber modes, and the speed of light, respectively. Each one has two ground states |0⟩ and |1⟩ and one excited state |2⟩.

Fig. 7. As shown in the figure, two atoms trapped in an optical cavity are connected by an optical fiber with a strength of η. In addition, the two atoms have the same three-level structure, two ground states |0⟩, |1⟩, and one excited state |2⟩ corresponding to energies ω0, ω1, and ω2 respectively, and the energy levels |0⟩ and |2⟩ of atom 1 (2) are coupled by adding laser Ω1 (2)(t), and the energy levels |1⟩ and |2⟩ are coupled by cavity, and the coupling strength is g1(2). Here, the detuning between energy levels |1⟩ and |2⟩ is equal to 0.

The Hamiltonian of the system can be written as (ħ = 1)

where HS (HI) is the Hamiltonian of internal system (interaction between external applied field and atoms). The ωi (i = 0,1,2), ωa and ωb identify the energy of level i, the photon energy in the cavity 1 or 2 and the fiber separately. (aj) is the photon creation(annihilation) operator in the cavity j (j = 1,2) and b† (b) is the photon creation (annihilation) operator in the fiber. The Ωj(t) and gj represent the external laser field applied to the cavity j and coupling strength between energy levels |1⟩ and |2⟩ in cavity j (j = 1, 2). The η is the coupling strength between the mode in the fiber and the modes in the cavities. To simplify the matter, we set g1 = g2 = g. There is an easy way to judge ωa = ωb, and set ωa = ωb = ω. We introduce three bosonic modes[71] c± and c0 as follows: , , and . By substituting the bosonic modes into HS, we obtain

As we can see from Eq. (32), this system can be regarded as three kinds of c+, c0, and c- photons with the corresponding frequencies , ω, and in one cavity and these photons interact with atoms in this cavity. In the interaction picture, equation (32) becomes

where Δ = ω2 − ω1. When Δ = ω, equation (33) becomes

In the context of , equation (34) can be reduced to

We put the system in the state |0⟩1|1⟩2|1⟩c at t = 0. Therefore, the total system will evolve in the following Hilbert space:

Apparently, this system is initially in a state with eigenvalue 0. Under the Zeno limit condition of Ω1(t), Ω2(t) ≪ g, this system almost evolves in the dark state subspace of Heff, and this subspace can be represented as

where the state , the projection operator of can be represented as

According to Eq. (2), Htotal(t) is nearly

here, , . Then ΩA(t) and ΩB(t) can be chosen as[55]

where we make and θ(t) = arctan(ΩA/ΩB), and by calculatons, we can obtain the eigenstates of H(t)

with the eigenvalues λd = 0 and λ± = ± Ω(t), separately. In order to clearly describe the evolution of the system, we choose a new set of {|ϕ1⟩, |ϕd⟩, |ϕ5⟩ defined by a unitary transformation

Under the new basis, the H(t) changes to

In order to eliminate the error caused by the non adiabatic term and shorten the operation time, we choose a modified Hamiltonian Hc,

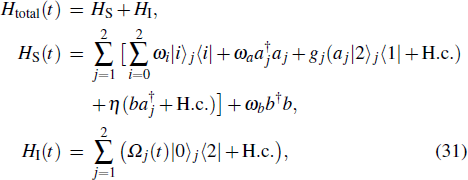
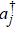
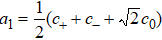
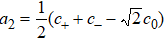
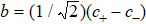
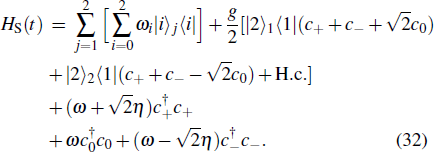
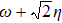
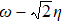
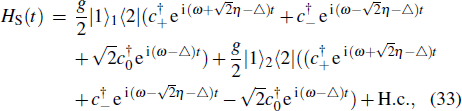
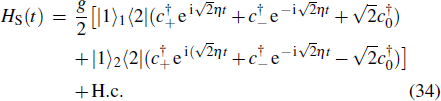
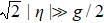
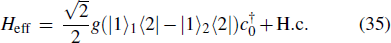
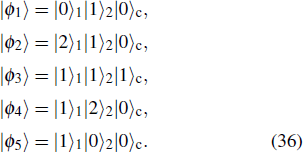
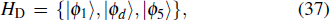
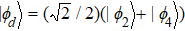
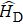
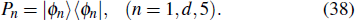
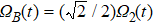
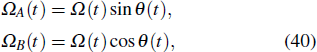
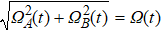
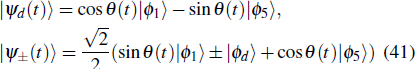
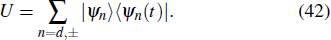
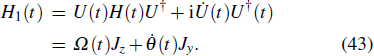
We can see from the expression of Eq. (45) that there is no direct coupling between |ϕ1⟩ and |ϕ5⟩. The direct coupling between |ϕ1⟩ and |ϕ5⟩ is difficult to realize in experiments. Here, gx(t) and gz(t) are time-dependent parameters; , , and are spin-1 operators. The general form of the spin-1 operators can be written as

The Hamiltonian of the system with Hc addition is

In order to express the influence of Hc on system evolution more clearly, we introduce a new unitary operator with Euler angles η(t), μ(t), and ξ(t)[52]

and |φ±,d(t)⟩ = V†(t)|ψ±,d⟩. After the unitary transformation, H1(t) + Hc(t) becomes

The condition for diagonalizing H2(t) is that gx and gz must be obtained as

From Ref. [52], we know that μ(ti), μ(tf) must be equal to 0, and the other two Euler angles can have arbitrary values. For the sake of simplicity, we choose ξ(t) = η(t) = 0. In the case,

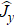
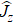
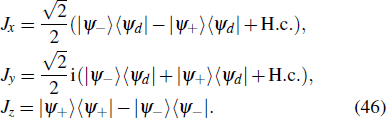
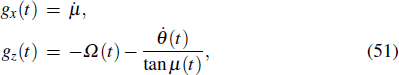
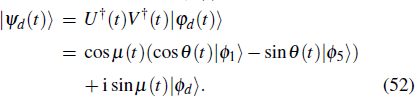
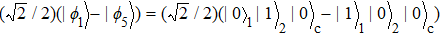
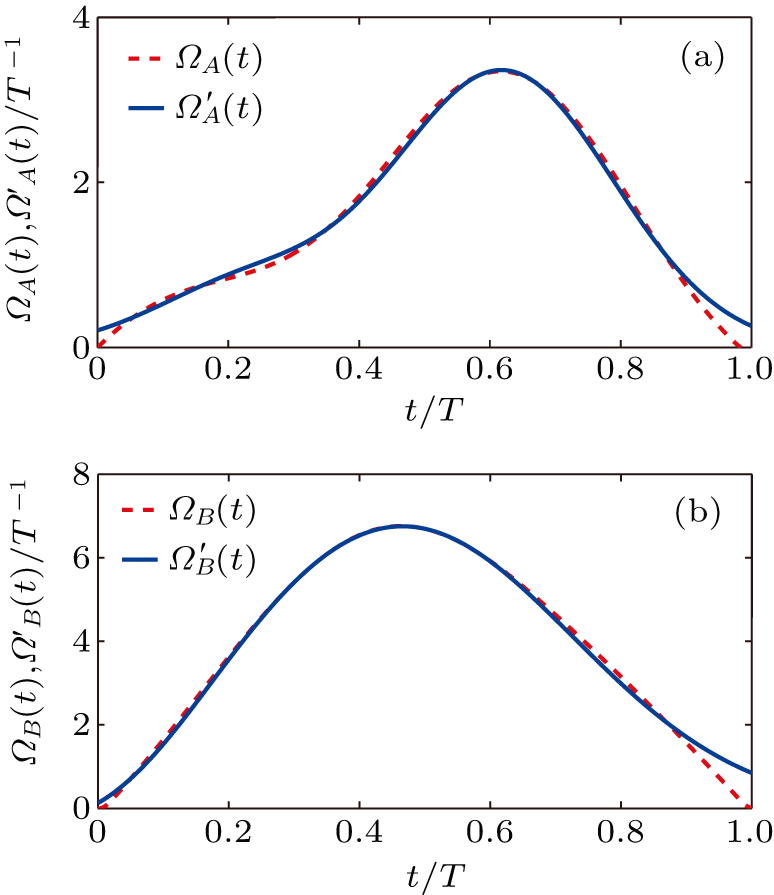
The entire system will evolve along the state |ψd(t)⟩. As a result, when θ(ti) = 0, θ(tf) = π/2, μ(ti) = 0, and μ(tf) = 0, the state transfer |ϕ1⟩ → − |ϕ5⟩ = |0⟩1|1⟩2|0⟩c→ − |1⟩1|0⟩2|0⟩c is carried out; when θ(ti) = 0, θ(tf) = π/4, μ(ti) = 0, and μ(tf) = 0, the preparation of entangled state is carried out.

4.2. Numerical simulations

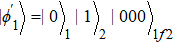
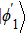
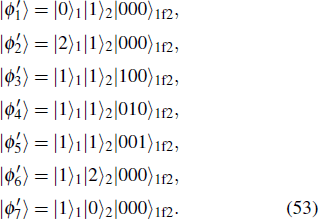
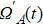
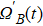
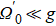
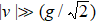
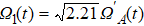
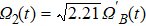
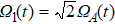
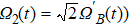
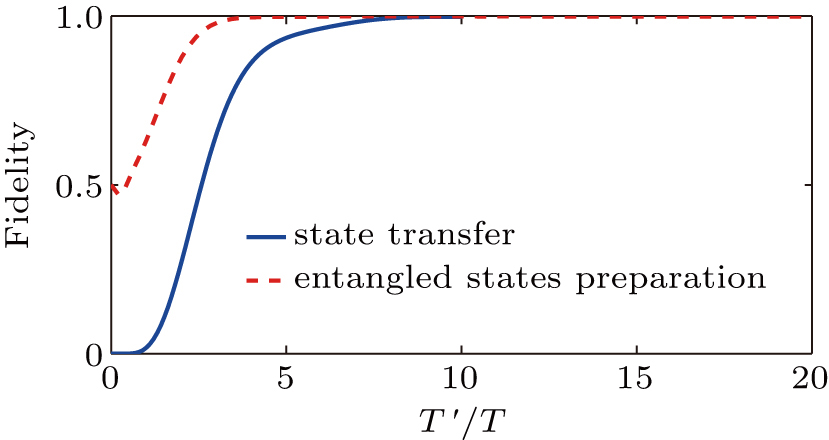
In this section, we make numerical simulations to determine some parameters. We choose the Hamiltonian of Eq. (31) and the initial state of the system as , where means that atom 1 is in |0⟩, atom 2 is in |1⟩, and cavity 1, fiber, and cavity 2 are all in the vacuum state. This system will evolve in the Hilbert space to

Here, the laser is also and . In Figs. 8(a) and 8(b), we plot the fidelity of the entangled state and the state transfer versus g/T and v/T respectively. Here, the quantum Zeno limit condition is also , but the large detuning condition becomes . Figures 8(a) and 8(b) show that the fidelity is still close to 1 even when these two conditions are not well satisfied. Different from the schemes in the coupled cavity system, we choose parameters g/T = 30, v/T = 200 both for entanglement preparation and state transfer. The maximum value of the amplitude of pulses is 10/T (in other words, , ) for entanglement preparation and 7.89/T (that is to say, , for state transfer. In addition, we study the effect of g and η fluctuations on fidelity in Figs. 8(c) and 8(d). From Figs. 8(c) and 8(d) we can see that the fidelity of state transition and the fidelity of entangled state preparation are still larger than 0.999 and 0.997 when the values of g and v are in a range from −0.1 to 0.1.

Fig. 8. In the cavity–fiber–cavity system: (a) fidelity of state transfer versus g/T and v/T; (b) fidelity of entangled state preparation versus g/T and v/T; (c) fidelity of state transfer versus δ g/g and δ v/v (where g = 30T, v = 200T); (d) fidelity of entangled state preparation versus δ g/g and δ v/v (where g = 30T, v = 200T).

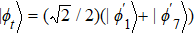
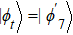
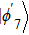
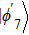
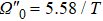
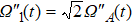
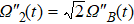
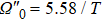
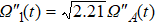
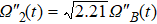
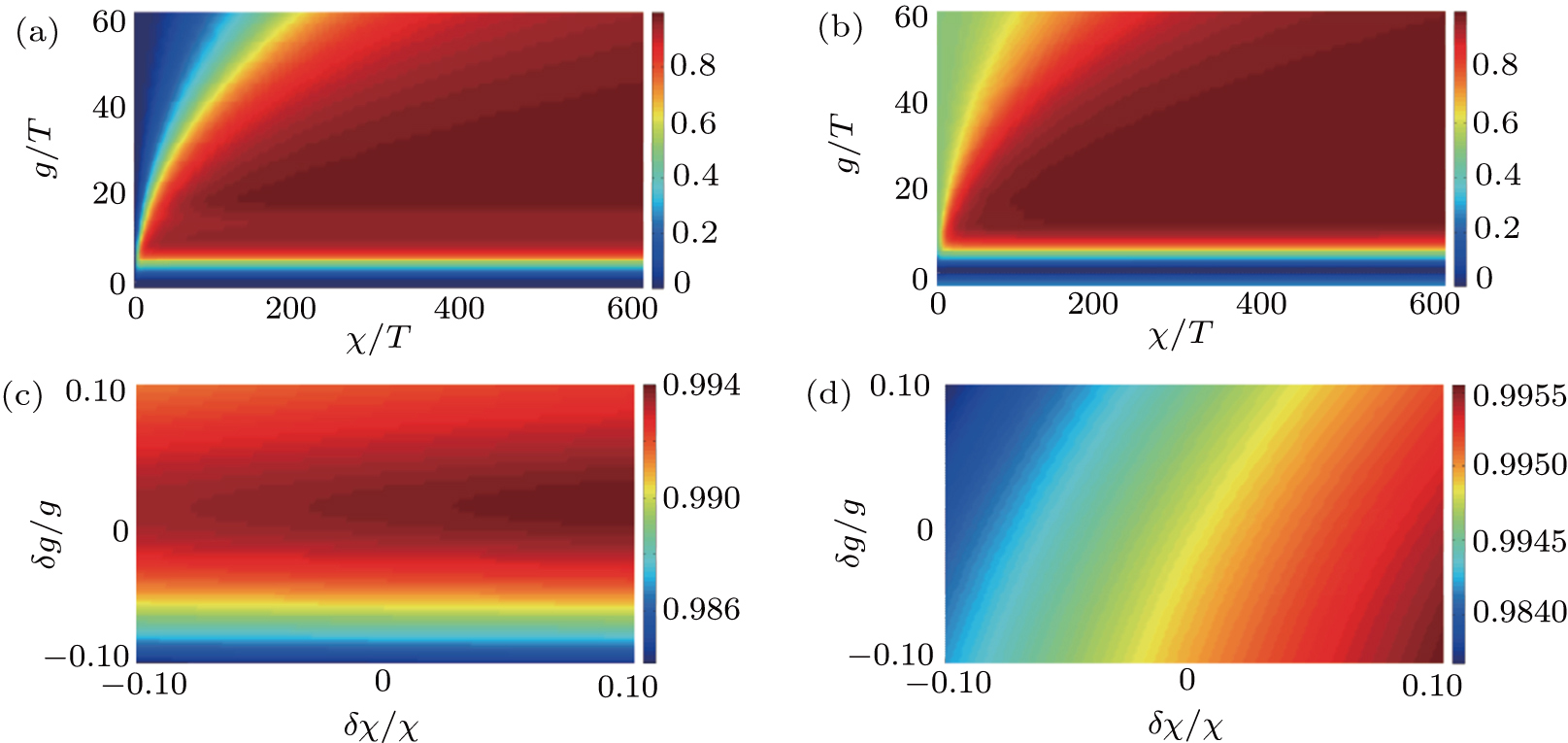
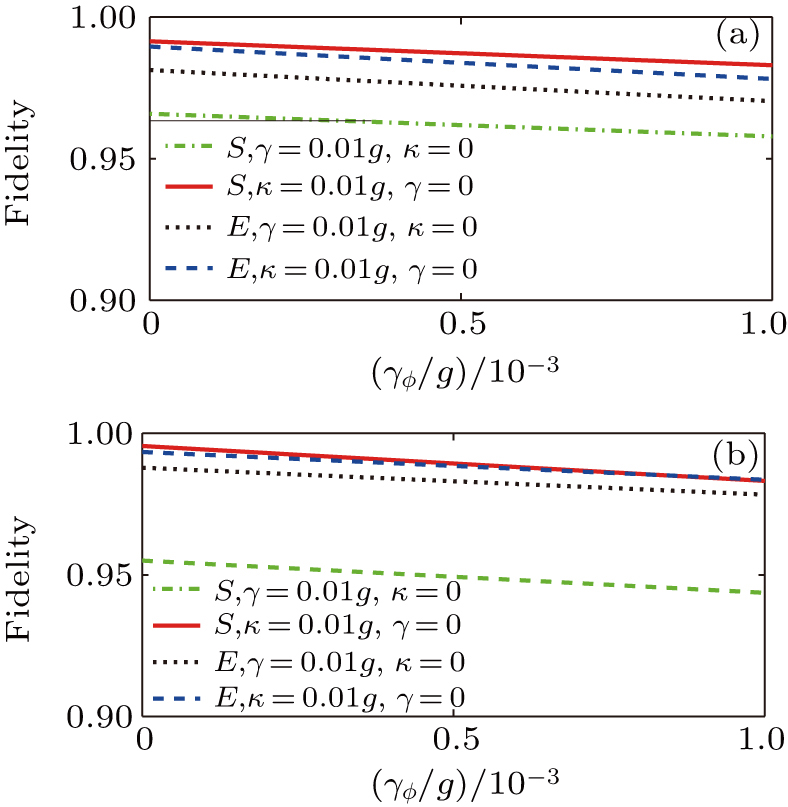
As shown in Fig. 9(a), the fidelities of the preparation of entangled states () and the state transfer () are larger than 0.99 when T/t = 1. As we can see in Fig. 9(b), when state transfer is realized, the population of is no less than 0.99, and when the entangled state is prepared, the populations of and in the evolution process are almost equal to 0.5 at t/T = 1. We also use the same method to compare the evolution time with the Gauss pulse method and the dressed state method. The pulses used here are somewhat different from those used in the coupled cavity system. When we want to achieve the goals of state transfer and entanglement preparation, α = π/2, , , , and α = π/4, , , respectively. Where T′ is the operating time when using the classical pulse. Figure 10 shows, the dressed state method is nearly four times faster than the Gauss pulse method in the preparation of entangled state, especially nearly nine times faster in the realization of state transfer. Therefore, the dressed state scheme is also suitable for the cavity–fiber–cavity system.

Fig. 9. (a) The fidelities of state transfer and entangled state preparation versus t/T, (b) the populations of state transfer and entangled state preparation versus t/T. P1 () and P7 () are the populations of and for state transfer and entangled state preparation with the related parameters: g/T = 30, η/T = 200.
Fig. 10. The fidelity of state transfer and the preparation of entangled states versus T′/T (T′ is the operating time when using the classical pulse) in the cavity–fiber–cavity system by using the STIRAP method. The parameters: τ = 0.1T, t0 = 0.15T. The related parameters for state transfer (entangled state preparation): α = π/2, (α = π/4, ). The other related parameters used for state transfer and the preparation of entangled state are the same as those used in Fig. 9.
5. The influence of dissipation and parameter fluctuation on fidelity

In this section, we consider the influence of photon leakage from cavity or fiber and atomic spontaneous emission on fidelity. These dissipations are experimentally unavoidable. When these dissipations are considered, the evolution of the whole system can be described by the following master equation:

where κA, κB, and κf are the photon leakage rates of cavity modes in cavity A, B, and fiber, respectively. γA (γB) is spontaneous emission rate of atom A (B) from excited state |2⟩ to ground states |0⟩ or |1⟩, where . is the dephasing rate, and ρi,j = (|2⟩i⟨ 2| − |j⟩i⟨ j|). Where i stands for atom i (i = A, B) and energy level j (j = 0, 1). For simplicity, we set , , and . Where, we choose the same parameters and laser in coupled cavity and cavity–fiber–cavity system as above to realize the state transfer and the preparation of entangled states, and draw their fidelity versus κ/g and γ/g through Eq. (54) in Fig. 11.

Fig. 11. (a) The fidelity of state transfer versus κ/g and γ/g in the coupled cavity system; (b) the fidelity of entangled state preparation versus κ/g and γ/g in the coupled cavity system; (c) the fidelity of state transfer versus κ/g and γ/g in the cavity–fiber–cavity system; (d) the fidelity of entangled state preparation versus κ/g and γ/g in the cavity–fiber–cavity system. In Figs. 11(a) and 11(b), the related parameters used for state transfer and entangled state the preparation are the same as those used in Fig. 5. In Figs. 11(c) and 11(d), the related parameters used for state transfer and entangled state preparation are the same as those used in Fig. 9.

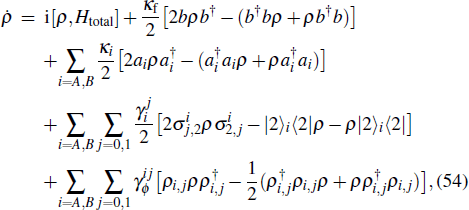
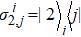
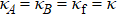
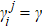
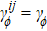
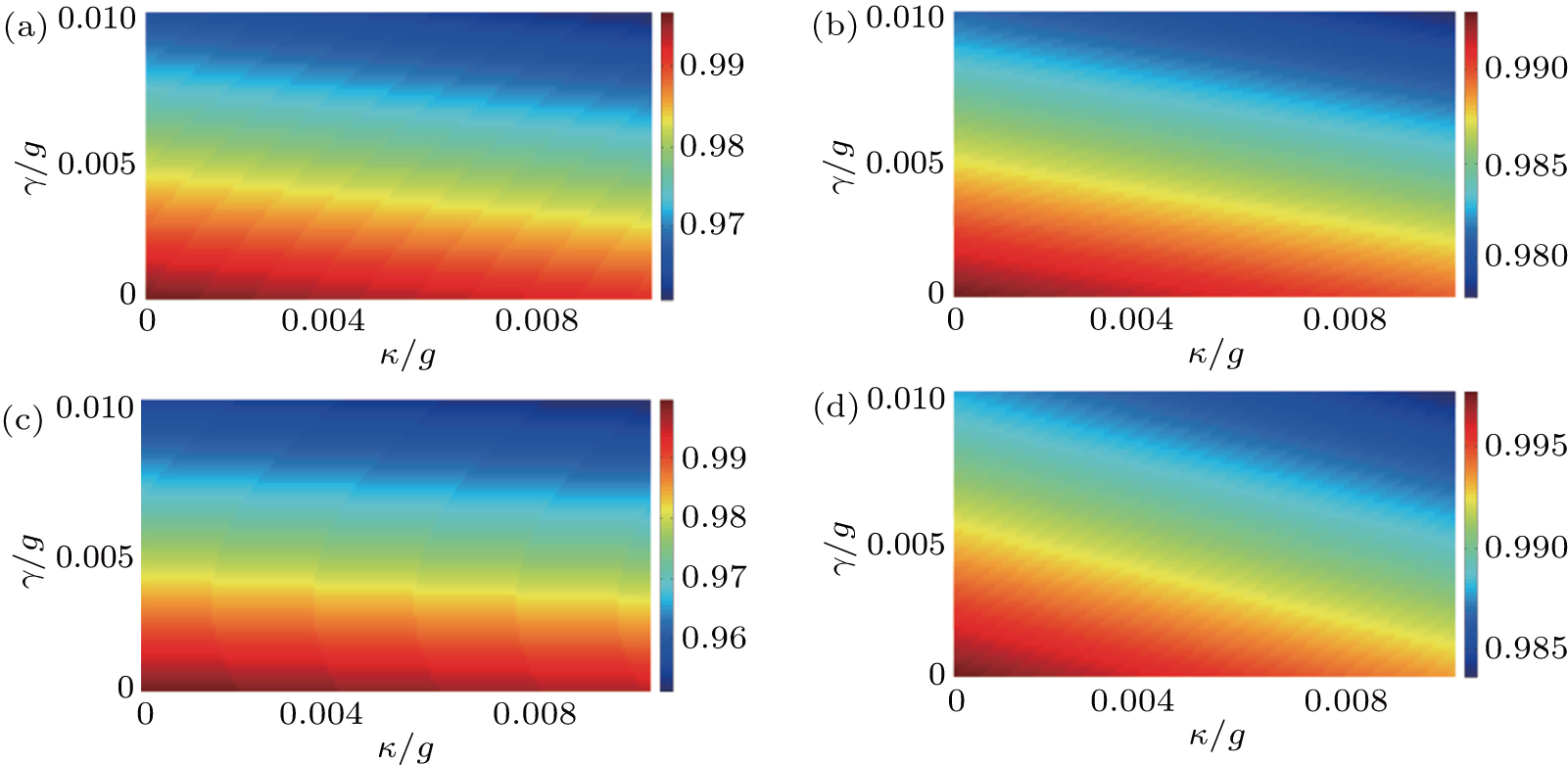
As shown in Fig. 11, in coupled cavity system, when state transfer is realized and the preparation of entangled states, the fidelity is about 0.96 and 0.976 and in cavity–fiber–cavity system, when state transfer is realized and the preparation of entangled states, the fidelity is about 0.95 and 0.97 even when both κ/g and γ/g are 0.01 when dissipation is considered. Besides, it can be seen from Fig. 11 that the influence of spontaneous emission on fidelity is greater than that of photon leakage in the cavity–fiber–cavity system or coupled cavity system, whether in the realization of state transfer or in the preparation of entangled state. Dephasing is a very troublesome decoherence factor.[72] Therefore, we study the effect of dephasing on the fidelity of coupled cavity and cavity–fiber–cavity system in Fig. 12. When γ = 0.01g, κ = 0, and γϕ = 0.001g, it can be seen from Fig. 12(a) that in the coupled cavity system, the fidelities of state transfer and the preparation of entangled state are 0.957 and 0.97 respectively. When κ = 0.01g, γ = 0, and γϕ = 0.001g, it can be seen from Fig. 12(a) that in the coupled cavity system, the fidelities of state transfer and the preparation of entangled state are 0.983 and 0.978 respectively. When γ = 0.01g, κ = 0, and γϕ = 0.001g, it can be seen from Fig. 12(b) that in the cavity–fiber–cavity system, the fidelities of state transfer and the preparation of entangled state are 0.943 and 0.978 respectively. When κ = 0.01g, γ = 0, and γϕ = 0.001g, it can be seen from Fig. 12(b) that in the cavity–fiber-cavity system, the fidelities of state transfer and the preparation of entangled state are 0.9832 and 0.9836 respectively. Therefore, our scheme is robust to decoherence.

Fig. 12. (a) the fidelity versus γϕ/g in the coupled cavity system, and the related parameters used for state transfer and entangled state preparation are the same as those used in Fig. 5; (b) the fidelity versus γϕ/g in the cavity–fiber–cavity system, and the related parameters used for state transfer and entangled state preparation are the same as those used in Fig. 9. In the figure above, S and E represent the state transfer and the preparation of entangled states, respectively.

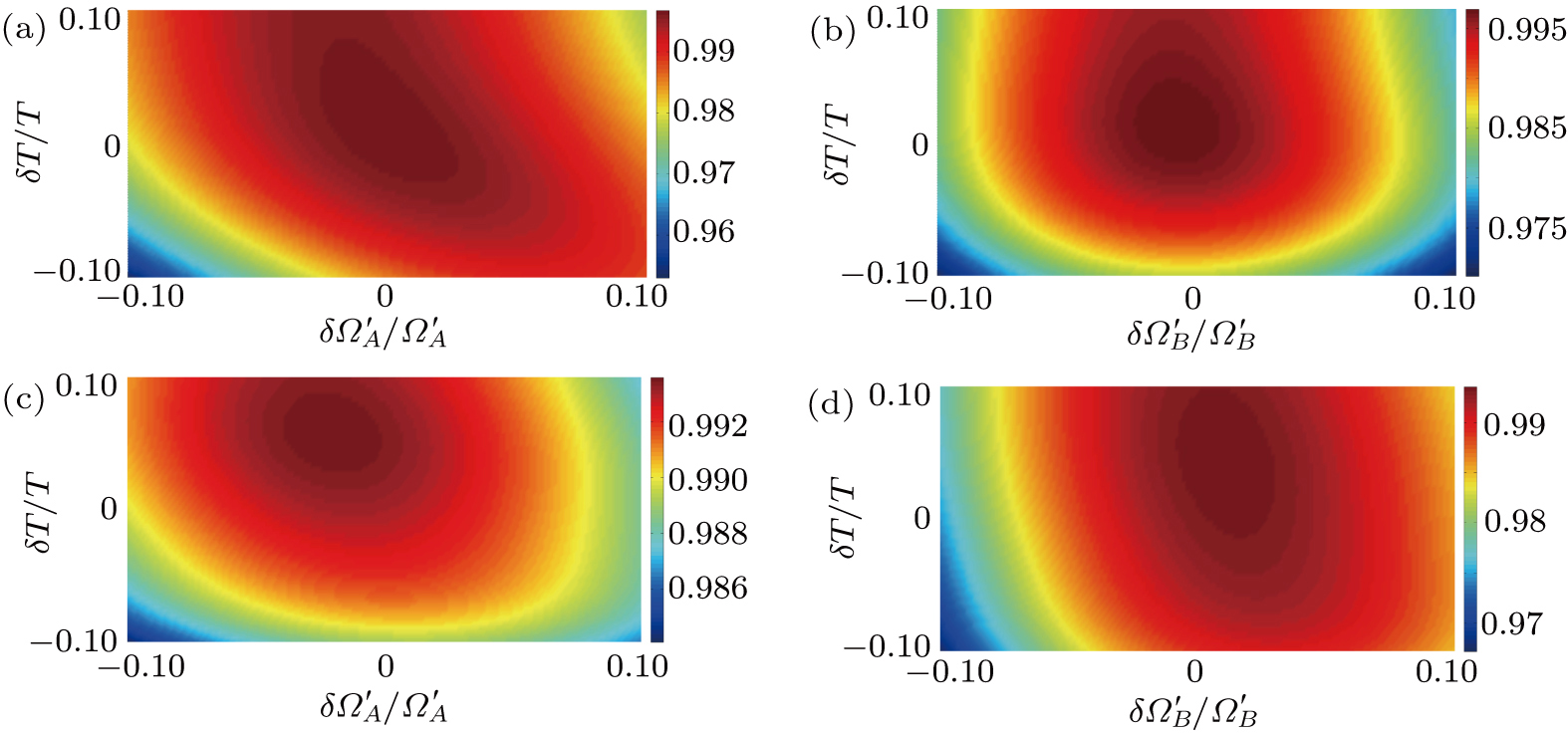
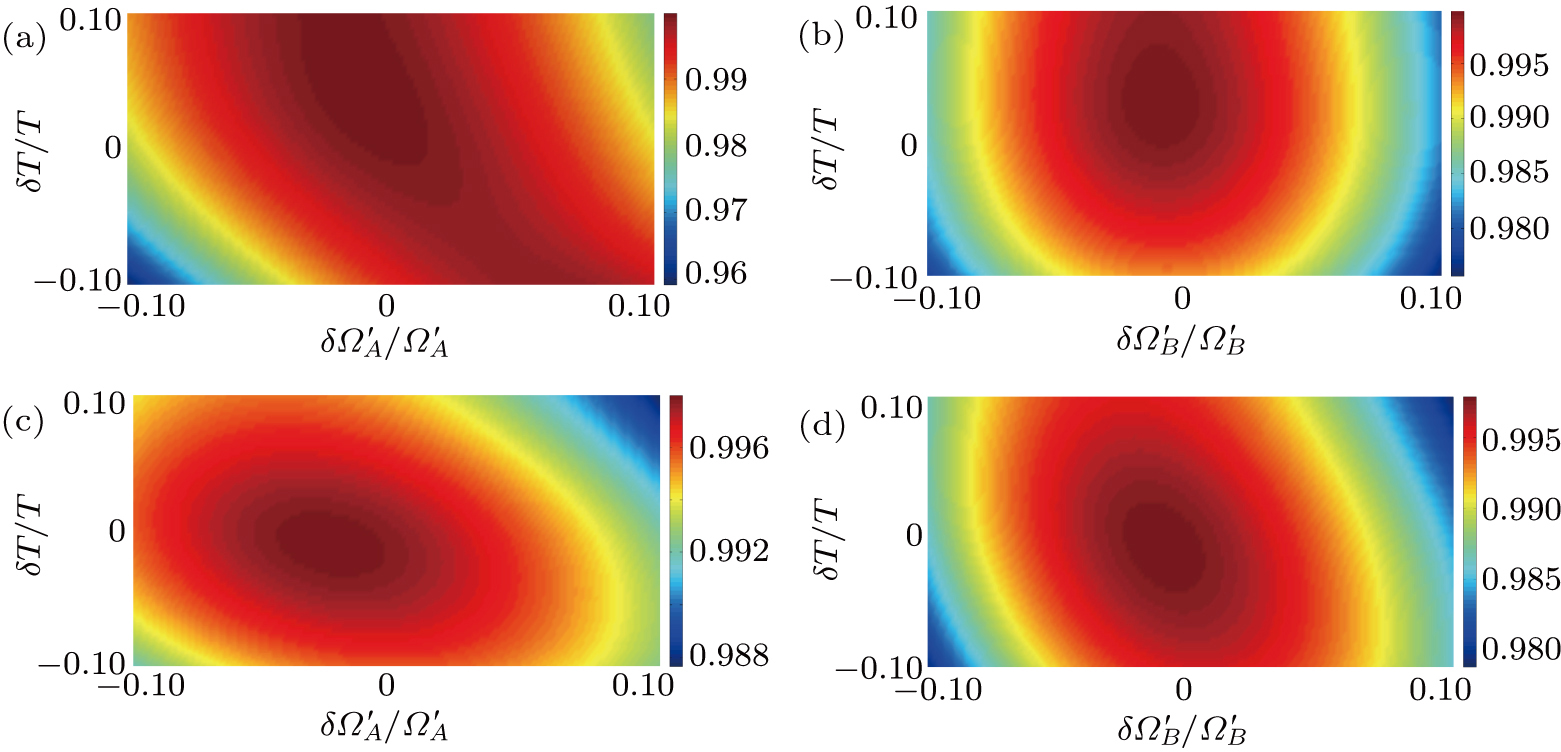
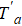
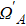
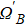
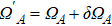
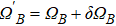
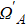
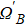
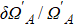
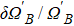
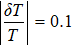
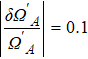
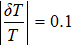
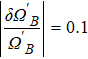
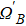
In addition, the fluctuations of some parameters are also inevitable in practical experiments. Therefore, we also study the influence of some parameter fluctuations on fidelity. We assume that the actual operating time is , the actual laser intensity is and , and , , . Because the laser we choose is the superposition of two Gaussian pulses, we use the fluctuation amplitude of the operation time of the two Gaussian pulses and and correspond to the laser intensity for state transfer or the preparation of entangled states in coupled cavity or cavity–fiber–cavity system. As a result, in Figs. 13 and 14, we show the fidelity varies with δ T/T, , and . It can be seen from Figs. 13(a),13(c),14(a), and 14(c), in the coupled cavity system, even if the parameter fluctuates within and , the fidelity of state transfer is larger than 0.9529 and the fidelity of entanglement preparation is larger than 0.9841, respectively. While in cavity–fiber–cavity system with the same parameter fluctuations, the corresponding fidelities are larger than 0.959 and 0.9876. Similarly, it can be seen from Figs. 13(b),13(d),14(b), and 14(d), in the coupled cavity system, even if the parameter fluctuates within and , the fidelities of state transfer and entanglement preparation are still larger than 0.9701 and 0.9671, respectively. While in cavity–fiber–cavity system with the same parameter fluctuations, the corresponding fidelities are larger than 0.9756 and 0.9788. According to Figs. 13 and 14, it is found that the influence of laser intensity fluctuation on fidelity is larger than that of working time fluctuation in general. In a word, our scheme is robust to dissipation caused by spontaneous emission, photon leakage, and the fluctuation of , , and T.

Fig. 13. In the coupled cavity system: (a) the fidelity of state transfer versus and δ T/T; (b) the fidelity of state transfer versus and δ T/T; (c) the fidelity of entangled state preparation versus and δ T/T; (d) the fidelity of entangled state preparation versus and δ T/T. The related parameters used for state transfer and entangled state preparation are the same as those used in Fig. 5.
Fig. 14. In the cavity–fiber–cavity system: (a) the fidelity of state transfer versus and δT/T; (b) the fidelity of state transfer versus and δ T/T; (c) the fidelity of entangled state preparation versus and δ T/T; (d) the fidelity of entangled state preparation versus and δ T/T. The related parameters used for state transfer and entangled state preparation are the same as those used in Fig. 9.
6. Conclusion

We proposed schemes of state transfer and entanglement preparation in coupled cavity system and cavity–fiber–cavity system respectively. The results of numerical simulations show that our schemes have high fidelity, greatly reduce the evolution time of the systems, and have high robustness for some dissipation and parameter fluctuations. We hope that our scheme can contribute to the processing of quantum information when it is widely used.

Reference
[1] Christandl M Datta N Dorlas T C Ekert A Kay A Landahl A J 2005 Phys. Rev. 71 032312
[2] Sillanpää M A Park J I Simmonds R W 2007 Nature 449 438
[3] Almeida G M A de Moura F A B F Lyra M L 2018 Phys. Lett. 382 1335
[4] Huang B H Kang Y H Chen Y H Shi Z C Song J Xia Y 2018 Phys. Rev. 97 012333
[5] Almeida G M A Ciccarello F Apollaro T J G Souza A M C 2016 Phys. Rev. 93 032310
[6] Man Z X An N B Xia Y J 2014 Ann. Phys. 349 209
[7] Kimble H J 2008 Nature 453 1023
[8] Li Y H Li X L Sang M H Nie Y Y Wang Z S 2013 Quantum Inf. Process. 12 3835
[9] Bennett C H Brassard G Crepeau C Jozsa R Peres A Wootters W K 1993 Phys. Rev. Lett. 70 1895
[10] Karlsson A Koashi M Imoto N 1999 Phys. Rev. 59 162
[11] Malaney R A 2010 Phys. Rev. 81 042319
[12] Hong C H Heo J Lim J I Yang H J 2014 Chin. Phys. 23 090309
[13] He X L Su Q P Zhang F Y Yang C P 2014 Quantum Inf. Process. 13 1381
[14] Deng Z J Feng M Gao K L 2007 Phys. Rev. 75 024302
[15] Clark S Peng A Gu M Parkins S 2003 Phys. Rev. Lett. 91 177901
[16] Zheng B Shen L T Chen M F 2016 Quantum Inf. Process. 15 2181
[17] Wu J L Su S L 2019 Europhys. Lett. 126 30001
[18] Wu J L Su S L 2019 J. Phys. A: Math. Theor. 52 335301
[19] Liu J X Ye J Y Yan L L Su S L Feng M 2020 J. Phys. 53 035503
[20] Teper N 2018 AIP Conf. Proc. 1936 020030
[21] Torres J P Deyanova Y Torner L Molina-Terriza G 2003 Phys. Rev. 67 052313
[22] Togan E Chu Y Trifonov A S Jiang L Maze J Childress L Dutt M V G Sorensen A S Hemmer P R Zibrov A S Lukin M D 2011 Nature 478 497
[23] Jin Z Su S L Zhang S 2019 Phys. Rev. 100 052332
[24] Heilmann R Grafe M Nolte S Szameit A 2015 Sci. Bull. 60 96
[25] Liu A P Cheng L Y Guo Q Su S L Wang H F Zhang S 2019 Chin. Phys. 28 020301
[26] Lemr K 2011 J. Phys. 44 195501
[27] Zhu X Y Liang E J Su S L 2019 J. Opt. Soc. Am. B. 36 1937
[28] Su S L 2018 Chin. Phys. 27 110304
[29] Su S L Liang E Zhang S Wen J J Sun L L Jin Z Zhu A D 2016 Phys. Rev. 93 012306
[30] Su S L Gao Y Liang E Zhang S 2017 Phys. Rev. 95 022319
[31] Su S L Tian Y Z Shen H Z Zang H Liang E Zhang S 2017 Phys. Rev. 96 042335
[32] Su S L Shen H Z Liang E Zhang S 2018 Phys. Rev. 98 032306
[33] Axline C Burkhart L Pfaff W Zhang M Chou K Campagne-Ibarcq P Reinhold P Frunzio L Girvin S M Jiang L Devoret M H Schoelkopf R J 2018 Nat. Phys. 14 705
[34] Bergmann K Theuer H Shore B W 1998 Rev. Mod. Phys. 70
[35] Lu M Xia Y Zhao L T Song J An N B 2014 Phys. Rev. 89 012326
[36] Muga J G Chen X Ibáñez S Lizuain I Ruschhaupt A 2010 J. Phys. 43 085509
[37] Chen Y H Xia Y Song J Chen Q Q 2015 Sci. Rep. 5 15616
[38] Song X K Ai Q Qiu J Deng F G 2016 Phys. Rev. 93 052324
[39] Masuda S Nakamura K 2011 Phys. Rev. 84 043434
[40] del Campo A Rams M M Zurek W H 2012 Phys. Rev. Lett. 109 115703
[41] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303
[42] Torrontegui E Lizuain I González-Resines S Tobalina A Ruschhaupt A Kosloff R Muga J G 2017 Phys. Rev. 96 022133
[43] Ibáñez S Martínez-Garaot S Chen X Torrontegui E Muga J G 2011 Phys. Rev. 84 023415
[44] Chen X Torrontegui E Muga J G 2011 Phys. Rev. 83 062116
[45] Du Y X Yue X X Liang Z T Li J Z Yan H Zhu S L 2017 Phys. Rev. 95 043608
[46] Lu M Zhang C L Zhang B Lin W S 2019 Laser Phys. Lett. 16 045206
[47] Tseng S Y. Wen R D Chiu Y F Chen X 2014 Opt. Express 22 18849
[48] Kiely A Benseny A Busch T Ruschhaupt A 2016 J. Phys. 49 215003
[49] Impens F Guéry-Odelin D 2017 Phys. Rev. 96 043609
[50] Shen C P Wu J L Su S L Liang E 2019 Opt. Lett. 44 2036
[51] Chen X Muga J G 2012 Phys. Rev. 86 033405
[52] Baksic A Ribeiro H Clerk A A 2016 Phys. Rev. Lett. 116 230503
[53] Kang Y H Chen Y H Shi Z C Song J Xia Y 2016 Phys. Rev. 94 052311
[54] Ban Y Jiang L X Li Y C Wang L J Chen X 2018 Opt. Express 26 31137
[55] Wu J L Ji X Zhang S 2017 Sci. Rep. 7 46255
[56] Wu J L Ji X Zhang S 2017 Quantum Inf. Process. 16 294
[57] Muga J G Chen X Ruschhaupt A Guéry-Odelin D 2009 J. Phys. 42 241001
[58] Kang Y H Chen Y H Wu Q C Huang B H Song J Xia Y 2016 Sci. Rep. 6 36737
[59] Schaff J F Song X L Capuzzi P Vignolo P Labeyrie G 2011 New J. Phys. 13 113017
[60] Wang Z Xia Y Chen Y H Song J 2016 Eur. Phys. J. 70 162
[61] Chen X Muga J G 2010 Phys. Rev. 82 053403
[62] Zhang J Li F G Xie Y Wu C W Ou B Q Wu W Chen P X 2018 Phys. Rev. 98 052323
[63] Chen Y H Xia Y Wu Q C Huang B H Song J 2016 Phys. Rev. 93 052109
[64] Wu J L Su S L Ji X Zhang S 2017 Ann. Phys. 386 34
[65] Martínez-Garaot S Torrontegui E Chen X Muga J G 2014 Phys. Rev. 89 053408
[66] Chen Y H Xia Y Chen Q Q Song J 2015 Phys. Rev. 91 012325
[67] Facchi P Marmo G Pascazio S 2009 J. Phys: Conf. Ser. 196 012017
[68] Shen L T Chen X Y Yang Z B Wu H Z Zheng S B 2011 Phys. Rev. 84 064302
[69] Vitanov N V Halfmann T Shore B W Bergmann K 2001 Ann. Rev. Phys. Chem. 52 763
[70] Vitanov N V Suominen K A Shore B W 1999 J. Phys. 32 4535
[71] Serafini A Mancini S Bose S 2006 Phys. Rev. Lett. 96 010503
[72] Kang Y H Chen Y H Shi Z C Huang B H Song J Xia Y 2017 Phys. Rev. 96 022304