† Corresponding author. E-mail:
Project supported by the Youth Program of the National Social Science Foundation of China (Grant No. 18CJY057).
It is generally accepted that herding behavior and overconfidence behavior are unrelated or even mutually exclusive. However, these behaviors can both lead to some similar market anomalies, such as excessive trading volume and volatility in the stock market. Due to the limitation of traditional time series analysis, we try to study whether there exists network relevance between the investor’s herding behavior and overconfidence behavior based on the complex network method. Since the investor’s herding behavior is based on market trends and overconfidence behavior is based on past performance, we convert the time series data of market trends into a market network and the time series data of the investor’s past judgments into an investor network. Then, we update these networks as new information arrives at the market and show the weighted in-degrees of the nodes in the market network and the investor network can represent the herding degree and the confidence degree of the investor, respectively. Using stock transaction data of Microsoft, US S&P 500 stock index, and China Hushen 300 stock index, we update the two networks and find that there exists a high similarity of network topological properties and a significant correlation of node parameter sequences between the market network and the investor network. Finally, we theoretically derive and conclude that the investor’s herding degree and confidence degree are highly related to each other when there is a clear market trend.
The study of complexity science has been a research hotspot in recent years, and complex networks and time series provide two theoretical ways to describe the complex system. As we gradually have a more in-depth understanding of the complex systems, we start to study time series from the perspective of network science, which not only riches the means of characterizing time series but alsoconduces to understanding the internal evolutionary mechanism of time series.[1]
Zhang et al. first pointed out that white noise sequences can be transferred into random networks which exhibit the small world and scale-free characteristics.[2] After that, different approaches have been put forward to studying the fundamental properties of time series in the view of complex networks. According to various definitions of network nodes and edges, current conversion methods can be roughly divided into phase space reconstruction,[3–7] visibility graph,[8–13] and probabilistic transfer method.[14,15] However, these methods only re-examine the time series on the surface, which lacks strong theoretical foundations as their support. Also, they do not retain time information in the network structure. To solve these problems, Zhao et al. presented a dynamically equivalent transformation method based on the coarse geometry theory and proved the equivalence property between complex networks and time series under the perspective of topological structure, geometrical characteristic, dynamic characteristic, and correlation dimension.[16]
In addition to the significant theoretical progress, complex networks have also been used to describe and characterize nonlinear systems in the real world, such as stock prices,[17] exchange rates,[18] traffic flows,[19] power,[20] social system,[21] macroeconomics,[22] etc. However, no one has studied the decision-making behavior of irrational investors in the stock market by using complex networks.
Herding behavior and overconfidence behavior are two kinds of irrational behaviors that kept attracting attention from academic researchers in behavioral finance in recent years. We can find the literature about the herding behavior in different investment bodies, the market conditions that may lead to herding, and the influence of herding behavior on financial markets. People tend to imitate others because they assume that others have information that can justify their actions. Sias found that institutional investors follow each other into and out of the same securities.[23] Barber et al. studied the trading of individual investors by using transaction data and documented the result that individual investors’ herd.[24] Gontis et al. suggested that human herding is so strong that it persists even when other evolving fluctuations perturb the financial system.[25] There is also some literature studying the conditions that lead to herding behavior. Kremer and Nautz showed that herding intensity of institutions depends on stock characteristics, including past returns and volatility.[26] Galariotis et al. found that US investors tend to herd during days when important macro data are released.[27] The influence of herding has also attracted much attention. Chiang and Zheng argued that crisis triggers herding activity in the crisis country of origin and then produces a contagion effect, which spreads the crisis to neighboring countries.[28] Bikhchandani and Sharma,[29] Gervais and Odean,[30] Park and Sabourian,[31] Blasco et al.[32] all held the view that herding generates more volatile prices.
Overconfidence is a psychological phenomenon that people overestimate the accuracy of their information and their investment analysis. Studies related to overconfidence behavior mainly focus on manifestations of overconfidence, the comparison of overconfidence extent among various groups, and the impact of overconfidence on financial markets. Hoelzl and Rustichini observed that people may be overconfident in many ways.[33] For example, they may perceive themselves more favorably than others, or they may perceive themselves more favorably than they perceive others. Benoît and Dubra found that it is common for most of people to rank themselves as better than the median.[34] Some studies focused on the performance differences among different investment groups. Barber and Odean proved that men trade more excessively than women.[35] Chuang and Susmel showed that individual investors are more confident than institutional investors.[36] Overconfidence behavior may play a role in excessive market volume and volatilities.[37–39]
Above all, as is well known, the herding investors tend not to value their private information, while the overconfident investors always overemphasize their own information. However, these two seemingly opposite behaviors can both lead to some common market phenomena, such as excessive trading volume and price volatility. Recent studies tended to examine herding behavior or overconfidence behavior alone. Because the traditional time series method mainly focuses on trends, fluctuations, and periodic characteristics of data, in this paper we try to explore whether there exist any network connections between these two kinds of behaviors based on the method of complex networks, which may provide us with a more comprehensive perspective to understand investors’ behaviors.
In this paper, we first introduce the improved mapping approach to transform a time series into a network, which is suitable for the transaction data in the stock market. Then, we briefly describe the financial background of stock market equilibrium. Next, we construct a static market network representing the market trends in the eyes of a representative investor and a static investor network reflecting the past performance of the investor. As the stock market equilibrium moves with the arrival of new information, we make rules for the evolution of complex networks. After that, we find that the weighted in-degrees of nodes in the market network and the investor network can represent the herding degree and the confidence degree of the investor, respectively. Using the transaction data of Microsoft, we present the images of the market network and the investor network before and after updating. Finally, we compare the network topological properties and the node parametric properties between the two networks, finding that there do exist correlations between them at the same moment. For further discussion, we theoretically derive the conditions for the convergence between the investor’s herding degree and confidence degree, that is, the coefficient of variation of price changes has to be low.
This paper has made the following three main contributions. Firstly, existing researches on investor behavior usually use traditional econometric methods[26,36] or simulations.[30,40] To the best of our knowledge, we are the first to analyze the behaviors of investors based on complex networks and conclude their evolution patterns, which cannot be obtained by the traditional methods. Secondly, the common mapping method is to convert an unchangeable time series into a static network or do comparative static analysis of multiple networks in chronological order. We design the rules that allow networks to evolve dynamically with the update of time series. Finally, existing researches on market anomalies are single and isolated. When it comes to herding behavior and overconfidence behavior, no one has theoretically or empirically studied their possible connections. Some people tend to believe that they are mutually exclusive due to their seemingly contradictory definitions. To fill this void in the literature, we transform time series to networks and find a high similarity for the indicators of network betweenness centralization, network clustering degree and modularity and significant correlations for the node parameter sequences of weighted in-degree, weighted out-degree and weighted degree between the market network which is the basis of the investor’s herding behavior and the investor network which is the foundation of the investor’s overconfidence behavior. Moreover, we derive and obtain the convergence conditions of the herding degree and confidence degree of the investor.
The remainder of the paper is organized as follows. In Section
The key to studying time series from the perspective of complex network theory is to choose an effective conversion method. As mentioned before, Zhao et al. presented a practical transformation approach between time series and complex networks based on the amplitude difference of data points.[16] Let {pt |t = 1,2,…,N} be a scalar time series of N observations and ε be a threshold. The adjacency matrix of the transformed network is defined as A = {ast |s = 1,2,…,N; t = 1,2,…,N}, where ast = 1 if |ps − pt| < ε, otherwise ast = 0. That is, there exists a link from node s to node t if the distance between the nodes is less than the threshold. The basis of the equivalence theorem of dual characterization between time series and complex networks is the topological homeomorphism theorem and quasi-isometric theorem. They found that the waveform of the reconstructed time series and the original time series are exactly the same, which means that this conversion method implements an equivalently mathematical description of time series under network representation.
Suppose that there is only one financial asset in the stock market. The market consists of I heterogeneous active traders who take long position or short position in this security. The movement from the (t − 1)-th to the t-th Walrasian equilibrium is driven due to the arrival of new information. Let Pt denote the current market price, and Pti the i-th trader’s reservation price which is his belief about the stock price in the future at time t, where i = 1,2,…,I. Assume that there are no transaction costs and the I traders differ only in their beliefs (Since different traders only differ in their beliefs, we only study the investment behavior of the i-th active trader for convenience), then the inter-trader differences in their beliefs will arise from different expectations about the future and from different needs to transfer risk through the market.
Consequently, all price risk is viewed as falling on terminal wealth. The agent is assumed to choose position Qti to maximize the expected utility of terminal wealth. The gain attributable to this speculative position and hence its contribution to terminal wealth is


Equilibrium requires 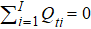

Now, we consider the movement from the (t − 1)-th to the t-th equilibrium. A piece of news arrives at the market and changes the individuals’ reservation prices. Since in equilibrium, the total number of buy orders matches the total number of sell orders, we have
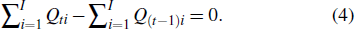
The resulting change in the market price is the weighted average of the increments with respect to the traders’ reservation prices, which implies
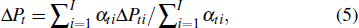
We have introduced the decision-making behavior of rational investors above, where market prices and investor’s reservation prices are both exogenous. However, we know that investors cannot be rational all the time in real life, so their investment decisions may be affected by their sentiment. For example, if the market trend is particularly apparent, the trader will be sure of his belief, and hence increasing his positions. That is what we see as the “buying the winners” strategy. Moreover, a trader will become more optimistic when he tends to judge correctly for the market price changes recently or after a high level of return,[42] which will lead to excessive transactions.
We can see that investors’ seemingly opposite behaviors, such as following others and believing in themselves, can both lead their desired positions to increase. This raises the question whether an investor can behave both herding and confidence at the same time. If so, does any connection exist between them? Moreover, what is their combined effect on the investor’s position? To answer these questions, we construct a market network that represents the market trend and an investor network that represents the past judgments from the perspective of a representative investor in the following subsection.
Following the work of Zhao et al.,[16] we will build complex networks based on the time series of price changes (Due to the relatively large fluctuations in the time series of stock prices, which will interfere with the study of statistical properties of the data, used in this paper are the differenced stock prices, that is, the time series of price changes) and past judgments for the representative i-th investor.
Firstly, in the market network, we define node t as the market price change at time t and the edge from node (t − m) to node t as the influence of the market price change at time (t − m) on the market price change at time t. Considering that the current market price change cannot have an influence on the past market price changes, and the memory length of the trader is limited (assuming the i-th investor’s memory length is M) (Although each one observes the same market prices, their herding behavior may be different due to the various memory lengths), we give definitions below.
Similarly, we can construct an investor network based on the past judgments of the i-th investor.
Every time when a piece of new information arrives at the market, each trader will update his reservation price and then obtain the market clearing price. If the directions of the two price changes are the same, the trader will make the right investment decision because his judgment is consistent with the judgment of the majority. Therefore, for the investor network, we employ node t to represent the product of the market price change and the trader’s reservation price change at time t and the edge from node (t − m) to node t to represent the effect of the trader’s judgment at time (t − m) on the judgment at time t. Being the same as the market network, the trader’s current judgment cannot influence the past judgment, and the memory lengths of different traders are different (assuming that the i-th investor’s memory length is M), we give another definition below.
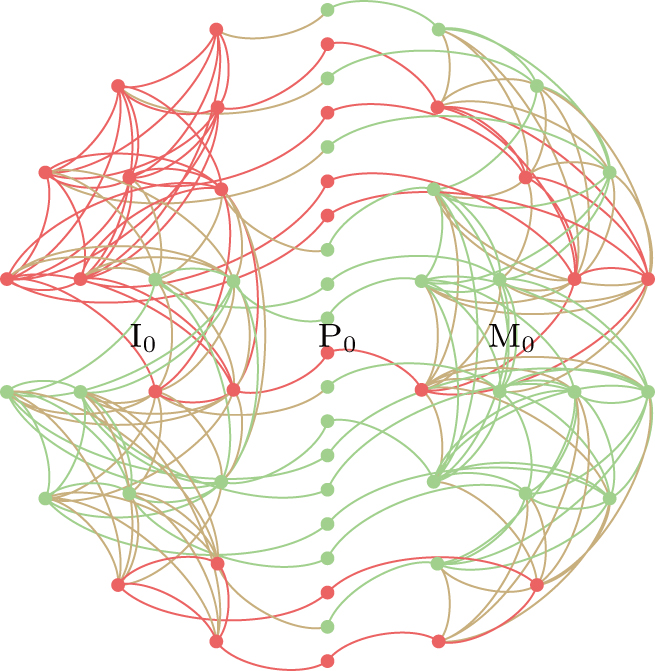
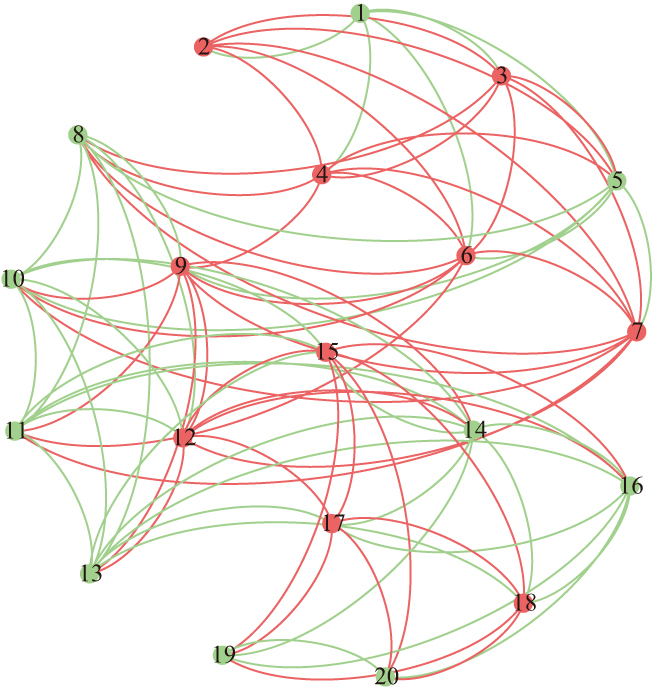
To have an intuitive understanding of the mapping from time series to complex networks, we present the network structures of the stock price series (P0), the price change series and the investor judgment series together based on the sample of Microsoft’s stock prices during the first 20 trading days in July 2009. Specifically, we transfer the price change series into the market network (M0) according to Definition
In this section, we will first describe how the market network and the investor network evolve with the change of recent market fluctuation and the trader’s past performance, respectively. Also, we will intuitively present the evolution patterns of these networks to have a more in-depth understanding of the changing process.
The networks constantly evolve as the stock market moves from one equilibrium to the next one. Due to the similar structure between the market network and the investor network, we take the market network for example to explain the dynamic evolution of the network structure in detail.
It is supposed that there are always N nodes in chronological order of a network. When a piece of news arrives at the stock market, we obtain a new market clearing price, thus a new market price change. At this time, we add a new node to this network and meanwhile delete the first node of the network, so there are still N nodes. Since the memory of investors is limited, we assume that only the previous M nodes can affect the t-th node in the eyes of investors. That is, there will be M directed edges from the previous M nodes to the new t-th node. Then, how is the influence of former nodes on the t-th node judged?
Assuming that every time when a node k is added to the network, the investor will compare the size of the k-th node ΔPk with the sizes of the previous M nodes ΔPk − 1, ΔPk − 2, …, ΔPk − M. If the difference between ΔPk and ΔPk − m is smallest, then xk = m, where x is defined as a discrete variable taken on values 1, 2, 舰, M. This means that the (k − m)-th node has the most significant influence on the k-th node. In other words, the status of node k is more likely to be transformed from the status of node (k − m) than the other previous M nodes. Let k traverse from (t − N) to (t − 1), then 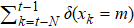
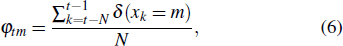
Meanwhile, the i-th investor compares the size of the k-th node ΔPk ΔPki with the sizes of the previous M nodes ΔPk − 1 ΔP(k − 1)i, ΔPk − 2 ΔP(k − 2)i, …, ΔPk − M ΔP(k − M)i in the investor network. If the difference between ΔPk ΔPki and ΔPk − m ΔP(k − m)i is smallest, then yk = m, where y is defined as a discrete variable taken on values 1, 2, …, M. Therefore, the transition probability from the the (t − m)-th node to the t-th node in the investor network can be expressed as
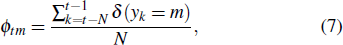
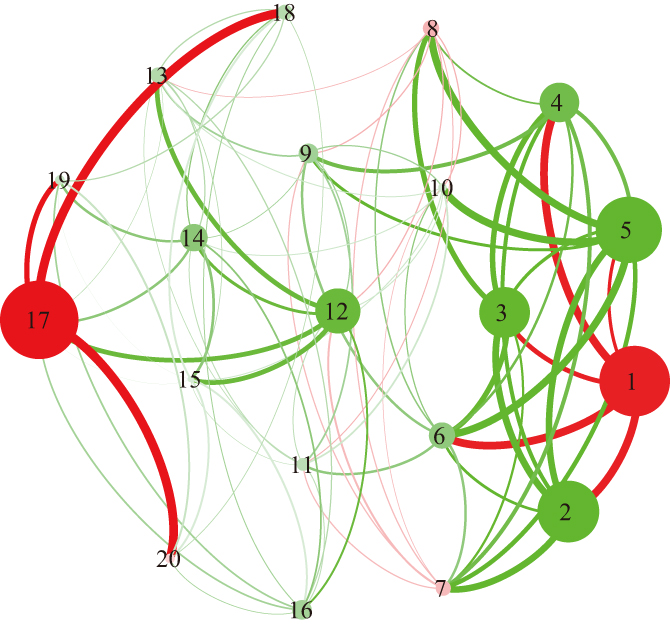
The weighted degree is a critical statistical index in the complex network. The higher the weighted in-degree or out-degree of the node, the more critical the node is in the complex network.[43] We explore the economic implications of weighted in-degree of the market network in this subsection and weighted in-degree of the investor network in the next subsection.
Based on the dynamic evolution process described above, the weighted in-degree of node t in the market network can be expressed as the sum of the influence of nodes which have direct links to node t on node t, that is,

We can see from Eq. (
Considering the consistency between the size of the weighted in-degree and the investor’s herding degree with the change of market trend, we can use the absolute value of the weighted in-degree to indicate the investor’s herding extent, that is,
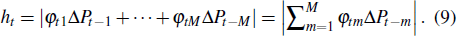
At the beginning of each period t, the i-th trader forms his herding degree based on the past market trend. The higher the absolute value of the weighted in-degree, the stronger the investor’s herding degree will be.
To clearly show the changes of the market network before and after being updated, we construct the market network by using the Microsoft’s transaction data spanning from July 1, 2009 to June 30, 2019 which consists of 2517 observations. Suppose that there are always 20 nodes in a static network, i.e., N = 20, and the memory length of a typical investor is one week, that is, M = 5, then we will update the network by using the method described above. Figure
Similarly, we can express the weighted in-degree of node t in the investor network as
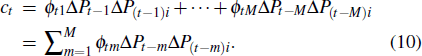
If the i-th investor judges correctly at time (t − m), then Δpt − m Δp(t − m)i > 0, otherwise Δpt − m Δp(t − m)i ⩽ 0. The weighted in-degree will increase with the right extent of judgment increasing and decrease with the wrong extent of judgment increasing. Meanwhile, the confidence extent of investors also has a similar change pattern to the weighted in-degree in the investor network. Odean argued that investors’ degree of overconfidence can be measured by their early excess net return.[37] Many researchers believed that in the stock market, most of investors tended to take too much credit for the excess profits they had obtained, which would produce more trading and volatility.[30,36,46] In a word, the key to overconfidence is that investors have made the correct judgments many times, and they believe that it is their own abilities that help them make the right judgments. Therefore, we can use the value of the weighted in-degree in the investor network to indicate the confidence extent of investors. At the beginning of each period t, the i-th trader forms his confidence extent based on past judgments. The higher the weighted in-degree, the stronger the investor’s confidence degree will be.
We still use Microsoft’s stock prices to calculate market price changes. However, the data of the traders’ reservation prices are not available, so we simulate the i-th trader’s reservation prices as follows:
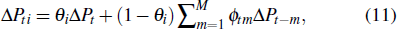
To explore the potential correlations between the market network and the investor network, we will analyze the properties of the two networks at the network level and the node level in this section.
The common practice of comparing two networks at network level is to compare some main topological indicators, including the network betweenness centralization, network clustering coefficient, and modularity degree.
To verify the generality of the experimental results, apart from employing Microsoft’s transaction data spanning from July 1, 2009 to June 30, 2019 in the previous article, we present the corresponding results of Microsoft’s transaction data from July 1, 2009, respectively, to September 30, 2015, December 31, 2016, and March 31, 2018. We choose different months as the cut-off time so as to exclude the interference of quarterly effects in the stock market. Also, we show the network topological indexes and the correlation coefficients between the node parameter sequences based on the data of the US S&P 500 stock index and the China Hushen 300 stock index. We use M0 and I0 to denote the market network and the investor network before being updated, M1 and I1 to represent the two networks after being updated. The results are shown in Table
| Table 1. Network topological indexes. . |
Network betweenness centralization is the average of the ratios of the number of paths that pass through each node to the total number of shortest paths, which can be used to measure the average bridge intermediation of network nodes. Table
Network clustering coefficient is a measure of the degree to which the nodes in a graph tend to cluster together. We can see from Table
Modularity is used to measure the strength of the division of a network into modules that are also called groups, clusters, or communities. Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. From Table
In this part, we focus on the parameters related to the nodes such as the weighted in-degree, weighted out-degree, and weighted degree (The weighted in-degree in the market network is taken as its absolute value in the following calculation due to its significant economic meaning discussed in Subsection
Weighted in-degree is the sum of the weights of the edges entering a node.
Weighted out-degree is the sum of the weights of the edges leaving a vertex.
Weighted degree is the sum of weighted in-degree and weighted out-degree.
Using the updated networks, we first compute the corresponding parameters of each node. Then, we obtain two parameters series, and thus we can calculate their correlation coefficients. To confirm that the correlation coefficient is only significant between the two networks at the same time, we also calculate the correlation coefficients between the updated market network (M1) and the investor network before being updated (I0), and the updated investor network (I1) and the market network before being updated (M0) for each node parameter. The results are shown in Table
| Table 2. Correlation coefficients for node parameter sequences. . |
From Table
As demonstrated in Section


We finish this section by analyzing the internal mechanisms behind our conclusions. We suggest that these two kinds of behaviors that seem to be mutually contradictory are in fact consistent when their variations with the mean of the price changing are low. In particular, when their variations with the market price changing is small, which means that the market price changes are stationary, the market will show a clear trend. According to Eq. (
However, when the coefficient of variation is large, investors do not have the chance to follow the crowd. At this time, whether investors have made their right judgments is entirely accidental, so a trader’s herding degree is almost not correlated with his confidence degree. For example, if the price of a stock goes up and down like a seesaw for some time, then investors will not have any trends to follow. At this time, some investors will increase their positions, and others will reduce their positions. The irregular behaviors of investors will have an uncertain influence on the direction of price change, so investors cannot continuously obtain positive returns, and their confidence degrees cannot accumulate.
Since it is difficult to study the relationship between investors’ herding behavior and overconfidence behavior by using traditional approaches, in this paper we propose a framework to study the mechanism between herding behavior and overconfidence behavior from the perspective of the complex network. In this framework, we transform a time series into a complex network based on the amplitude difference of data points. The nodes represent the market price change in the market network and the investor’s past performance in the investor network, respectively. The stock market moves from one equilibrium to another with time, so we characterize the transition probability with the transition frequency of node status in the past, and then present the dynamic evolution processes of the two networks. Since the investor’s herding degree depends on the market trend and the investor’s confidence degree depends on his past performance, we use the weighted in-degrees of the nodes in the market network and those in the investor network to represent the investor’s herding degree and confidence degree, respectively. To reflect the change of the investor’s herding degree and confidence degree with the arrival of new information, we design the rules that the network can evolve dynamically as new information reaches the market. Finally, we find that the market network and the investor network at the same point are not only highly similar in the topological nature, but also their node parameter sequences have a certain correlation. Due to the economic significance of the weighted in-degree, we focus on it and find that an investor’s herding degree is highly related to his confidence degree if there exists a clear market trend.
Our conclusions provide the support for explaining the price-volume relation. Karpoff reviewed previous empirical and theoretical research and proposed a model that further verifies the positive correlation between volume and the absolute value of the price change or the price change per se in stock markets.[47] As we introduced in Section
Our findings also have some policy implications. Firstly, the investment decisions made by investors are inevitably affected by the global market environment, such as market price changing over a period of time. When the market conditions are good, investors should realize that the seemingly favorable market environment may be a kind of “illusion”, that is, the result of malicious manipulation by investors with dominant capital. Otherwise, uninformed investors would believe that they have seized the market trend, thereby accumulating the excessive confidence in a short time. It may cause huge losses when market manipulators decide to harvest. Secondly, regulators should establish a perfect investor protection mechanism. Both professional investment institutions and individual investors should receive educations on securities law and risk warning. It is also necessary to popularize the investment techniques and investment strategies and encourage investors to learn psychological knowledge. In other words, regulators should guide investors in avoiding short-term overconfidence and establishing a sense of rational investment.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |