Cite this Article
Hao Jia-Zheng, Hu Feng-Xia, Yu Zi-Bing, Shen Fei-Ran, Zhou Hou-Bo, Gao Yi-Hong, Qiao Kai-Ming, Li Jia, Zhang Cheng, Liang Wen-Hui, Wang Jing, He Jun, Sun Ji-Rong, Shen Bao-Gen. Multicaloric and coupled-caloric effects. Chinese Physics B, 2020, 29(4): 047504  
Permissions
Multicaloric and coupled-caloric effects
Hao Jia-Zheng1, 2, Hu Feng-Xia2, 3, 4, †, Yu Zi-Bing2, 3, Shen Fei-Ran2, 3, Zhou Hou-Bo2, 3, Gao Yi-Hong2, 3, Qiao Kai-Ming2, 3, Li Jia2, 3, Zhang Cheng2, 3, Liang Wen-Hui2, 3, Wang Jing2, 3, 5, He Jun1, ‡, Sun Ji-Rong2, 3, 4, Shen Bao-Gen2, 3, 4
Division of Functional Material Research, Central Iron and Steel Research Institute, Beijing 100081, China
Beijing National Laboratory for Condensed Matter Physics & State Key Laboratory of Magnetism, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
Songshan Lake Materials Laboratory, Dongguan 523808, China
Fujian Innovation Academy, Chinese Academy of Sciences, Fuzhou 350108, China

 

† Corresponding author. E-mail: fxhu@iphy.ac.cn hejun@cisri.com.cn

Project supported by the National Key Research and Development Program of China (Grant Nos. 2017YFB0702702, 2019YFA0704904, 2018YFA0305704, 2017YFA0206300, 2017YFA0303601, and 2016YFB0700903), the National Natural Science Foundation of China (Grant Nos. U1832219, 51531008, 51771223, 51590880, 51971240, 11674378, 11934016, and 11921004), and the Key Program and Strategic Priority Research Program (B) of the Chinese Academy of Sciences.

Abstract

The multicaloric effect refers to the thermal response of a solid material driven by simultaneous or sequential application of more than one type of external field. For practical applications, the multicaloric effect is a potentially interesting strategy to improve the efficiency of refrigeration devices. Here, the state of the art in multi-field driven multicaloric effect is reviewed. The phenomenology and fundamental thermodynamics of the multicaloric effect are well established. A number of theoretical and experimental research approaches are covered. At present, the theoretical understanding of the multicaloric effect is thorough. However, due to the limitation of the current experimental technology, the experimental approach is still in progress. All these researches indicated that the thermal response and effective reversibility of multiferroic materials can be improved through multicaloric cycles to overcome the inherent limitations of the physical mechanisms behind single-field-induced caloric effects. Finally, the viewpoint of further developments is presented.

PACS: ;05.70.Fh;;65.40.gd;;75.30.Sg;;75.85.+t;
Keyword:;multicaloric effect;;coupled-caloric effect;;solid-state refrigeration;;magnetocaloric effect;
1. Introduction

Solid-state refrigeration technology based on the caloric effects has superior refrigeration efficiency while reducing ozone consumption or greenhouse gas emissions. Therefore, it provides an energy-saving and environmentally-friendly refrigeration solution to replace the current mainstream vapor compression refrigeration technology.[1–6] The caloric effect of a solid refers to the reversible thermal change (isothermal change of entropy or adiabatic change of temperature) of the solid under the application of an external stimulus field, which generally occurs in the vicinity of phase transitions. The known caloric effects mainly include magnetocaloric effects,[1–6] electrocaloric effects,[7] and mechanical caloric effects (barocaloric[8] and elastocaloric effects[9]), which correspond to magnetic, electric, and mechanical fields (hydrostatic pressure and uniaxial stress), respectively. Multiferroic materials show two or more ferroic orders, and when the couplings of these ferroic orders are strong enough, each ferroic order can respond to more than one type of applied field. In addition, multiple ferroic phase transitions may occur at a nearby temperature. Therefore, it is expected that most giant magnetocaloric and electrocaloric materials will also exhibit mechanocaloric effects, since the magnetic and polar orders in such materials are strongly coupled to the lattice order.[10] The magnetocaloric, electrocaloric, or mechanocaloric effect will directly affect each other due to the cross-response to the magnetic/electric or mechanical field. Some studies have shown that the multicaloric effect driven by multiple fields may yield larger caloric response compared to the caloric effect induced by a single stimulus.[11–17]

So far, the study of single-field induced solid-state caloric effects has attracted widespread attention. In particular, giant magnetocaloric effects are generally observed when the ferroic phase transition is first order in nature.[18–27] Many studies have focused on achieving stronger magnetic first-order transitions, that is, achieving the greatest latent heat and the strongest magnetic–structural coupling. This method is beneficial to achieve higher caloric performance, especially large entropy changes. However, it is accompanied by many disadvantages, such as large hysteresis loss, irreversibility of caloric effects, or poor mechanical stability. These definite drawbacks have limited the practical application and further development of the first-order transition materials in solid-state refrigeration. Considerable efforts have recently been made to overcome these problems.[28–34] Recent studies indicated that the hysteresis loss of materials can be reduced or even eliminated by utilizing the response of multiferroic materials to more than one type of driving field.[29,30,32] These studies have led to an enthusiastic search for multicaloric cycle and have encouraged fast-growing research activities in the field. The theoretical framework for multicaloric effect has been studied in sufficient detail.[16,17,35–37] However, due to the limitation of the current experimental technology, quite few experimental efforts have been devoted to the study of these combined magneto–mechanic or electro–mechanic caloric effects with the coupled term considered.[15,17,38] At present, most of the reported results involve studies on the effects of mechanical stress on the magnetocaloric and electrocaloric effects, while a small amount focus on the regulation of electro-induced strain on the magnetocaloric effect in magnetostructural coupled materials. Furthermore, cryogenic rare earth-based alloys and intermetallic compounds are mainly second order materials showing considerable magnetocaloric effect (MCE),[4,5,39–44] such as R–T (R = rare earth element; T = Fe, Co, Ni, Zn, and Ga) compounds,[5,45–54] ternary RTX (T = Fe, Co, and Pt; X = Al, Mg, and C) compounds,[55–60] ternary R2T2Al (T = Co, Ni, and Cu) and R2Ni2In compounds,[41,61,62] ternary R4TX (T = Co, Pd, and Pt; X = Mg and Cd) compounds,[63,64] and quaternary RNi2B2C and RNiBC compounds.[65] However, some of these rare earth-based MCE materials still undergo unneglectable spin–lattice coupling, though the thermal and magnetic hysteresis may be approaching zero. For example, the spin orientation transition is occasionally accompanied by an abnormal lattice change, and a stress can also shift the transition. Because the experimental studies on the multicaloric and coupled-caloric effects are still limited, there are no relative reports involving the rare earth-based MCE materials up to now. Therefore, in this article the review mainly focuses on the multicaloric effect and coupled-caloric effect in the materials with significant characteristics of first-order transition.

In this article, we present a brief review of the state of the art in research on multicaloric materials and multicaloric effects. The phenomenology and fundamental thermodynamics of the multicaloric effect are reviewed, including some common theoretical and experimental approaches to study the multicaloric effect and coupled-caloric effect. Finally, the viewpoint of further developments is presented.

2. Thermodynamics of multicaloric effect

The ferroic material can be characterized by ferroic property Xi. with corresponding thermodynamically conjugated field xi. These pairs of variables can be magnetization M and magnetic field H, polarization P and electric field E, or strain ε and stress σ. The caloric effects caused by the finite changes in the field xi (keeping the remaining fields constant) are usually quantified by the entropy changes that occur when the field is applied or removed isothermally, and the temperature changes that occur when the field undergoes an adiabatic change. The isothermal change of the field-induced entropy can be obtained by integrating the appropriate Maxwell equation[15,17,36,37]

When the field is varied adiabatically, the entropy is constant. The adiabatic temperature change can be obtained by the following equation:

Multiferroic materials display two or more of the non-independence ferroic properties, and they may be strongly coupled. The multicaloric effects occur when more than one field is either simultaneously or sequentially applied. For the sake of clarity and practical applications, the system is considered with two ferroic properties X1 and X2 with thermodynamically conjugated fields x1 and x2, respectively. In general, for adiabatic temperature changes, it is easy to obtain similar expressions to that obtained for isothermal entropy changes. Similar to the caloric effect induced by a single field in an equilibrium thermodynamic system, the multicaloric effect can also be quantified by the isothermal entropy change. Furthermore, the entropy is a state function, so the magnitude of the isothermal entropy change is independent of the thermodynamic path of the applied multiple external fields, and it does not depend on whether the driving fields are applied simultaneously or sequentially. Assuming the system responds isotropically to the applied field, the change in entropy caused by the isothermal change in the two fields can be expressed as[15,17,36,37]

The first term on the right is only a single field-induced entropy change that quantifies the caloric effect related to the ferroic property X1

while the second term on the right is the caloric effect due to the application of field x2 at constant x1, and it can be written as the sum of terms of the single caloric effect associated with the induced change of the property X2 and a caloric cross-response contribution

where χ12 = (∂X1/∂ x2)T,x1 = (∂ X2/∂ x1)T,x2 is the cross-susceptibility that quantifies the response of X1 (X2) to the nonconjugated field x2 (x1). It indicates the strength of the interaction between ferroic properties X1 and X2. Therefore, due to the interaction between ferroic properties X1 and X2, the multicaloric effect is not a simple sum of the caloric effects associated with each one alone. The isothermal entropy change of the multicaloric effect can be written as

where the last coupled term produces the coupled-caloric effect.

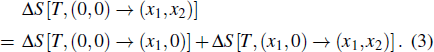
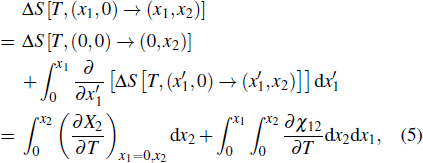
Another useful method for proving the interdependence of thermal response on different external fields is to analyze the caloric effects caused by changes in the ferroic property Xi on the application or removal of the non-conjugated field xj, and maintain the remaining fields constant. The ferroic property can be expressed as Xi = Xi (T, x1, x2), where i = 1, 2. One may then express the entropy change by the appropriate Maxwell relations as follows:[15,17,36,37]

where X1(0) and X1(x2) are the values of the X1 variable at x2 = 0 and at a given value of the field x2, respectively. Taking into account that

and , from Eqs. (6)–(8), the entropy change ΔS[T,x1 = 0,X1(0) → X1(x2)] can be expressed as

3. Theoretical approaches
3.1. First-principles calculations

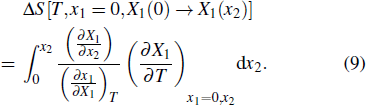
First-principles calculation plays a very fruitful role in the theoretical understanding of the multicaloric effect. Lisenkov et al. used first-principles simulations to study the multicaloric effect in a typical ferroelastic/ferroelectric PbTiO3, providing insights into the multicaloric effect of the material.[16] To explore the multicaloric nature of PbTiO3, they used the direct approach[66,67] to calculate the caloric change directly. The total energy of PbTiO3 is given by the effective Hamiltonian by the first-principles calculation. This Hamiltonian correctly predicts various structural and thermodynamic properties of PbTiO3, including polarization, Curie temperature, and some others. In addition, the total energy given by the Hamiltonian was used in the framework of an isenthalpic Monte Carlo simulation, which simulates the electrocaloric effect induced by a single electric field, the barocaloric effect induced by a single stress field, and the multicaloric effect induced by the electric field and pressure simultaneously. Their work found that the multicaloric effect far exceeds either piezocaloric or electrocaloric effect in the same material. In addition, when multiple external fields are applied, the strong coupling between the two ferroic order parameters plays a key role in the significant enhancement of the caloric effect. This study clearly shows that first-principles calculations are of great significance for understanding the multicaloric effect from a theoretical perspective.

3.2. Landau theory

The Landau model can also be used to describe the multiple thermal properties near phase transitions in the system. This model combines the coupling between the ordered parameters related to two ferroic properties. Planes et al. discussed the multicaloric effect under the combined action of a magnetic field and an electric field based on a system with a magnetoelectric coupling.[37,68] The related order parameters are the magnetization M and the polarization P. Therefore, the proposed Landau free energy contains pure terms related to the polar and magnetic contributions and terms that explain their interaction. That is, the free energy can be expressed as

In the Laudau phase transition theory, the following free energy contributions can be obtained:

where κ represents the magnetoelectric coefficient. Furthermore, according to the Curie–Weiss law,

where and are the paraelectric transition temperature and paramagnetic Curie temperature, respectively.

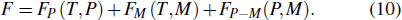
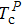
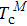
They assumed b > 0, β > 0, and γ > 0 to ensure that the pure ferroelectric and ferromagnetic free energy functions are positive definitely for large values of P and M. Electric field E and magnetic field H can be introduced by introducing Gibbs-like polar and magnetic free energies

The minimum of the Gibbs free energy G = GP + GM + FP − M relative to P gives the relationship between P and M,

When the applied electric field is zero, the following relationship exists in the ferroelectric phase:

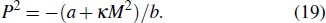
Therefore, the effective magnetic Gibbs free energy can be expressed as

with

From the Landau phase transition theory, the sign of the fourth-order coefficient B(κ) predicts that the magnetoelectric phase transition might be continuous or discontinuous. According to the above model, Plane et al. established a phase diagram of the magnetoelectric coupling coefficient and temperature, and pointed out that the slope of the coexistence line in the E–H diagram at a given temperature can be given by the generalized Clausius–Clapeyron equation in a first-order phase transition material

The pure electrocaloric effect can be obtained by the following equation:

where S0(T) = a(T)/(2b) and P2(T,E) is a solution of ∂ GP/∂ P = 0. In addition, at constant temperature, (∂ P/∂ T)E d E = − ηP P d P.

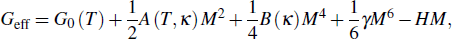
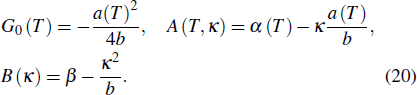
Furthermore, the isothermal entropy change induced by the magnetic field H can be expressed as the sum of the polar and magnetic contributions

where the cross-caloric term associated with the polar induced by the magnetic field is given by

and the pure magnetic contribution is given by

Therefore, the isothermal entropy change of the multicaloric effect induced by the simultaneous application of magnetic and electric fields can be obtained as

where

in this case, the relationship between P and M can be given by Eq. (19), and M(H,E) is the solution of ∂ Geff/∂ M = ∂ Feff/∂ M − H = 0.

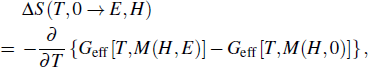
Plane et al. used these expressions to investigate the multicaloric effect within Landau theory.[36,37] The authors found that the application of both magnetic and electric fields can improve the whole effect when both the magnetic and polar contributions are conventional. In other words, when the signs of the entropy change of caloric effect induced by the magnetic field and the electric field are opposite, the magnitude of the multicaloric effect will be lower than that of the caloric effect induced by a certain single field.[36] They also analyzed the multicaloric effect in the magnetostructural metamagnetic shape-memory materials with a Landau model. Their phenomenological Landau results combined with first-principle calculations provide a route for designing materials with improved multicaloric effects.[37] Furthermore, several authors have studied the ferroelastic/ferroelectric single crystals within this framework.[35,69] Liu et al. reported the multicaloric effect in BaTiO3 single crystals driven simultaneously by mechanical and electric fields, which was described via the Landau free-energy model. They found that the multicaloric behavior is mainly dominated by the mechanical field rather than the electric field, since the paraelectric-to-ferroelectric transition is more sensitive to the mechanical field than to the electric field.[35] Meng et al. used a phenomenological calculation based on the Landau phase transition theory to evaluate the magnitude of the coupled-caloric effect in a ferromagnetic–ferroelectric system. Their results indicated that the magneto-electric coupling greatly strengthens the magnetization, ferroelectric polarization, and isothermal entropy change in the coupled ferromagnetic-ferroelectric multiferroic system. The caloric effect in the coupled system is greatly enhanced by increasing the magneto-electric coupling strength.[69]

3.3. Mean field model

To describe the muticaloric effect of specific materials in more detail, a reliable approach is to consider the mean field model which captures the internal mechanism expected to be more important. Stern-Taulats et al. used the mean field model for the free energy of the FeRh bulk to describe the antiferromagnetic (AFM) to ferromagnetic (FM) phase transition.[17] The model includes a magnetovolumic coupling term to account for the changes in unit cell volume during transition, and the coupling term includes the effect of external fields such as pressure P and magnetic field H. The total free energy of the system is f = fmag + fcoupling, and the variational Gibbs energy function per magnetic atom is

where mFe and mRh are the order parameters that describe the ferromagnetism of the sublattices of Fe and Rh; ηFe is the AFM order parameter of Fe; ω is the relative volume change; α1 and α2 are the magnetostriction coefficients, and α0 is the inverse of the compressibility. J is an effective exchange interaction parameter and z refers to the coordination number of the first neighbors.

Therefore, the entropy S of the system can be directly computed from Eq. (27) by employing the thermodynamic definition of S,

where mFe(T,H,P), mRh(T,H,P), and ηFe(T,H,P) are the equilibrium order parameters. The isothermal entropy change for the multicaloric effect induced by the application of pressure and magnetic field can be calculated from

Stern-Taulats et al. also studied the multicaloric effect and the effects of hysteresis within this mean field approximation and the model also nicely reproduced the experimental data of the magnetostructural coupled system (bulk FeRh) over a broad range of pressure, magnetic field, and temperature.[17]

4. Experiment approaches

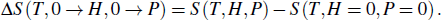
Previous theoretical studies have shown that the huge thermal response of a multiferroic material to an applied magnetic/electric field or stress originates from the strong coupling interaction between spin/polar and lattice. Due to the cross-response to mechanical, magnetic or electric fields, it is expected that the multicaloric effect driven by multiple fields can enhance the caloric effect and overcome some shortcomings such as the limitation of the cooling temperature window and irreversibilities due to hysteresis. However, most of previous experimental studies focused on the effect of hydrostatic pressure on the magnetocaloric effect and the electrocaloric effect. Hydrostatic pressure, as a clean means compared to chemical pressure, has been successfully used to tune the temperature position through impacting the magnetostructural/magnetoelastic transition for the giant MCE materials. However, the magnitude of MCE could be seldom enhanced by a physical pressure except for a few cases where the enhanced MCE mainly originates from the enhanced contribution of the lattice and the strengthening of the first-order transition by the pressure.[11–13] For example, the application of hydrostatic pressure on Tb5Si2Ge2 compound[11] can significantly enhance the MCE by changing the phase transition from second-order to first-order in nature. Large enhancements of magnetocaloric and barocaloric effects by hydrostatic pressure were also observed in La(Fe0.92Co0.08)11.9Si1.1 compound,[12] which mainly originate from the increased contribution of the lattice entropy change (ΔSLatt). Neutron powder diffraction revealed that the hydrostatic pressure sharpens the magnetoelastic transition and enlarges the volume change, ΔV/V, during the magnetoelastic transition through altering the specific atomic environments of NaZn13-type structure.[12] For the Ni2In-type hexagonal (MnNiSi)1 − x(MnFeGe)x alloys, enhanced MCE by hydrostatic pressure was also observed, which was ascribed to the enlarged ΔV/V across the magnetostructural transition.[13] The estimated enhancement of ΔV/V is up to 7% by pressure according to the relation between the ΔSLatt and volume change ΔV/V, i.e., δ[ΔV/V(%)]/δ(ΔSLatt) = 0.08 J · kg−1 · K−1.

Moreover, for the MCE materials with magnetostructural/magnetoelastic transition, the inherent hysteresis loss can be reduced through dual-field regulation or multicaloric cycle. For example, a reduction of magnetic hysteresis has been observed in Ni–Mn–In–Co bulk, where the sample is magnetized at ambient pressure while demagnetized under 1.3 kbar.[29] FeRh alloys have also been studied from this perspective. Liu et al. reduced the magnetic hysteresis loss by 96% in a dual-field magneric-electric refrigeration cycle for FeRh/BaTiO3 heterostructures.[30] The multicaloric cycle gives rise to larger reversible caloric effect than any single field. The same situation was demonstrated in the multicaloric cycle of FeRh/PMN-PT heterostructure.[32] Qiao et al. reported a nonvolatile reduction of hysteresis loss in FeRh film, and quantitative analysis indicated that the effective refrigeration capacity (RCeff) can be increased to a new height by utilizing the external mechanical work as long as the nonvolatile strain can be large enough.

The findings discussed above provide important guidance for significantly enhancing the caloric effects and reducing the hysteresis loss through multi-field regulation. However, in these studies, the applied stress usually kept constant and the coupling term driven by the combined application of magnetic field and pressure was not taken into account. The main obstacle lies in the fact that it is difficult to realize a continuously changing stress field in reality. So far, only two experimental studies of multicaloric effect have considered the coupling terms, where the function of magnetization as pressure was obtained by a nonlinear numerical simulation based on the magnetization data collected under different pressures. One is the Fe49Rh51[17] and the other is the Ni50Mn35In15 alloys.[15] However, it is worth noting that the pressure and magnetic fields have opposite effects on the magnetostructural transition for these two alloys. Currently, almost no study has been conducted on systems in which the magnetic field and hydrostatic pressure drive the phase transition in the same direction.

4.1. FeRh alloys

FeRh alloys have attracted considerable attention in recent years due to their large magnetocaloric,[70] elastocaloric,[71] and barocaloric[72] effects. FeRh is an ideal material for studying the fundamentals of multicaloric effect, which undergoes a magnetoelastic transition from a low temperature AFM to a high temperature FM phase. The crystal structure remains the CsCl-type cubic (Pm3m) but the lattice expands isotropically by ΔV/V ∼ 1% on heating during the transition for Fe49Rh51 alloys.[17,72] Therefore, the application of magnetic field and hydrostatic pressure has opposite effect on the magnetoelastic transition. The former drives the transition to low temperature while the latter drives the transition to high temperature (Fig. 1(a)). In other words, Fe49Rh51 exhibits inverse magnetocaloric effect and conventional barocaloric effect. A proper combination of pressure and magnetic field can not only achieve a significant broadening of the cooling temperature zone, but also reverse the sign of the entropy change from conventional to inverse. In 2015, Stern-Taulats et al.[17] performed magnetic measurements under different hydrostatic pressures, and then the relationship between the magnetization and the pressure (M–P curve) at a specific temperature was obtained by a nonlinear numerical simulation (Fig. 1(b)).

Fig. 1. (a) Thermomagnetic curves of Fe49Rh51 alloy under different magnetic fields and pressures. (b) Isothermal magnetization as a function of pressure for Fe49Rh51 at 300 K and 320 K. (Reprinted with permission from Ref. [17]. Copyright 2017, APS Publishing Limited).

By using the thermodynamic relationship in Section 2, quantitative data of the entropy changes of the coupled-caloric and multicaloric effects were obtained based on the M–P curves. Figure 2 shows the temperature dependent entropy changes of multicaloric, single magnetocaloric, single barocaloric, and coupled-caloric effects under the combined application of hydrostatic pressure and magnetic field. It can be observed that, for the thermodynamic path where the magnetic field is applied and the pressure is removed, the single magnetocaloric (Fig. 2(a), green line) and the single barocaloric (Fig. 2(a), blue line) effects are both limited to a narrow temperature range. While the multicaloric effect (Fig. 2(a), red line) shows a significantly broadened cooling temperature region, which is contributed by the cross-response, i.e., the so called coupled-caloric effect (Fig. 2(a), orange line). However, for the thermodynamic path where the magnetic field and pressure are both applied at the same direction, the combination of the inverse magnetocaloric effect and the conventional barocaloric effect will produce a special multicaloric response in Fe49Rh51, as shown in Fig. 2(b). At lower magnetic fields, the conventional barocaloric effect plays a dominant role, and the application of pressure reduces the total entropy change. As the magnetic field increases, the effect of the inverse magnetocaloric effect gradually increases. When the magnetic field increases to a certain value, the sign of the multicaloric effect in Fe49Rh51 alloy changes from negative to positive, and the cooling temperature region shifts to lower temperature. It proves that, due to the different performance of the coupled-caloric effect, the sign of the multicaloric response can be finely adjusted by application of magnetic field and hydrostatic pressure. These performances of the thermodynamic path dependence of the multicaloric effect are closely related to the opposite effects of magnetic field and pressure on the phase transition. However, the physical mechanism of the coupled-caloric effect is not involved in this work, which requires further research.

Fig. 2. (a) Temperature dependence of the multicaloric effect (red line), single barocaloric effect under zero magnetic field (blue line), single magnetocaloric effect at 5 kbar (green line), and the coupled-caloric effect (orange line) in Fe49Rh51 corresponding to the application of a 2 T magnetic field and the removal of 5 kbar pressure. (b) Temperature dependence of the multicaloric effect for combined application of magnetic field and hydrostatic pressure. (Reprinted with permission from Ref. [17]. Copyright 2017, APS Publishing Limited).
4.2. Ni–Mn-based Heusler alloys

In order to further study the physical mechanism behind the coupled-caloric effect, Liang et al. investigated the coupled-caloric effect driven by combined hydrostatic pressure and magnetic field in Ni50Mn35In15 alloy by using the measured magnetization data under different pressures.[15] It is worth noting that the driving direction of pressure for the martensitic magnetostructural transition of the off-stoichiometric Heusler alloy Ni2Mn1 + xIn1 − x is also opposite to that of the magnetic field. The off-stoichiometric Heusler alloy Ni2Mn1+x M1 − x (M = Ga, Sn and In, 0 < x < 1) undergoes a martensitic transformation from a high temperature L21 cubic structure to a closely packed martensite phase with low crystal symmetry.[73] Many important functional properties related to the martensitic transition have been reported, such as metamagnetic shape memory effect,[74] magnetic superelasticity,[75] giant magnetocaloric effect, and magnetoresistance.[76] The application of hydrostatic pressure compresses the lattice and shortens the nearest neighboring atomic distance of Mn–Mn. As a response, the AFM exchange between the Mn atoms enhances, resulting in the shift of the martensitic transition temperature (TM) to higher temperature.[77] Meanwhile, the alloys exhibit a big difference of magnetization between the FM austenitic and non-magnetic/PM martensitic phases near the transition temperature. The resultant large difference of Zeeman energy ensures that the martensitic transition can be driven to lower temperature by an external magnetic field.[78] Therefore, the off-stoichiometric Ni2Mn1+xIn1−x is also an ideal platform for investigating the fundamentals of multicaloric effect driven by magnetic field and pressure. Studies indicated that,[15] in the temperature region of phase transition for Ni50Mn35In15 alloy, the effect of pressure on magnetic properties can be expressed by the change of magnetic volume coupling coefficient χ12 caused by pressure. The macroscopic physical meaning of χ12 refers to the change of magnetism driven by the external pressure at a certain temperature in the phase transition region. By measuring the thermomagnetic curves under different magnetic fields and pressures, the relationship between magnetization and pressure at a specific temperature (M–P curve) can be obtained by nonlinear fitting. Then, the magnetic volume coupling coefficient χ12 is derived from the M–P curves by the equation χ12 = (∂ M/∂ P)T,μ0H. Figure 3 shows the colored contour map and two-dimensional (2D) plots of magnetic volume coupling coefficient χ12 as functions of pressure and temperature under 5 T magnetic field. With the increase of pressure, the peak position of χ12 gradually moves to higher temperature, and the peak always appears near TM regardless of the pressure. It is worth noting that, according to Eq. (5), the coupled-caloric effect is the double integral of the magnetic volume coupling coefficient χ12 (), so the evolution of χ12 with pressure and temperature directly reflects the characteristic behavior of the coupling caloric effect.

Fig. 3. (a) Colored contour map and (b) two-dimensional plots of magnetic volume coupling coefficient χ12 as functions of pressure and temperature. (Reprinted with permission from Ref. [15]; licensed under a Creative Commons Attribution (CC BY) license).

The coupled-caloric effects and magnetocaloric effects under certain pressure have been calculated based on the M–P and M–H curves using thermodynamic formulas in Section 2. The application of different pressures and the removal of magnetic field from 5 T to 0 were chosen as the thermodynamic path. For the entropy change of the coupled-caloric effect (Figs. 4(a) and 4(b)), a negative peak gradually increases in width and depth with increasing pressure near a low temperature of 264 K, while a positive peak forms in the high temperature region (Figs. 4(a) and 4(b)). In other words, the entropy change of the coupled-caloric effect shows a separation of positive and negative peaks. Comparison of the entropy change of the calculated and experimentally measured magnetocaloric effects indicates the caloric effect driven by magnetic field under a certain pressure is the magnetocaloric effect at ambient pressure adjusted by the coupled-caloric effect (Fig. 4(c)). The negative peak of the coupled-caloric effect in the low temperature range compensates the entropy change at ambient pressure. While the positive peak of the coupled-caloric effect, which reflects the evolution of magnetic-structural coupling with pressure, contributes to the entropy change at high pressure. Although the pressure of 9.95 kbar reduces the change in magnetization (ΔM) across the TM by 20%, the contribution of the coupled-caloric effect makes the magnetic entropy change enhanced by 8%. Via quantitatively analyzing the coupled-caloric effect, the essence of the regulated magnetocaloric effect by pressure is revealed in this work, which is of significance for designing new materials based on the magnetostructural coupling strength and its sensitivity to pressure.

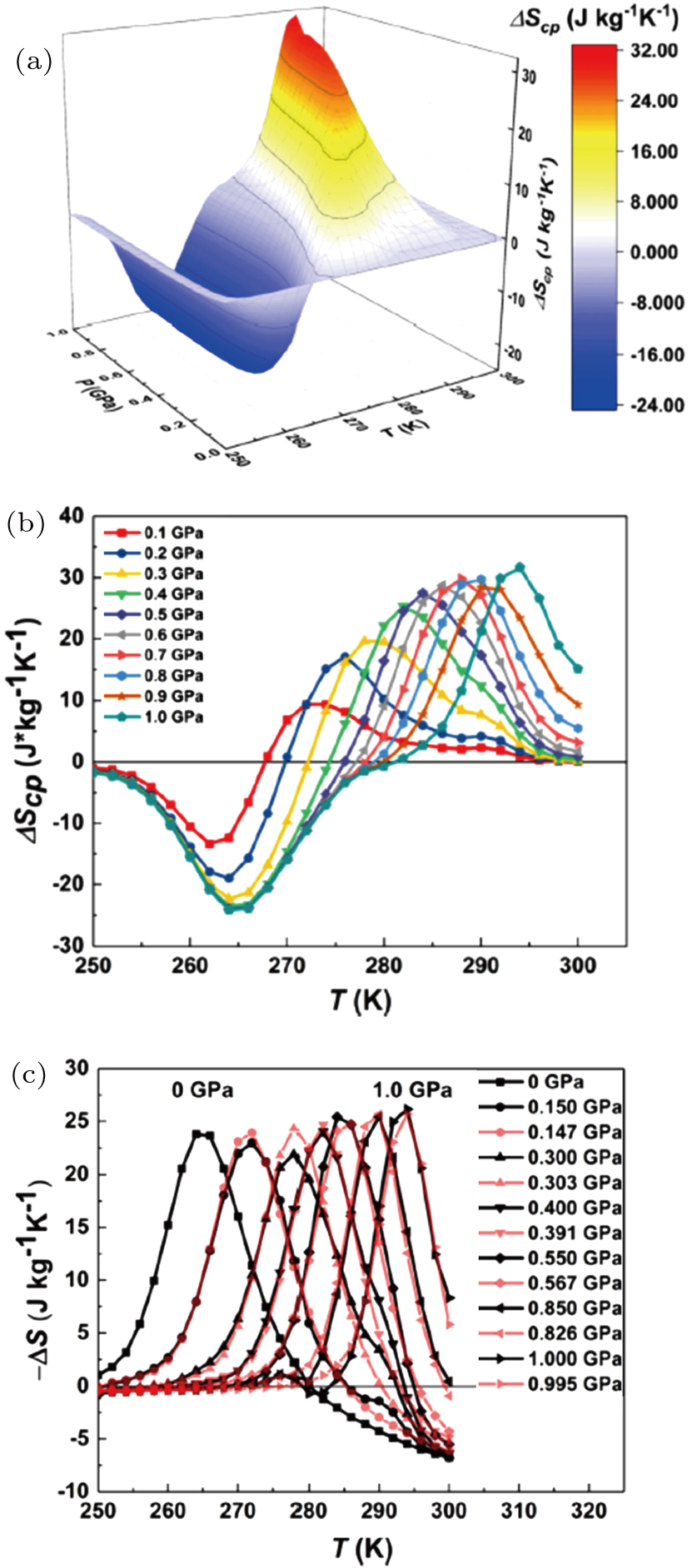Fig. 4. (a) The 3D and (b) 2D plots of the coupled-caloric effect as a function of pressure and temperature for a magnetic field change of 5–0 T. (c) Comparison of the entropy change at ambient pressure adjusted by the coupled-caloric effect and the magnetocaloric results at a specific pressure calculated using Maxwell relation. (Reprinted with permission from Ref. [15]; licensed under a Creative Commons Attribution (CC BY) license).
5. Outlook

For the material with first-order transition, the multicaloric effect driven by multiple fields can overcome some inherent limitations of single caloric effect by improving its thermal response and reversibility. Quantitative analysis about the coupling term contributed to the multicaloric effect can promote the understanding of the refrigeration process controlled by multiple fields. Through pioneer efforts, the multicaloric effect can be understood theoretically in enough detail. However, due to the limitations of experimental technology, few experimental studies have focused on the coupled-caloric and multicaloric effects. The main obstacle lies in the fact that it is difficult to realize a continuously changing stress field in reality. So far, only two experimental studies of multicaloric effect have considered the coupling terms, where the function of magnetization as pressure was obtained by a nonlinear numerical simulation based on the magnetization data collected under different pressures. One is the Fe49Rh51 and the other is the Ni50Mn35In15 alloys. Although the driving directions of magnetostructural/magnetoelastic transition by magnetic field and hydrostatic pressure are opposite for both alloys, a proper choice of the thermodynamic path can lead to an enhanced and broadened caloric response.

The entropy change of the coupled-caloric effect shows separated positive and negative peaks, and the sign of these two peaks depends on the thermodynamic path of the applied pressure and magnetic field. For the materials with opposite driving directions by magnetic field and hydrostatic pressure, the temperature span of the multicaloric effect can be significantly widened in a thermodynamic path where the magnetic field is applied and the pressure is removed; while, the sign of the multicaloric effect is turned over from negative to positive in the thermodynamic path where the magnetic field and pressure are both applied at the same time. In addition, the expression of the coupled-caloric effect is also critically dependent on the strengthening of the first-order transition nature impacted by pressure. Since the materials with the same driving directions by dual fields are very few, there is no experimental report on the coupled-caloric and multicaloric effects for such systems up to now. However, based on the obtained insights, it can be predicted that the multi-field driving cooling temperature zone will broaden in the same direction if the driving directions of the dual fields are the same. At the same time, the enhancement of the coupled-caloric effect will also innovatively contribute to the multicaloric effect. A combination of the experimental and theoretical methods mentioned above is suggested to be used to systematically study different materials. Such research not only helps to make breakthrough progress in multicaloric cycle refrigeration, but also provides valuable feedback for material developments.

Reference
[1] Gschneidner K A Jr Pecharsky V K Tsokol A O 2005 Rep. Prog. Phys. 68 1479
[2] Franco V Blázquez J S Ipus J J Law J Y Moreno-Ramírez L M Conde A 2018 Prog. Mater Sci. 93 112
[3] Shen B G Sun J R Hu F X Zhang H W Cheng Z H 2009 Adv. Mater. 21 4545
[4] Li L W Yan M 2020 J. Alloys Compd. 823 153810
[5] Zheng X Q Shen B G 2017 Chin. Phys. 26 027501
[6] Li Z X Li K Shen J Dai W Gao X Q Guo X H Gong M Q 2017 Acta Phys. Sin. 66 110701 in Chinese
[7] Neese B Chu B Lu S G Wang Y Furman E Zhang Q M 2008 Science 321 821
[8] Manosa L Planes A 2017 Adv. Mater. 29 1603607
[9] Tušek J Engelbrecht K Eriksen D Dall’Olio S Tušek J Pryds N 2016 Nat. Ener. 1 16134
[10] Moya X Kar-Narayan S Mathur N D 2014 Nat. Mater. 13 439
[11] Morellon L Arnold Z Magen C Ritter C Prokhnenko O Skorokhod Y Algarabel P A Ibarra M R Kamarad J 2004 Phys. Rev. Lett. 93 137201
[12] Hao J Z Hu F X Wang J T Shen F R Yu Z B Zhou H B Wu H Huang Q Z Qiao K M Wang J He J He L H Sun J R Shen B G 2020 Chem. Mater. 10.1021/acschemmater9b03915
[13] Samanta T Lepkowski D L Saleheen A U Shankar A Prestigiacomo J Dubenko I Quetz A Oswald I W H McCandless G T Chan J Y Adams P W Young D P Ali N Stadler S 2015 Phys. Rev. 91 020401
[14] Chauhan A Patel S Vaish R 2015 Acta Mater. 97 17
[15] Liang F X Hao J Z Shen F R Zhou H B Wang J Hu F X He J Sun J R Shen B G 2019 APL Mater. 7 051102
[16] Lisenkov S Mani B K Chang C M Almand J Ponomareva I 2013 Phys. Rev. 87 224101
[17] Stern-Taulats E Castán T Planes A Lewis L H Barua R Pramanick S Majumdar S Mañosa L 2017 Phys. Rev. 95 104424
[18] Pecharsky V K Gschneidner K A Jr. 1997 Phys. Rev. Lett. 78 4494
[19] Hu F X Shen B G Sun J R Zhang X X 2000 Chin. Phys. 9 550
[20] Fujita A Fujieda S Hasegawa Y Fukamichi K 2003 Phys. Rev. 67 104416
[21] Castillo-Villa P O Soto-Parra D E Matutes-Aquino J A Ochoa-Gamboa R A Planes A Mañosa L González-Alonso D Stipcich M Romero R Ríos-Jara D Flores-Zúñiga H 2011 Phys. Rev. 83 174109
[22] Wada H Tanabe Y 2001 Appl. Phys. Lett. 79 3302
[23] ul Hassan N Shah I A Khan T Liu J Gong Y Miao X Xu F 2018 Chin. Phys. 27 037504
[24] Yang H Liu J Li C Wang G L Gong Y Y Xu F 2018 Chin. Phys. 27 107502
[25] Bao L F Huang W D Ren Y J 2016 Chin. Phys. Lett. 33 077502
[26] Zhang H Xing C F Long K W Xiao Y N Tao K Wang L C Long Y 2018 Acta Phys. Sin. 67 207501 in Chinese
[27] Zhang B Zheng X Q Zhao T Y Hu F X Sun J R Shen B G 2018 Chin. Phys. 27 067503
[28] Trung N T Ou Z Q Gortenmulder T J Tegus O Buschow K H J Brück E 2009 Appl. Phys. Lett. 94 102513
[29] Liu J Gottschall T Skokov K P Moore J D Gutfleisch O 2012 Nat. Mater 11 620
[30] Liu Y Phillips L C Mattana R Bibes M Barthelemy A Dkhil B 2016 Nat. Commun. 7 11614
[31] Liu J Gong Y You Y You X Huang B Miao X Xu G Xu F Brück E 2019 Acta Mater. 174 450
[32] Qiao K Hu F Liu Y Li J Kuang H Zhang H Liang W Wang J Sun J Shen B 2019 Nan. Ener 59 285
[33] Guillou F Pathak A K Paudyal D Mudryk Y Wilhelm F Rogalev A Pecharsky V K 2018 Nat. Commun. 9 2925
[34] Scheibel F Gottschall T Taubel A Fries M Skokov K P Terwey A Keune W Ollefs K Wende H Farle M Acet M Gutfleisch O Gruner M E 2018 Ener. Techno 6 1397
[35] Liu Y Zhang G Li Q Bellaiche L Scott J F Dkhil B Wang Q 2016 Phys. Rev. 94 214113
[36] Planes A Castán T Saxena A 2014 Philos. Mag. 94 1893
[37] Planes A Castán T Saxena A 2016 Philos. Trans. R. Soc. 374 20150304
[38] Chauhan A Patel S Vaish R 2015 Acta Mater. 89 384
[39] Li L W 2016 Chin. Phys. 25 037502
[40] Zheng X Q Shen J Hu F X Sun J R Shen B G 2016 Acta Phys. Sin. 65 217502 in Chinese
[41] Zhang Y 2019 J. Alloys Compd. 787 1173e
[42] Hao Z H Wang H Y Zhang Q Mo Z J 2018 Acta Phys. Sin. 67 247502 in Chinese
[43] Wu X F Guo C P Cheng G Li C R Wang J Du Y S Rao G H Du Z M 2019 Chin. Phys. 28 057502
[44] Mo Z J Sun Q L Shen J Yang M Li Y J Li L Liu G D Tang C C Meng F B 2018 Chin. Phys. 27 017501
[45] De Sousa V Von Ranke P Gandra F 2011 J. Appl. Phys. 109 063904
[46] Li L W Yuan Y Xu C Qi Y Zhou S Q 2017 AIP Adv. 7 056401
[47] Wang X Wang L Ma Q Sun G Zhang Y Cui J 2017 J. Alloys Compd. 694 613
[48] Chen J Zheng X Q Dong Q Y Sun J R Shen B G 2011 Appl. Phys. Lett. 99
[49] Delyagin N N Krylov V I Rozantsev I N 2007 J. Magn. Magn. Mater. 308 74
[50] Chen J Zheng X Q Dong Q Y Sun J R Shen B G 2011 Appl. Phys. Lett. 99 122503
[51] Zheng X Q Chen J Xu Z Y Mo Z J Hu F X Sun J R Shen B G 2014 J. Appl. Phys. 115 17A938
[52] Ma Y F Tang B Z Xia L Ding D 2016 Chin. Phys. Lett. 33 126101
[53] Wu C Ding D Xia L 2016 Chin. Phys. Lett. 33 016102
[54] Chen X Zhao M H 2018 Acta Phys. Sin. 67 197501 in Chinese
[55] Zhang H Shen B G 2015 Chin. Phys. 24 127504
[56] Dong Q Shen B Chen J Shen J Zhang H Sun J 2009 J. Appl. Phys. 105 07A305
[57] Klimczak M Talik E 2010 J. Phys.: Conf. Ser. 200 092009
[58] Kaštil J Javorský P Kamarad J Diop L Isnard O Arnold Z 2014 Intermetallics 54 15
[59] Fickenscher T Rodewald U C Niepmann D Mishra R Eschen M Pöttgen R 2005 Z. Naturforsch. 60 271
[60] Ding D Zhang Y Q Xia L 2015 Chin. Phys. Lett. 32 106101
[61] Dong X Feng J Yi Y Li L 2018 J. Appl. Phys. 124 093901
[62] Fisher I Islam Z Canfield P 1999 J. Magn. Magn. Mater. 202 1
[63] Hermes W Rodewald U C Pöttgen R 2010 J. Appl. Phys. 108 113919
[64] Li L Niehaus O Kersting M Pöttgen R 2015 Intermetallics 62 17
[65] Li L Nishimura K Kadonaga M Qian Z Huo D 2011 J. Appl. Phys. 110 043912
[66] Lisenkov S Ponomareva I 2012 Phys. Rev. 86 104103
[67] Ponomareva I Lisenkov S 2012 Phys. Rev. Lett. 108 167604
[68] Planes A Stern-Taulats E Castán T Vives E Mañosa L Saxena A 2015 Mater. Toda.: Procee 2 S477
[69] Meng H Li B Ren W Zhang Z 2013 Phys. Lett. 377 567
[70] Nikitin S A Myalikgulyev G Tishin A M Annaorazov M P Asatryan K A Tyurin A L 1990 Phys. Lett. 148 363
[71] Nikitin S A Myalikgulyev G Annaorazov M P Tyurin A L Myndyev R W Akopyan S A 1992 Phys. Lett. 171 234
[72] Stern-Taulats E Planes A Lloveras P Barrio M Tamarit J L Pramanick S Majumdar S Frontera C Mañosa L 2014 Phys. Rev. 89 214105
[73] Kübler J William A R Sommers C B 1983 Phys. Rev. 28 1745
[74] Kainuma R Imano Y Ito W Sutou Y Morito H Okamoto S Kitakami O Oikawa K Fujita A Kanomata T Ishida K 2006 Nature 439 957
[75] Krenke T Duman E Acet M Wassermann E F Moya X Manosa L Planes A 2005 Nat. Mater. 4 450
[76] Yu S Y Liu Z H Liu G D Chen J L Cao Z X Wu G H Zhang B Zhang X X 2006 Appl. Phys. Lett. 89 162503
[77] Sharma V K Chattopadhyay M K Roy S B 2011 J. Phys.: Condens Matter 23 366001
[78] Quetz A Koshkid’ko Y S Titov I Rodionov I Pandey S Aryal A Ibarra-Gaytan P J Prudnikov V Granovsky A Dubenko I Samanta T Cwik J Sánchez Llamazares J L Stadler S Lähderanta E Ali N 2016 J. Alloys Compd. 683 139