† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2018YFA0305700), the National Natural Science Foundation of China (Grant Nos. 11834016, 11874400, and 11921004), the Beijing Natural Science Foundation, China (Grant No. Z190008), the Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (Grant No. QYZDB-SSW-SLH013), and the CAS Interdisciplinary Innovation Team. ZLD and HDZ acknowledge the support of Grant No. NSF-DMR-1350002. JSZ acknowledges the support of NSF DMR Grant No. 1729588.
The cubic pyrochlore Dy2Pt2O7 was synthesized under 4 GPa and 1000 °C and its magnetic and thermodynamic properties were characterized by DC and AC magnetic susceptibility and specific heat down to 0.1 K. We found that Dy2Pt2O7 does not form long-range magnetic order, but displays characteristics of canonical spin ice such as Dy2Ti2O7, including (1) a large effective moment 9.64 μB close to the theoretical value and a small positive Curie–Weiss temperature θCW = +0.77 K signaling a dominant ferromagnetic interaction among the Ising spins; (2) a saturation moment ∼4.5 μB being half of the total moment due to the local 〈111〉 Ising anisotropy; (3) thermally activated spin relaxation behaviors in the low (∼1 K) and high (∼20 K) temperature regions with different energy barriers and characteristic relaxation time; and most importantly, (4) the presence of a residual entropy close to Pauling’ estimation for water ice.
Geometrically frustrated magnets can display rich and diverse phenomena, providing an excellent platform for experimental realizations of collective magnetism that was predicated theoretically.[1,2] The recognition of a spin ice state in the cubic pyrochlore compounds Ho2Ti2O7 and Dy2Ti2O7 represents such an example that successfully maps to the well-known water–ice problem.[3–6] In these pyrochlores, the magnetic rare-earth ions, Ho3+ or Dy3+, with a large magnetic moment of ∼ 10 μB reside on the vertices of the corner-sharing tetrahedra, forming a geometrically frustrated lattice. A uniaxial local crystalline electric field (CEF) around Ho3+ or Dy3+ results in a nearly perfect easy-axis anisotropy, forcing the rare-earth’ spin to point along the local 〈111〉 axis that joins the centers of two neighboring tetrahedra.[7,8] The combination of dipolar and magnetic exchange interactions favors ‘two-in, two-out’ spin configurations on each tetrahedron, which has been termed ‘spin ice’ in direct analogy to the ‘two-short, two-long’ proton bond disorder in water ice. The Pauling’ zero-point entropy SP = (R/2)ln(3/2), where R is the ideal gas constant, for water ice has also been confirmed in the spin ices having a macroscopically degenerate ground state.[5]
The low-temperature magnetic properties of a pyrochlore spin ice are mainly controlled by the magnetic exchange (Jnn) and the dipole–dipole interaction (Dnn) of the nearest-neighbor spins. For these pyrochlore spin ice materials, Jnn is usually antiferromagnetic, while Dnn is ferromagnetic and can be calculated as 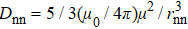
Besides the chemical pressure effects caused by the size of B-cation in Ln2B2O7 (Ln = rare earth), our recent studies on the platinum-based pyrochlores Ln2Pt2O7 have revealed an additional effect of the nonmagnetic Pt4+ ions,[12,13] i.e., the spatially more extended Pt-5d orbitals and thus the enhanced Pt 5d–O 2p hybridizations can modify the CEF and influence the exchange interactions. In comparison with Gd2B2O7 (B = Ge, Ti, Sn), the antiferromagnetic transition temperature of Gd2Pt2O7 is substantially enhanced because the empty Pt-eg orbitals provide extra superexchange pathways.[13] Thus, we expect an alternative routine to modify Jnn/Dnn in the Pt-based Ising pyrochlores.
In this work, we have prepared the pyrochlore compound Dy2Pt2O7 under high pressure, and characterized its magnetic and thermodynamic properties via magnetic susceptibility and specific heat measurements down to 0.1 K. We find that Dy2Pt2O7 does not exhibit any long-rang magnetic order at low temperature, but displays canonical spin ice characteristics, including the thermally activated spin dynamics and the presence of Pauling’ zero-point entropy. By comparing the low-temperature magnetic specific heat to DSIM, we obtain a ratio of Jnn/Dnn = −0.56 for Dy2Pt2O7. Our results demonstrate that Dy2Pt2O7 is a new spin ice compound with enhanced superexchange interaction Jnn.
The sample preparations and characterizations in the present study are similar to those performed in our previous work.[12] The cubic pyrochlore Dy2Pt2O7 sample was prepared under 4 GPa and 1000 °C by using a Kawai-type multianvil module (Max Voggenreiter GmbH). The resultant high-pressure products were first washed with warm aqua regia to remove a small amount of platinum metal and unreacted Dy2O3; the obtained powders were then pressed into pellets and subjected to heat treatment at 900 °C for 10 h to facilitate the measurements of the bulk physical properties.
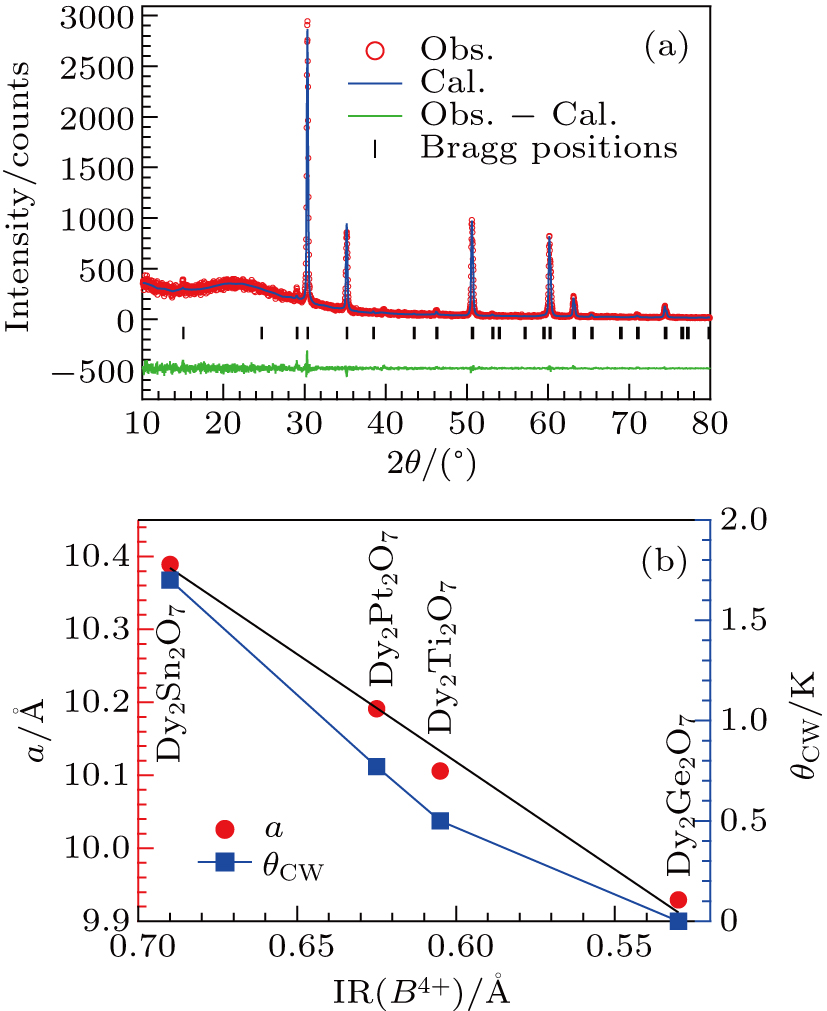
Phase purity of the obtained powder and pellet samples was examined by powder x-ray diffraction (XRD) at room temperature. Structural parameters were extracted from the XRD patterns via Rietveld refinement with the FullProf program. DC magnetic susceptibility was measured with a commercial magnetic property measurements system (MPMS-III, Quantum Design) in the temperature range from 1.8 K to 300 K under an external magnetic field of μ0H = 0.1 T. AC magnetic susceptibility measurements in the temperature range 2 K < T < 50 K were performed in a physical property measurement system (PPMS, Quantum Design). AC susceptibility measurements from 70 mK to 2 K were carried out in an Oxford dilution refrigerator with the mutual induction method; an excitation current of ∼ 1 mA with frequencies ranging from 117 Hz to 1517 Hz was applied to the primary coil during the measurements. Specific-heat data down to 0.1 K were collected by the PPMS with a dilution refrigerator insert.
Figure
The magnetic properties of Dy2Pt2O7 were first characterized by DC magnetization measurements in the temperature range from 1.8 K to 300 K. Figure
The isothermal magnetization M(H) curves measured in fields up to 5 T at 2 K and 5 K are shown in Fig.
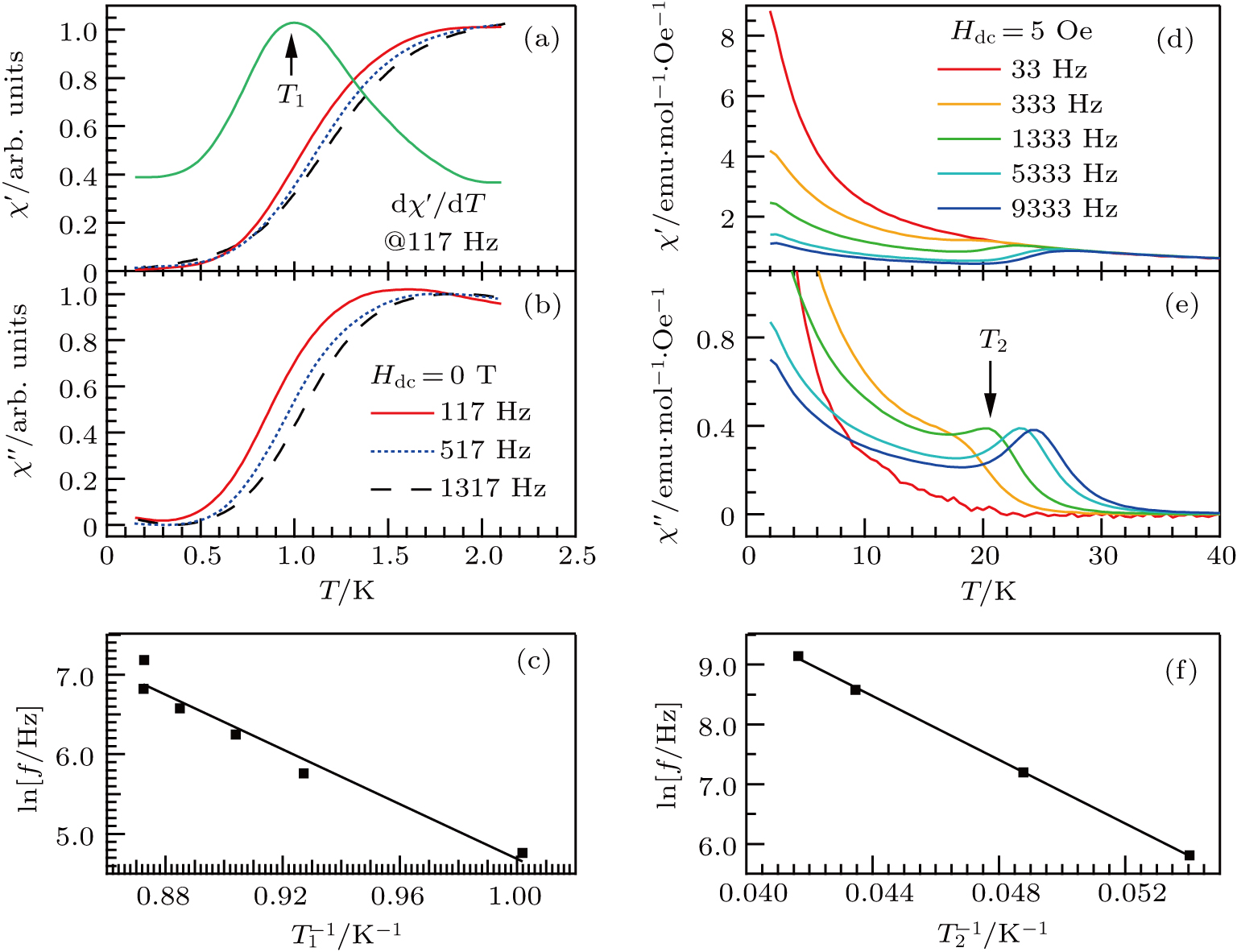
Figure 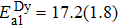

Another distinct feature in the AC susceptibility of Dy-pyrochlore spin ices is the presence of a high-temperature peak around 15 K.[17–20] Similar behaviors are also observed in Dy2Pt2O7, Figs. 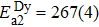

Figure
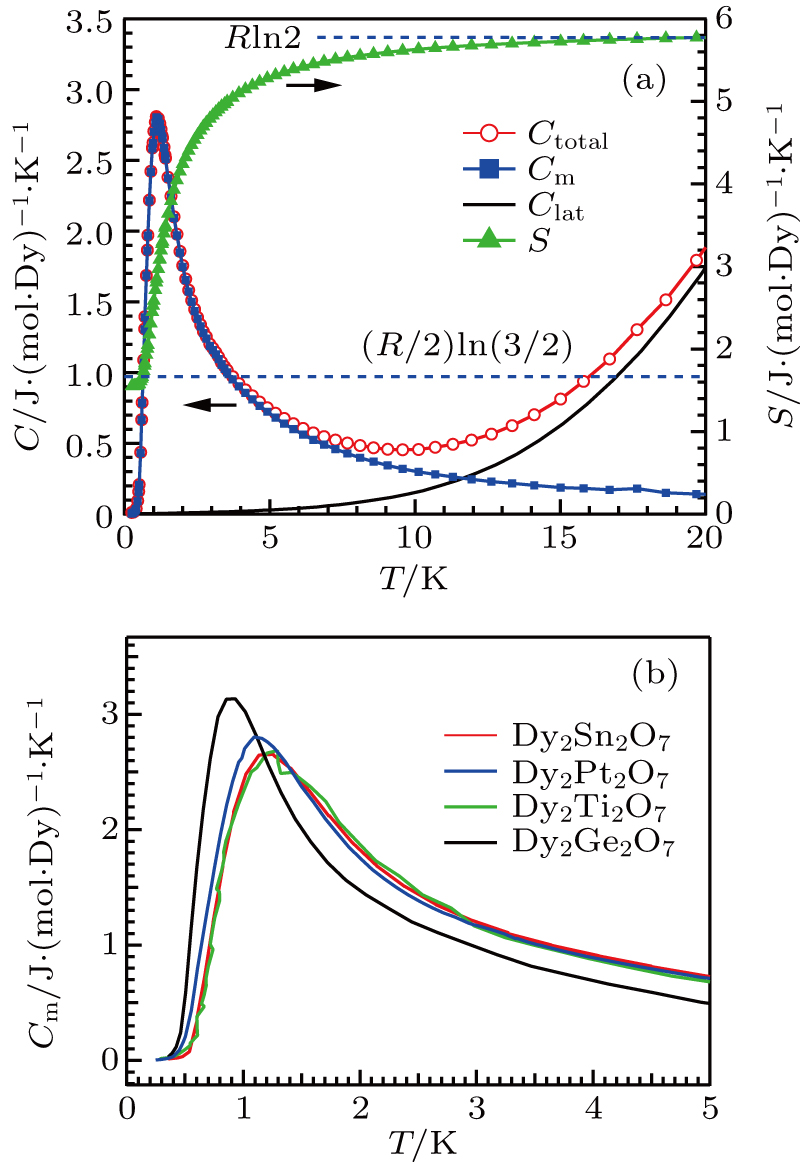
Based on these above characterizations, we can conclude that Dy2Pt2O7 is a new spin ice characterized by: (i) a large effective moment 9.64 μB close to the theoretical value, and a small positive Curie–Weiss temperature θCW = +0.77 K signaling a dominant ferromagnetic interaction among the Ising spins; (ii) a saturation moment ∼ 4.5 μB being half of the total moment due to the local 〈111〉 Ising anisotropy; (iii) thermally activated spin relaxation behaviors in the low (∼ 1 K) and high (∼ 20 K) temperature regions with different energy barriers and characteristic relaxation time; and most importantly, (iv) the presence of a residual entropy close to Pauling’ estimation for water ice.
Although it is not unexpected that Dy2Pt2O7 displays typical behaviors of canonical spin ice, the effects of non-magnetic Pt4+ are noteworthy. For this purpose, we have compared the Cm of Dy2Pt2O7 with those of Dy2B2O7 (B = Sn, Ti, Ge) in Fig.
| Table 1. Lattice parameter and selected magnetic parameters for the Dy-pyrochlore spin ices Dy2B2O7 (B = Ge, Ti, Pt, Sn). . |
In summary, we have synthesized the cubic pyrochlore Dy2Pt2O7 under 4 GPa and 1000 °C, and confirmed it to be a new classical spin ice as Dy2Ti2O7. The magnetic specific heat of Dy2Pt2O7 signals a moderate enhancement of |Jnn|, but the ratio Jnn/Dnn = −0.56 remains located in the spin ice regime as predicted by DSIM. Our work demonstrates that the Jnn/Dnn can be effectively tuned by replacing the B-site cation of Ising pyrochlores. But further explorations are needed to realize a transition from spin ice to an antiferromagnetically ordered state by varying Jnn/Dnn in a larger range as predicated by the DSIM.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] |