† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0204600) and the Fundamental Research Funds for the Central Universities of Central South University, China (Grant No. 2019zzts424).
An analytical drain current model on the basis of the surface potential is proposed for indium–gallium zinc oxide (InGaZnO) thin-film transistors (TFTs) with an independent dual-gate (IDG) structure. For a unified expression of carriers’ distribution for the sub-threshold region and the conduction region, the concept of equivalent flat-band voltage and the Lambert W function are introduced to solve the Poisson equation, and to derive the potential distribution of the active layer. In addition, the regional integration approach is used to develop a compact analytical current–voltage model. Although only two fitting parameters are required, a good agreement is obtained between the calculated results by the proposed model and the simulation results by TCAD. The proposed current–voltage model is then implemented by using Verilog-A for SPICE simulations of a dual-gate InGaZnO TFT integrated inverter circuit.
Amorphous indium–gallium zinc oxide thin film transistors (a-InGaZnO TFTs) are advantageous for the next-generation display, due to the merits of high driving ability, good reliability, and mature process over large fabrication areas.[1–5] To further extend the applications of InGaZnO TFTs, the independent dual-gate structure is preferably adopted to adjust the threshold voltage in a wider range. Dual-gate InGaZnO TFTs render circuit response fast and power consumption low.[6–8] Previous researches show that the threshold voltage of the driving transistor can be adjusted dynamically by discharging the auxiliary gate, which benefits good compensation effect for active matrix organic light emitting diode (AMOLED) displays.[9] In the case of system-on-panel circuit integrations, it was proposed that high voltage–gain amplifiers be replaced by the dual-gate InGaZnO TFTs with differential inputs.[10] Although some dual-gate InGaZnO TFT circuits were implemented and measured, there have been no mature analytical current–voltage models for dual-gate InGaZnO TFTs up to date, which brings the difficulties in designing TFTs circuit by using SPICE tools.
SPICE simulations require an analytical TFT model, which is efficient and timing saving, compared with numerical calculations.[11,12] In recent years, the lack of appropriate analytical current–voltage model for InGaZnO TFTs attracts widespread attention from academic and industry. Perumal et al.[13] presented a compact model of InGaZnO TFTs on the basis of metal–oxide–semiconductor field-effect transistor (MOSFET) SPICE model. But the model is not accurate enough. Tsuji et al.[14] developed an efficient model for numerical simulations of single-gate InGaZnO TFTs. Cai et al.[15] successfully developed a drain current–voltage model for dual-gate InGaZnO TFTs, which is suitable for sub-threshold and above-threshold operating regions. However, the presented model is strongly dependent on the pre-determined threshold voltage, which is also difficult to calculate from physical parameters.
In this paper, an analytical current model is developed for independent dual-gate (IDG) InGaZnO TFTs on the basis of the surface potential. The effective carrier density is introduced and the Lambert function is used to solve the Poisson equation. It was proposed that the equivalent flat band voltage, i.e., VFB, can be used to characterize the phenomenon that the sub-threshold potential of the device is linearly modulated by the top gate voltage, i.e., VGT. In addition, the Lambert function is simplified by solving the potential of the sub-threshold region and the conduction region, separately. On the basis of the derived surface potential, the current–voltage expression can be derived by solving the dual integration of Pao–Sah’s law. The proposed current–voltage model is applied to the SPICE simulation and validated effectively.
Figure
As an amorphous N-type semiconductor material, intrinsically, InGaZnO has a surface potential dependent on free electrons and localized electrons. Hence the potential of InGaZnO film follows the Poisson’s equation

Using the Boltzmann distribution function, the effective carrier density can be expressed as[16]

Due to the fact that

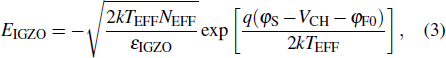
For the interface between the gate-insulator and the InGaZnO layer, the Gaussian law can be used to relate the top and bottom gate voltage and the boundary electrical field together. Consequently, it can be derived that
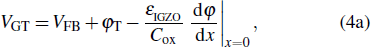
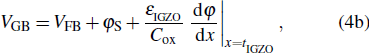






On the basis of the obtained analytical surface potential, the current–voltage model for IDG InGaZnO TFT is developed as follows. According to the Pao–Sah formula, the drain–source current of the IDG InGaZnO TFT is


Then the partial derivative of E (Eq. (
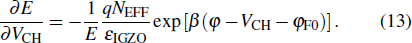

Figure
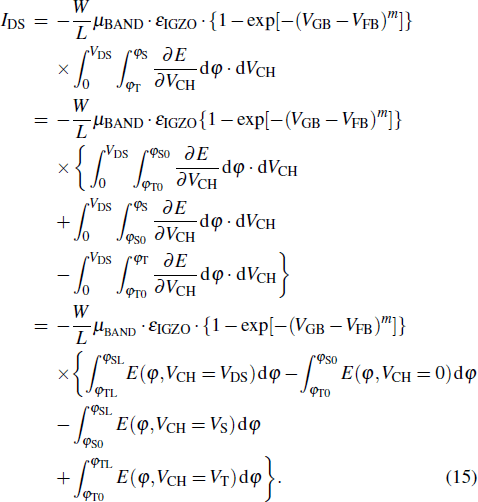
 | Fig. 2. Plots of surface potential φS and top potential φT versus channel voltage for IDG InGaZnO TFT, with colored area referring to integration region. |
By directly integrating Eq. (


By combining Eq. (
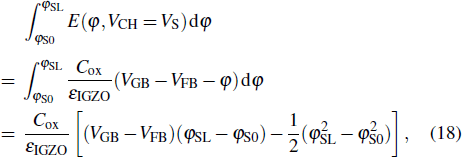
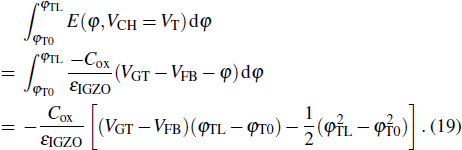
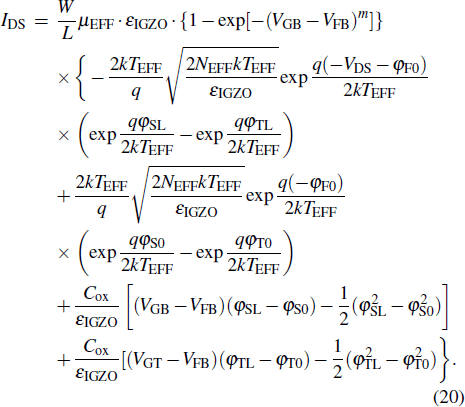
To verify the developed model, comparisons are carried out between the calculated and TCAD simulated results. The investigated TFT structure is shown in Fig.
| Table 1. InGaZnO TFT parameters for TCAD simulation and model calculation. . |
Figure
 | Fig. 3. Simulated and calculated plots of surface potential φS versus bottom gate voltage VGB for three different values of VGT. |
Figure
 | Fig. 4. Comparison between simulated and calculated transfer characteristics of IDG a-InGaZnO TFT for three different values of VGT. |
 | Fig. 5. Comparison between calculated and simulated output characteristics of IDG a-InGaZnO TFT with VGT = −5 V for various values of VGS. |
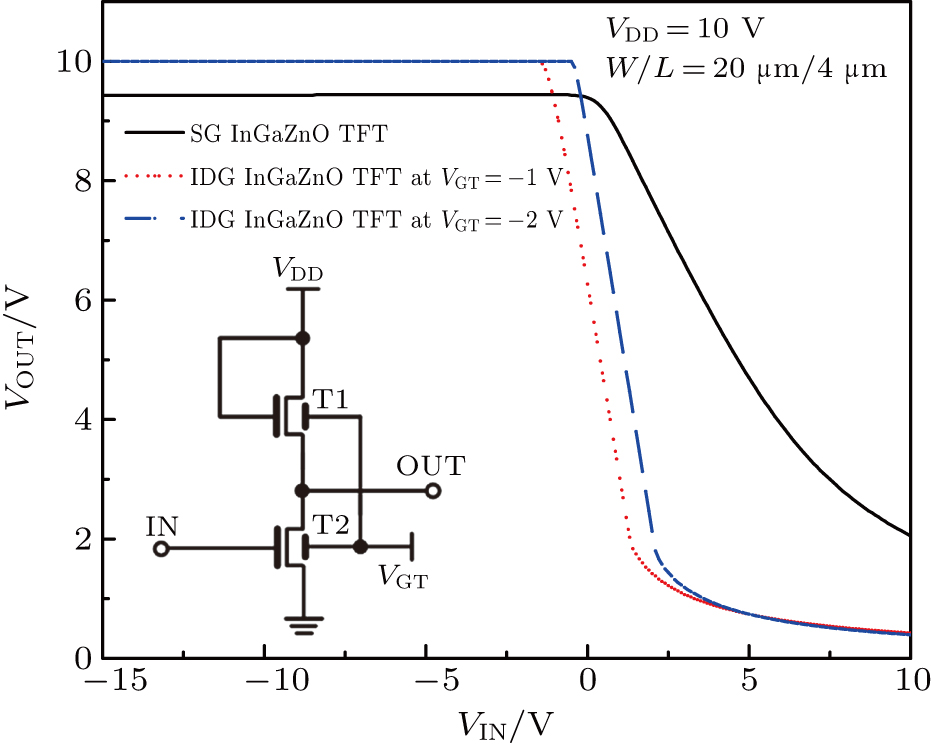
The proposed model is integrated into circuit simulations with Verilog-A. Figure
In this work, an analytical drain current model for independent dual-gate InGaZnO TFT is established based on the surface potential. Equivalent flat band voltage VFB is introduced to represent the linear surface potential modulation effect of the top gate voltage VGT. Following the Pao–Sah’s law, regional integration is carried out in detail to obtain a continuous current–voltage model for the independent dual-gate InGaZnO TFTs. Comparisons between the model calculations and the TCAD simulations are carried out, and the results show that both the transfer and output characteristics are in good agreement for different operation regions. Furthermore, in order to verify the effectiveness of IDG InGaZnO TFTs for high-performance circuit designs, the model is applied to an SPICE simulator using Verilog-A, which is helpful in designing the high performance InGaZnO TFT circuit for system on panel circuit integrations.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] |