† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51605418) and the Natural Science Foundation of Hebei Province, China (Grant Nos. E2016203206 and E2019203033).
A coarse-grained molecular dynamics simulation model was developed in this study to investigate the friction process occurring between Fe and polytetrafluoroethylene (PTFE). We investigated the effect of an external load on the friction coefficient of Fe–PTFE using the molecular dynamics simulations and experimental methods. The simulation results show that the friction coefficient decreases with the external load increasing, which is in a good agreement with the experimental results. The high external load could result in a larger contact area between the Fe and PTFE layers, severer springback as a consequence of the deformed PTFE molecules, and faster motion of the PTFE molecules, thereby affecting the friction force and normal force during friction and consequently varying the friction coefficient.
Friction exists at the interface between two surfaces in contact when they slide against each other, and it resists the relative motion that occurs between them. The frictional performance of materials is usually evaluated via the friction coefficient and wear rate.[1–3] A large friction coefficient indicates that a high driving force is required to overcome the frictional resistance, thereby increasing the friction and decreasing the system efficiency. Solid self-lubricating materials possess lower friction coefficients in the absence of lubricants, and therefore, have been widely applied in situations where liquid lubricants cannot be used.[4,5] polytetrafluoroethylene (PTFE) is a self-lubricating material, which is extensively used in engineering fields due to its low friction coefficient, high temperature stability, and chemical resistance.[6] However, the friction coefficient of PTFE is affected by many factors, such as the external load,[7,8] sliding velocity,[9] and operating temperature.[10,11] Furthermore, the external load plays an essential role, thereby attracting researchers to study its mechanisms of influence on the friction coefficient of PTFE.
Bi et al.[12] studied the effect of the external load on the friction coefficient of PTFE through experiments. The results showed a severe deformation of the PTFE asperities with an increase in the external load, thereby increasing the contact area between PTFE and its counter surface and reducing the friction coefficient of PTFE. Wang et al.[13] concluded that a large external load leads to the formation of a PTFE transfer film on its counter surface. The transferred PTFE converts the friction between PTFE and its counter surface to PTFE–PTFE friction, and consequently decreasing the friction coefficient. Qiu et al.[14] defined the ratio of a larger load to a smaller load of a step load as the load ratio and found that a large load ratio is beneficial for the transfer film formation. Moreover, when PTFE is operated under variable loading, the higher dynamic load may result in heat build-up, thus, affecting the friction coefficient of PTFE.[6]
The above-mentioned experimental studies are beneficial for exploring the mechanisms of influence of an external load on the friction coefficient of PTFE. However, the PTFE friction mechanisms, acquired from friction tests, are usually speculated by comprehensive analysis of the sample in terms of morphological features and composition variation. To completely understand the mechanisms of influence of an external load on the friction coefficient of PTFE, we would need to investigate the frictional changes of the PTFE molecules at an atomic level. PTFE is a semi-crystalline polymer that presents a crystalline and amorphous structure.[15] Barry et al.[16–19] studied the tribological characteristics of PTFE with a crystalline structure by simulating a molecular dynamics (MD) friction model with regular distributed PTFE molecules. Their simulation results showed that both the friction force and normal force increase with an increase in the load applied to the upper PTFE layer.[17,19] Pan et al.[20] built a two-layer PTFE–PTFE friction model to analyze the frictional mechanisms of PTFE with an amorphous structure. They found that the friction coefficient of PTFE decreases along with a rise in the external load. This occurs because the normal force has a higher rate of growth than the friction force whenever there is an increase in the external load. Considering that the coarse-grained method could not only represent the characteristic features of polymer, but also reduce the computational time, it is usually used to describe the properties of polymer materials. Li et al.[21] adopted the coarse-grained method to describe the perfluoropolyether (PFPE) spreading process. He et al. built a coarse-grained model to study the static and dynamic properties of a grafted ring polymer.[22] Pan et al.[23] developed a coarse-grained PTFE–PTFE friction model by mapping several atoms into one bead and explored the frictional mechanism of amorphous PTFE. They concluded that the friction force and normal force increase with a rise in the external load. However, the factors behind the rise of the friction force and normal force are unclear. In addition, the published MD models with regard to PTFE friction are mostly used to investigate the friction between PTFE and PTFE.
Furthermore, PTFE usually slides against the steel surfaces.[24,25] For the friction process to be similar to the actual application of PTFE, a steel–PTFE model needs to be developed. Considering that the basis of steel is Fe, we built a Fe–PTFE friction model to analyze the variations of amorphous PTFE during the friction process on the basis of our previously developed coarse-grained PTFE model. The mechanism of influence of an external load on the friction coefficient of the amorphous PTFE was investigated at an atomic level by analyzing the bond energy, bond angle energy, and kinetic energy of amorphous PTFE, and the interaction energy between Fe and PTFE layers. The results obtained would be beneficial for exploring the PTFE frictional mechanism and providing a basis for designing PTFE composites with low friction coefficients and high wear resistance.
Although researchers have investigated the effect of an external load on the friction coefficient of PTFE, the experimental setup and test conditions used would vary. To compare the experimental results with the MD simulation results, the conditions employed for the MD simulation model should be similar to those of the experiments. Therefore, we first designed an experiment to analyze how an externally applied load affects the friction coefficient of steel–PTFE.
We performed the steel–PTFE friction test using Anton Paar high temperature tribometer, as shown in Fig.
We chose α-Fe with a body-centered cubic (bcc) structure to develop the coarse-grained model of Fe. Figure
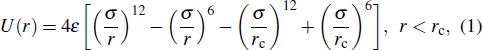
To run the coarse-grained MD simulation, firstly, we initialized ε and σ. Based on the mapping scheme of α-Fe from the all-atom model to bead spring model, the central distance between two neighboring beads (2.8 Å) was set to be the initial value of σ. Considering that the interaction strength between the Fe beads is greater than that between the PTFE beads,[23] the initial value of ε was chosen to be 10 kcal/mol. Then, the size of the coarse-grained model was adjusted using the “fix deform_box” command[26] until it was similar to that of the all-atom model. The simulation was conducted in the Langevin thermostat[28] assuming a microcanonical ensemble (also called NVE ensemble). The size of the system reached 22.93 Å3 after running for 10 ps with a time step of 1 fs, as shown in Fig.
The RDF distribution gi(r) obtained from the coarse-grained Fe model based on the estimated ε and σ might be different from the target RDF distribution gtarget(r). Therefore, we chose to employ iterative Boltzmann inversion (IBI) method[29] to optimize and determine the final values of ε and σ by comparing the difference in RDFs acquired from the all-atom model and coarse-grained model, respectively. This process can be expressed as follows:[29]

The values of ε and σ for the coarse-grained Fe model were determined to be 80 kcal/mol and 2.45 Å, respectively, after a number of iterations. A comparison between the RDF distributions of the coarse-grained model and the all-atom model is shown in Fig.
The interactions between Fe beads and PTFE beads are described while simulating the friction process between Fe and PTFE. In this study, the LJ potential was adopted to describe the interactions between the Fe and PTFE beads, and the combination rule was used to determine the Fe–PTFE interaction parameters as follows:[31]


When simulating the Fe–PTFE friction process, we defined three kinds of non-bonding interactions; the interaction between the Fe beads was called non-bonding_1, the interactions among the PTFE beads were called non-bonding_2, and the interactions between the Fe beads and PTFE beads were called non-bonding_3, as shown in Fig.
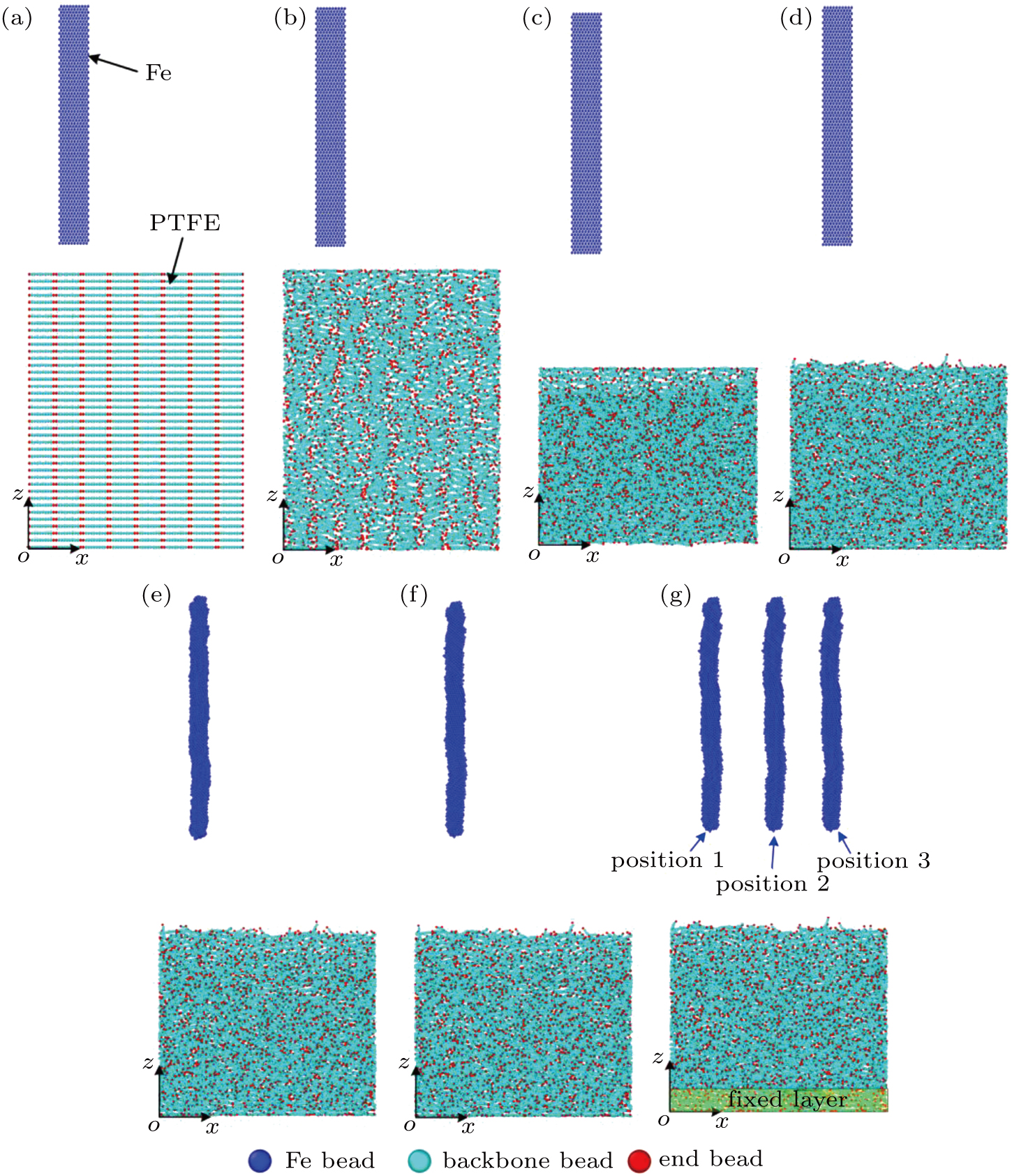
To simulate the friction process between Fe and PTFE, we built a two-layer friction model including Fe and PTFE layers. Figure
In the first step, we ran the PTFE layer until it reached an equilibrium state. To decrease the effect of the regular initial configuration on the simulation results, we adjusted the cutoff distance of the LJ potential (non-bonding_2) until only repulsive forces existed between the PTFE beads. However, the distribution controlled by the repulsive forces cannot be random for a short running time. When run for a long time, spacing between the PTFE molecules is large and they scatter in the simulation box. To randomize the PTFE molecules within a certain space, the “fix wall/reflect” command was used to restrict the motion of the PTFE molecules in the range of 0–280 Å along the z direction. Periodic boundary conditions were applied in x and y directions to remove edge effects. The simulation was performed assuming a canonical ensemble (NVT ensemble) with a time step of 1 fs. The PTFE molecules were randomly distributed after running for 50 ps, as shown in Fig.
In the second step, the relaxation of the Fe layer was conducted. Considering that the simulation would be interrupted if the initial distance between the Fe beads was too short, we assigned a relatively large (∼ 3 Å) initial spacing between the Fe beads, and then slowly compressed the Fe beads along the x direction. The non-bonding interaction (non-bonding_1) would occur in the Fe beads while maintaining a certain distance. Figure
To enable the friction model to reach equilibrium, we continued to run the simulation for 50 ps. The final distributions of the Fe and PTFE beads are shown in Fig.
Figure
 | Fig. 5. Contact and separation processes between Fe and PTFE layers when the external load is 9 MPa and the velocity is 0.05 m/s: (a) T = 0 ps, (b) T = 200 ps. |
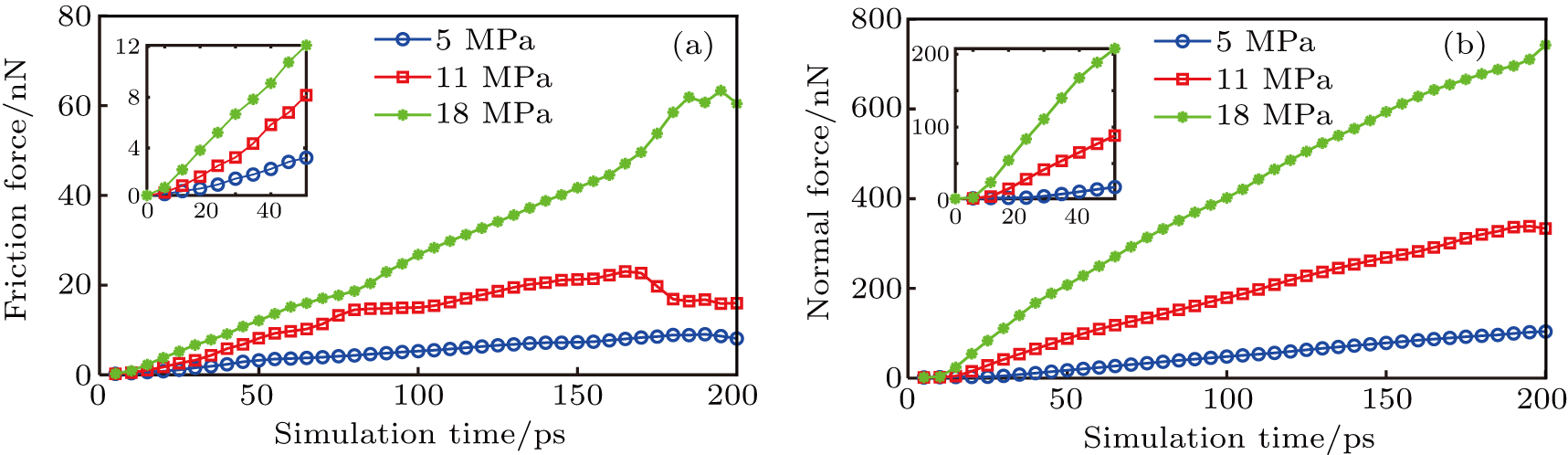
By varying the external load applied on the Fe layer, we can obtain the effect of the external load on the friction coefficient of Fe–PTFE at a fixed velocity of 0.05 m/s. Figure
The deformation of polymers can be described using radius of gyration Rg. A high probability density of Rg indicates that more polymer molecules exist in the corresponding shape. Here, we calculate the x and z components of Rg on the basis of the following equation[32] to elucidate the deformation of PTFE molecules under different external loads:
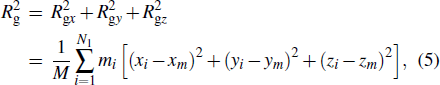
The distributions of the x and z components of Rg are plotted in Fig.
 | Fig. 8. Snapshots of the structural evolution of one PTFE molecular chain under (a) 5 MPa, (b) 11 MPa, and (c) 18 MPa during the friction processes. |
Figure
 | Fig. 9. (a) Bond energy, (b) angle energy, (c) kinetic energy, and (d) Fe–PTFE interaction potential energy as a function of simulation time for different external loads. |
We also analyze the effect of the external load on the friction force and normal force, as shown in Fig.
We developed a coarse-grained molecular dynamics model for α-Fe. Further, a coarse-grained Fe–PTFE friction model was built on the basis of estimated interaction parameters of Fe and PTFE. The influence of the external loads on the friction coefficient of Fe–PTFE was investigated using MD simulation and experiments. It was found that the friction coefficient decreases with the external load increasing. The deformation of the PTFE molecules and the variation of the interaction energies were analyzed to arrive at a reason for this phenomenon. An increase in the external load could increase the depth of the Fe layer immersed into the PTFE layer, thereby enhancing the contact area between the Fe and PTFE layers, eventually leading to an increase in the non-bonding interaction energy. In addition, the springback caused by the deformation of the PTFE molecules may also contribute to the variation of the friction force and normal force. The increase of the PTFE molecular moving velocity under high external load enhances the interaction probability between the Fe beads and PTFE molecules, thereby increasing the Fe and PTFE interaction forces.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |