Highly integrated circuits inevitably lead to high heat flux, which is a bottleneck of Moore’s law. If the heat cannot be released in time, the temperature of the electronic components will rise sharply, leading to short working life, poor performance, as well as unguaranteed stability and reliability. According to statistic data, thermal invalidation is the main failure form of electronic equipments, more than half of electronic equipment failures are caused by poor cooling systems.^[1] The invalidation rate of some electronic components conforms to the 10 °C law, i.e., for every 10 °C rise in temperature, the failure rate doubles.^[2] Electronic components are extremely sensitive to temperature and high temperature is extremely unfavorable to electronic devices, so it is necessary to cool the electronic devices.

A reasonable layout can reduce the temperature of chips under the circumstances of low heat flux. However when the heat flux is high, an effective heat transfer technology needs to be introduced to cool the electronic devices. The heat flow transfers to the package shell first and then is took away by air or other refrigerants.^[3] Materials of the packaging shell selected should be of high thermal conductivity to reduce the internal thermal resistance, such as copper and aluminum. Due to the air gap between heat dissipation devices and packaging shells, thermal interface materials (TIMs) are needed to improve the heat dissipation through the gap. TIMs are usually insulating materials. Polymer materials in shims are most often used as TIMs due to their softness and insulation. Among polymer shim materials, silicone rubber stands out for its relative higher thermal conductivity and good elasticity. Most of conventional TIMs on market are made of silicone oil and silicone rubber.^[4] However, the thermal conductivity of these insulating polymer materials is usually on the order of 10⁻¹ –10⁰ W/(m⋅K).^[4] Therefore, it is necessary to further improve the thermal conductivity of silicone rubber to improve the heat dissipation and meet the increasing requirements of electronic devices. Un-doped silicone rubber has low thermal conductivity of only 0.2 W/(m⋅K). The composites of silicone rubber are popularly applied, whose thermal conductivity can be increased by an order of magnitude.^[5–8] Previous reports on the improvement of their thermal conductivity have shown that the processing method, formulas, sizes, and surface treatments of the doped particles contribute to the thermal conductivity. Higher amount of filler^[5,9,10] and moderately larger particle size^{[6,7,11–13]} are beneficial for higher thermal conductivity. Different types of fillers^[9,14–16] and different manufacturing procedures^[9,17,18] have a great influence on the thermal conductivity. However, the reported researches on improving the thermal conductivity of silicone rubber are mainly on the doped silicone rubber, few researches are about the structure of the un-doped silicone rubber,^[18] which is important too.

The main structure factors affecting the thermal conductivity of the un-doped silicone rubber include the silicone chain orientation and relative molecular mass. In this paper, non-equilibrium molecular dynamics (NEMD) simulation is used to study these factors. At present, there are few studies on the thermal conductivity of silicone rubber by using molecular dynamics simulation (MDS). Previous studies carried out by Luo et al.^[19] (2011) investigated the thermal conductivity of single-chain, double-chain, and crystalline silicone-oxygen chain. However, there exist some queries in the paper that are worthy of further discussion. Firstly, the effective cross-section area used was not appropriate. According to the definition,^[20] the effective cross-section area of a single chain should be 54 Ų, not 27 Ų. Fourier’s law tells us that if the cross-sectional area is underestimated, the calculated thermal conductivity will be greater than its actual value. Secondly, the density quoted by the authors was 0.92 g/cm³ that was different from the original document^[21] of 0.97 g/cm³. If the density is underestimated, the number of atoms in the same volume decreases, the heat capacity per unit volume will decrease, and the thermal conductivity thus obtained will be lower than its actual value (detailed discussion in Subsection 3.4). Thirdly, the thermal conductivity that the author compared with should be 0.168 W/(m⋅K), not 0.15 W/(m⋅K). Therefore, further study on the thermal conductivity of silicone rubber is necessary.

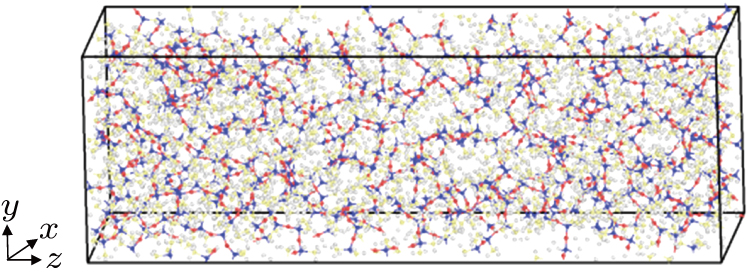
Considering the instability and the very limited application scenarios of a single-chain in practical applications, as well as inspired by the works of Cao et al.^[22] and Xu et al.,^[23] we investigate the crystalline silicone rubber. A crystalline silicone rubber model with the same density as experiment is constructed, and then the thermal conductivity is calculated by NEMD simulation to study the effect of the chain length. Amorphous silicone rubber is also calculated and compared with crystalline silicone rubber to demonstrate the effect of orientation on the thermal conductivity.

MDS can be roughly divided into two types,^[24] equilibrium molecular dynamics (EMD) and NEMD. For NEMD, it is essential to set up a steady temperature gradient in the system, then Fourier’s law is used to obtain the thermal conductivity by calculating heat flow and temperature gradient. There are two kinds of commonly used NEMD methods.^[25] One is to establish a temperature distribution and then calculate the heat flux, such as the dual-thermostat method.^[26] The other is to apply a heat flux to get a temperature distribution, which is called inverse NEMD. A typical one is the Müller–Plathe method.^[27,28]

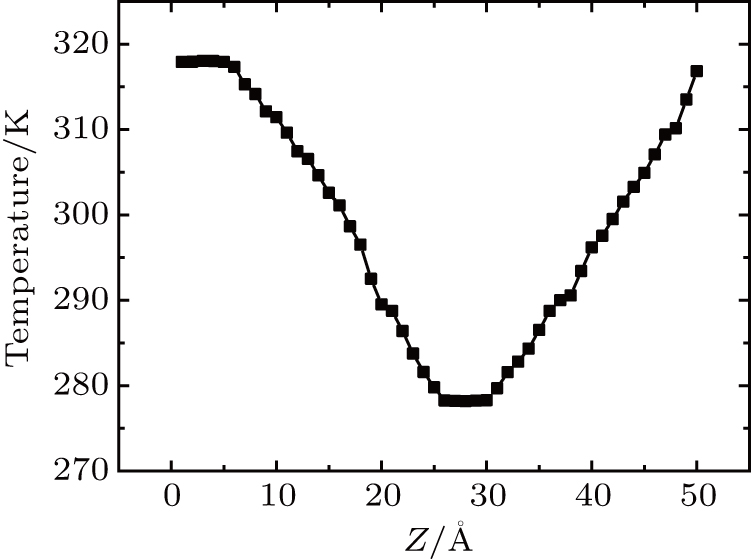
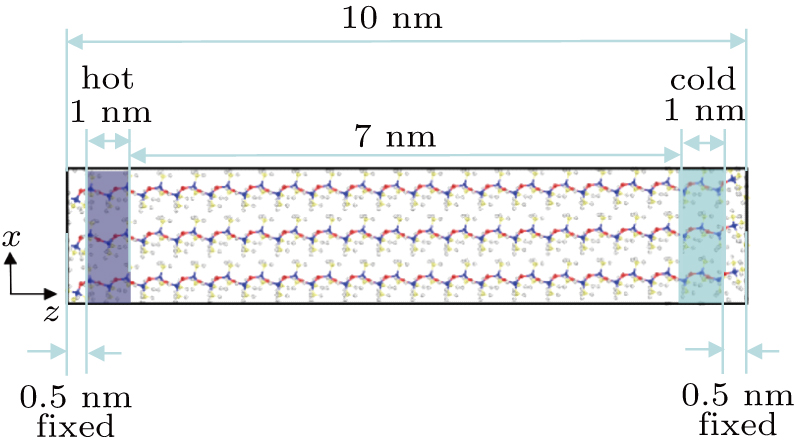
In this paper, the dual-thermostat NEMD method^[29,30] is adopted to calculate the thermal conductivity of silicone rubber. The boundary condition is the thermal bath boundary, so that one end of the model is at high temperature and the other end is at low temperature, and the two ends are named as hot and cold regions, respectively. The energy entering the hot region and the energy leaving the cold region are averaged to obtain the heat flux. The system is divided into 40–50 slices. There are more slices when the length of the simulation system is longer. The temperature of each slice along the heat flux direction is calculated and plotted to obtain the temperature gradient. Then Fourier’s law is used to get the thermal conductivity

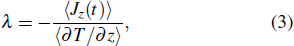
Firstly, a silicone-oxygen monomer [–(Si(CH₃)₂–O)₂–] (as shown in Fig. 1(a)) is built based on the bond length and angle, the main components of both silicone rubber and silicone oil are silicone-oxygen chain polymers. A monomer consists of two silicon atoms, two oxygen atoms, and four methyl fragments, whose mass is 148 (2 × 28 + 2 × 16 + 4 × 15 = 148). Annealing and energy minimization operations are performed on the monomer in Materials Studio (MS) software. The monomer length in the chain direction is 5.0 Å. Then the monomer is duplicated in the Visualizer Module of MS software, chains with different lengths are obtained and the end group of the chains is set to be methyl. The established crystalline structure (as shown in Fig. 1(b)) and amorphous structure (as shown in Fig. 1(c)) have a density of 0.963 g/cm³.^[21] In the process of modeling, the COMPASS force field is set up in Forcite Plus Module in MS. The COMPASS^{[15,19,31–34]} force field is obtained by fitting and correcting the first-principles calculation data with the experimental measurement results, which is of high accuracy. Smart Minimizer is applied in Forcite Plus Module in MS with the convergence level set as ultra-fine to optimize the energy of the initial model, and then the model is transformed into a data file that could be read by LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)^[35] software. Next, annealing operation is carried out, which is 10 heating durations from 300 K to 1000 K, running 200000 steps, followed by 10 cooling durations from 1000 K to 300 K. The temperature of 1000 K allows the particles to have sufficient energy to cross the potential barrier and form a global optimal structure. The silicone-oxygen chain would not crack at this temperature since the chemical reaction is not set in the calculation. The temperature of the stable structure in NVE (micro-canonical) ensemble is calculated with the time steps of 0.4 fs, 0.25 fs, 0.1 fs, and 0.05 fs respectively. Discontinuity of energy integration in the NVE ensemble is found when the time step is too large, which may be caused by fast vibrating hydrogen atoms in the silicone-oxygen chain. Therefore, the time step is set to be 0.05 fs. The non-bond cutoff distance and Coulomb force cutoff distance are 9.5 Å (for large cross-sectional area of amorphous states, 12.5 Å). The particle-particle-particle-mesh (PPPM)^[36] algorithm is set in the calculation to correct the error caused by the cutoff distance. Sufficient NVT (canonical ensemble) simulation is applied without thermostat to relax the structure. To obtain the thermal conductivity, the NEMD method is applied in the NVE ensemble simulation with two Langevin thermostats^[37,38] of cold and hot regions, respectively. When the heat flux and temperature distribution are stable, the thermal conductivity is calculated.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Model of the materials. (a) Monomer structure of silicone oxygen chain, (b) crystalline silicone rubber, (c) amorphous silicone rubber.

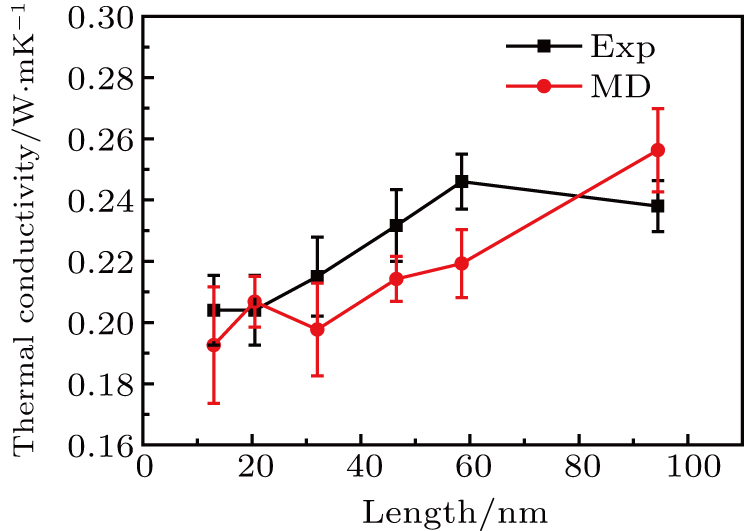
Since ideal crystalline state is difficult to prepare in experiment, and the thermal conductivity data of amorphous silicone rubber in literature^[21] lacks corresponding relative molecular mass, a direct comparison is made between the calculation value and the experimental value of the amorphous silicone rubber that had exact relative molecular mass. It is difficult to directly determine the length of the molecular chain of the polymer. Its length is calculated according to the relative molecular mass of the polymer, the mass of a monomer and its length. The silicone oil used in the experiment is from Dow Corning Company as shown in Table 1.^[39] In order to verify the accuracy of the method, a long silicone-oxygen chain of 26 monomers with methyl as end group is created. It corresponds to a relative molecular mass 3848 (148 × 26 = 3848) that is very close to that of the silicone oil with viscosity of 50 mPa⋅s (the relative molecular mass of 3800 in Table 1). Then, a computing system of size 30.0 Å×30.0 Å×90.0 Å (as shown in Fig. 2) is created. The calculated thermal conductivity of the silicone rubber with a viscosity of 50 mPa⋅s is 0.195 W/(m⋅K). The calculated thermal conductivity of a larger computing system of 36.5 Å×36.5 Å × 120.0 Å is 0.196 W/(m⋅K), showing no difference with this size. The calculation results are almost the same as the average value of 0.204 W/(m⋅K) measured by the second author of this paper within the uncertainty range. The temperature distribution as shown in Fig. 3 is of good linearity, which also indicates the correctness of the simulation method.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Amorphous silicone rubber.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Temperature profile.

Table 1.

Table 1.

Table 1. Relationship between viscosity and relative molecular mass. . Viscosity/mPa⋅s[39] 50 100 200 350 500 1000 Relative molecular mass/g⋅mol−1[40] 3800 6000 9400 13700 17300 28000 Number of monomer 26 41 64 93 117 189 Chain length/nm 13.0 20.5 32.0 46.5 58.5 94.5

Table 1. Relationship between viscosity and relative molecular mass. .

3.1. Effect of chain length on the thermal conductivity of crystalline silicone rubber

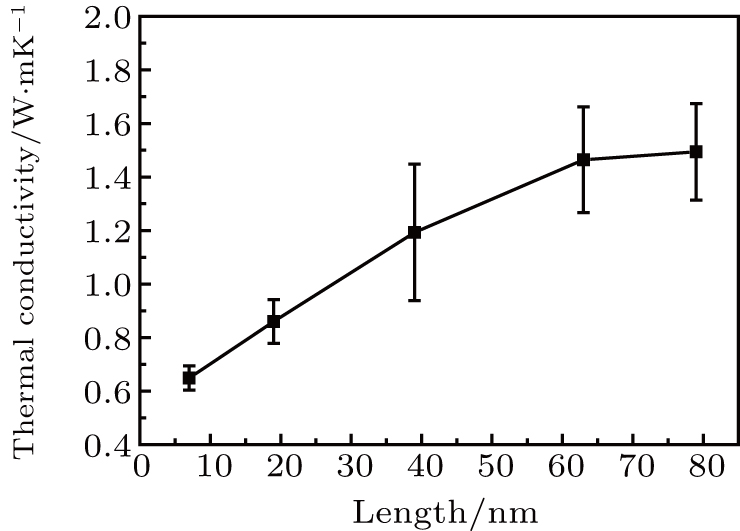
The crystalline silicone rubbers with lengths of 10 nm, 25 nm, 50 nm, 80 nm, and 100 nm in heat flux direction are simulated. The length includes that used to fix the atom to form an adiabatic wall and the length used to control the temperature of the cold and hot regions. The remaining is the length of the temperature gradient, as shown in Fig. 4, which are 7 nm, 19 nm, 39 nm, 63 nm, and 79 nm, respectively in Fig. 5. The cross-sectional area of the simulation system is 21 Å × 21 Å and contains nine chains. The boundaries are fixed at both ends as shown in Fig. 4. Figure 5 is the result of the variation of the thermal conductivity with the chain length. It increases with the chain length of the crystalline structure. When the chain length is 79 nm, the thermal conductivity can reach 1.49 W/(m⋅K) that is about seven times as that of amorphous silicone rubber. The thermal conductivity increases apparently in the length range from 7 nm to 79 nm. The variation of thermal conductivity with chain length could be explained by the finite size effect, which is consistent with the results in the literature.^[41–43] The finite size effect is that when the simulated size L_z is not sufficiently large relative to the phonon mean free path (MFP), the thermal conductivity is limited by the size.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Crystalline structure with length of 10 nm.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Effect of the chain length on the thermal conductivity of crystalline structure.

3.2. Effect of chain length on the thermal conductivity of amorphous silicone rubber

It is clear that the thermal conductivity of the crystalline structure with aligned chains increases with the chain length, but whether there is a similar phenomenon in amorphous state is not known. The latter is investigated by combining experimental measurement and MD simulation. Since the sample to be measured is liquid, a TIM thermal performance measurement instrument (LW-9389, Longwin, Taiwan, China) equipped with a container for liquid testing is used to measure the thermal conductivity of the samples. The container is a plastic one specially designed to prevent heat exchange between sample and surroundings. There is a square hole in the middle of the container in which the sample is filled and directly contacts with the hot and cold meter bars. The scheme of the experiment device to measure the thermal conductivity is shown in Fig. S1 (detailed information in the supporting information). Silicone oil used in the experiment is from Dow Corning Company whose properties are shown in Table 1. The experimental uncertainty of the measured thermal conductivity in the present work is obtained by several (about 4–5) repeated measurements of the same sample. The results are shown in Fig. 6. In the MDS, amorphous structures with different silicone-oxygen chain lengths of 13.0 nm, 20.5 nm, 32.0 nm, 46.5 nm, 58.5 nm, and 94.5 nm are constructed by using the Amorphous Cell Module of MS software. The model size is 30.2 Å×30.2 Å×90 Å. It is verified that this size would not limit the phonon vibration state. The non-bond cutoff distance and Coulomb force cutoff distance are both 12.5 Å. NEMD is applied to calculate the thermal conductivity. The results are also shown in Fig. 6. The thermal conductivities from the experiment and simulated structures are generally in agreement with each other within the uncertainty range. The difference between the experimental and numerical values comes from the uncertainties of the measurement and MDS. The effect of the chain length on the thermal conductivity is not much in the range of 13.0–94.5 nm. The chain length has much less effect on the thermal conductivity of amorphous silicone rubber, while it has more apparent effect on crystalline silicone rubber. Therefore, it can be concluded that better chain alignment is beneficial to thermal conductivity.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Variation of the thermal conductivity with the chain length for amorphous structure of silicone rubber from experiment and MDS.

3.3. Effect of temperature on the thermal conductivity of silicone rubber

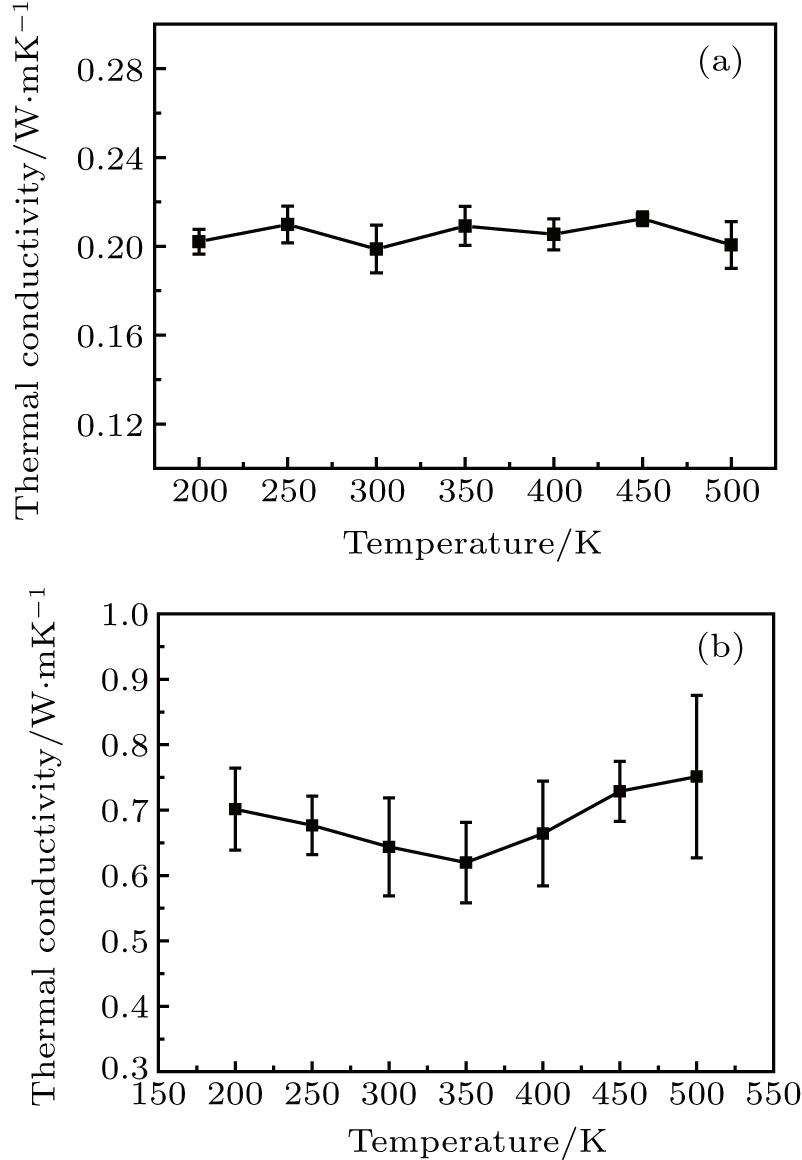
Temperature is also thought to affect the thermal conductivity. Currently, there are few studies on the effect of temperature on thermal conductivity of amorphous silicone rubber. In this paper, the thermal conductivity of silicone rubber both in amorphous state and crystalline state is calculated at different temperatures. The results, as shown in Fig. 7(a), indicate that there is almost no change of thermal conductivity associated with temperature from 200 K to 500 K for amorphous silicone rubber. From the perspective of phonon density of states (DOS) as shown in Fig. 8, the phonon DOS of crystalline silicone rubber is different from that of amorphous silicone rubber. Crystalline silicone rubber has more low frequency phonons than amorphous silicone rubber, therefore the thermal conductivity of crystalline silicone rubber is higher than that of amorphous silicone rubber. In this temperature range, the thermal conductivity of crystalline silicone rubber almost has no dependence on the temperature. This dependence is different from the previous studies of graphene,^[44] where the thermal conductivity of graphene decreases with temperature. For the dielectric crystal, its thermal conductivity increases first at low temperature and then decreases at high temperature. The result of Wei et al.^[44] showed the later part of the temperature dependence. For the non-crystalline materials, the temperature dependence of the thermal conductivity does not always have consistent variation with temperature. For example, the investigations of bulk polycrystalline silicone^[45] and nanocrystalline silicone film^[46] showed that their thermal conductivities had weak or no dependence on temperature in a wide range from 300 K to 900 K because only short range of phonon MFP was allowed. From the research of Wei et al.,^[44] the temperature dependence of thermal conductivity became weak gradually with increasing graphene layers, which was also because long range phonon was limited by its structure. The crystalline state of silicone rubber is not a real crystal, the chains are aligned and fixed at two ends but there are still a lot of fragments that can move within a certain range and the properties of this part are similar to those of the amorphous.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Effect of temperature on thermal conductivity: (a) amorphous state, (b) crystalline state

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Phonon DOS in crystalline and amorphous state: (a) silicon atoms, (b) oxygen atoms.

NEMD method is used to study the effect of chain length on the thermal conductivity of crystalline silicone rubber and amorphous silicone rubber. It is found that there is an apparent increase in thermal conductivity of crystalline state with the chain length, but the chain length has less effect on thermal conductivity in amorphous state, which indicates that morphology plays an important role in thermal transport. In addition, the thermal conductivities of both amorphous state and crystalline state at different temperatures are calculated. It is observed that in the temperature range from 200 K to 500 K, the temperature has almost no effect on the thermal conductivity. The crystalline state of silicone rubber has larger MFP and shorter conducting path due to its orientation. Therefore, its thermal conductivity is higher than that of amorphous state.