† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11874287 and 11574229), the National Basic Research Program of China (Grant No. 2016YFA0302800), and the Fund from Shanghai Science and Technology Committee, China (Grant No. 18JC1410900).
We study the influence of driving ways on the interaction in a two-atoms cavity quantum electrodynamics system. The results show that driving ways can induce different excitation pathways. We show two kinds of significantly different excitation spectrums under two ways: driving cavity and driving atoms. We demonstrate that driving atoms can be considered as a method to obtain the position information of atoms. This research has very practical application values on obtaining the position information of atoms in a cavity.
Cavity quantum electrodynamics (QED) provides a platform to explore the quantum effects of light--matter interaction.[1–3] In strong-coupling regime, due to the atom–field interaction overwhelms dissipation of the system, cavity QED realizes the coherent exchange of a single photon energy between the atom and cavity. This quantum interaction progress has been observed in cavity QED experiment.[4–7] And many quantum effects also have been realized in experiments, including non-demolition measurement,[8–14] quantum gates,[15–19] quantum entanglement,[20–23] and manipulation of single atom.[24–27] In addition, non-classical light is also shown in a cavity QED system.[28–34] In their experiments, the non-classical effects, such as the anti-bunching phenomenon and sub-poissonian effect, are demonstrated in their results.
Recently, the two-atoms cavity QED system is widely studied in many articles.[35–45] Agarwal et al. showed a phenomenon in which the radiation can distinctly exceed the free-space superradiant behavior in a two-atoms cavity QED system by driving atoms. They call it hyperradiance.[39] They also found that the light field can be tuned from antibunched to (super-)bunched as well as nonclassical to classical behavior by merely modifying the atomic position.[44] Zhu et al. also proposed a scheme to realize the three-photon blockade. They found that out-of-phase coupling is more efficient to obtain three-photon blockade by driving the atoms.[42] The above works concentrate on the characters of radiation field and they considered only the case of driving atoms. This motivates us to exploring the basic properties in collective system under different driving ways.
In this paper, we consider a system in which two atoms are confined in a single mode cavity. We explore the transmission spectrum of the two-atoms cavity QED system at different radiation phases. Two driving ways, i.e., driving cavity and driving atoms, are considered in our work. Our results demonstrate that the transition paths are significantly influenced by the driving way. And the phase information between two atoms is distinguished only by driving atoms. The results provide a method to measure the position information of atoms and also can guide the experiment to obtain non-classical light.
In our scheme, the atoms–cavity system is described by the following quantum master equations


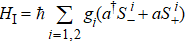


We define γ as the spontaneous emisson rate of the atom in excited state, and ωa is the transition frequency of single two-level atom. In the above Hamiltonian, Δa = ωL – ωa is the atom–laser detuning and Δc = ωL – ωc is the cavity–laser detuning. Atom–cavity coupling strength is gi = g cos(2πzi/λc) associated with the positon of atoms where λc is the wavelength of cavity mode and zi is the position of atom. In Eq. (




We assume the coupling strength g1 = G cos(ϕ1) and g2 = G cos(ϕ2) where the phases are defined as ϕ1 = z1/λc and ϕ2 = z2/λc. Firstly, we consider the situations ϕ2 = ±ϕ1+2nπ, which means the coupling strength of two atoms is equal, g1 = g2 = g. So the relative position information of atoms are measured by the coupling interaction. We also assume ωa = ωc which means Δa = Δc = Δ. Under these conditions, the dressed states pictures of the systems can be easily obtained. The mean photon number 〈a†a〉 is obtained by numerically solving the master equation Eq. (

This phenomenon can be explained easily from the quantum interference and perturbation theory. Under weak driving strength, the photons mainly occupy the single photon state, i.e., 〈a†a〉 ≈ P1 where P1 is the population of state |gg,1〉. The first excited eigen states of HI are expressed as 





To be different from the above cases, we also pay attention to the case at ϕ2 = ±ϕ1 + (2n+1)π. The dressed states structures and some of transition paths are displayed in Figs. 











By comparing Fig.
In Fig.
In summary, we have shown the interaction of a two-atoms collective system by different driving ways. We analyzed the physical transition paths in dressed states presentation. We investigated the differences of the excitation spectrum by driving the cavity and driving the atoms. The results demonstrate that driving the atoms can be used as a measurement method to obtain the relative position information of the two atoms. This measurement only needs to analyze transmission spectrum. This study has very practical application values on achieving the measurement of atom position and provides a train of thought to study the interaction progress in a cavity QED system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |






