† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11834003, 91536218, 11034002, 11274114, 11504112, and 11874151), the National Key Basic Research and Development Program of China (Grant No. 2011CB921602), the Fundamental Research Funds for the Central Universities, China, Shanghai Pujiang Talents Plan, China (Grant No. 18PJ1403100), and Exploration Funds from the Shanghai Natural Science Foundation, China (Grant No. 18ZR1412700).
Two novel electrostatic traps named octopole-based disk electrostatic trap (ODET) and tubular-based disk electrostatic trap (TDET) are proposed for trapping cold polar molecules in low-field-seeking states. Using MgF as the target molecule, single loading and multi-loading methods are numerically simulated with varied incident velocities of slow molecular beams in the two types of traps, respectively. In ODET, with an incident velocity of 10 m/s, a highest loading efficiency of 78.4% or 99.9% has been achieved under the single loading or multi-loading operation mode. In TDET, with an incident velocity of 11 m/s, a highest loading efficiency of 81.6% or 106.5% has been achieved using the two loading methods, respectively. With such high loading efficiencies, the trapped cold molecules can be applied in the researches of cold collisions, high precision spectroscopy, and precision measurements. Especially, together with a blue-detuned hollow beam, the new electrostatic traps proposed here offer a new platform for the following gradient-intensity cooling of MgF molecules, which may provide a new way to produce high density ultracold molecules.
Research on cold molecules is progressing rapidly, which offers unique possibilities for the investigation of new physical phenomena.[1–3] The trapped cold molecules especially are suitable for or facilitate the study of cold collisions,[4–7] cold chemistry,[8–11] high-resolution spectroscopy,[12,13] and precision measurements,[14–16] benefiting from the longer observation time. A variety of techniques have been developed to trap cold molecules.[17–27] In 1998, Doyle group realized magnetic trapping of calcium monohydride molecules thermalized in helium buffer gas.[28] In the same year, Knize group successfully trapped cesium dimers with an optical trap.[29] In 2000, Meijer group demonstrated electrostatic trapping of ammonia molecules with a trap that composes of two end-caps and a ring electrode in the middle.[30] Thus far, several cold species of interest and highly relevant to science are trapped with electric or magnetic fields, including ND3 molecules,[18–20,22,30] OH radicals,[21,31] metastable CO molecules,[32] and NH radicals,[33–35] which have been used in the studies of direct measurement of the radiative lifetime,[32,36] cold collisions,[37–39] nonadiabatic transitions,[22] Zeeman relaxation,[34] and Sisyphus cooling.[40] Generally, the trap mentioned above is loaded in a single cycle, which obviously limits the number of the trapped molecules and thus the number density. A sufficient number in the trap is absolutely essential for the study of molecular collisions and future applications such as evaporative or sympathetic cooling. In 2001, van de Meerakker et al. proposed a subtle method that works specifically for NH radicals to accumulate the molecules decelerated by a Stark decelerator in a magnetic trap to increase the phase-space density,[41] and it was experimentally demonstrated in 2011.[42] In 2005, Rempe group realized a continuously loading of an electrostatic trap for ND3 molecules from a quadrupole velocity filter, where the trap consists of five ring-shaped electrodes and two spherical electrodes at both ends.[43]
Here, we propose two types of highly efficient electrostatic traps for trapping polar molecules. With the single loading method, the slow molecules are loaded in one cycle, during which the trap potential is kept switching on. With the multi-loading method, the molecules are loaded in five cycles, and the trap potential requires opening up after each cycle. Throughout the paper, we choose MgF as the target molecule, as it is feasible for laser cooling.[44–46] Furthermore, the electrostatic trapped MgF molecules are anticipated to be used in the gradient-intensity cooling with a blue-detuned hollow beam, which may provide a new approach to produce dense ultracold molecules.
In the following sections, the geometries of the new traps and the electric distributions generated by the electrodes of the traps are presented. In order to verify the loading methods, Monte Carlo simulations are performed for the two types of traps operated with the single loading and the multi-loading methods, respectively. The resulting phase-space distributions and velocity distributions are also given. Some discussion and conclusions are presented at the end.
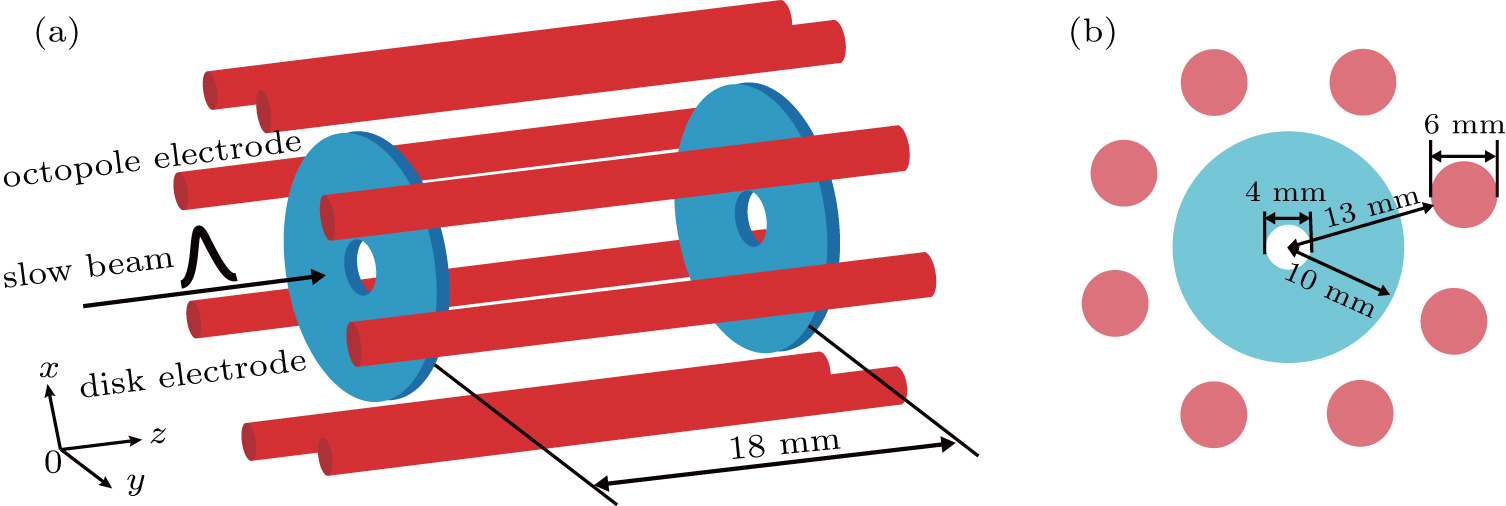
As shown in Fig.
As shown in Fig.
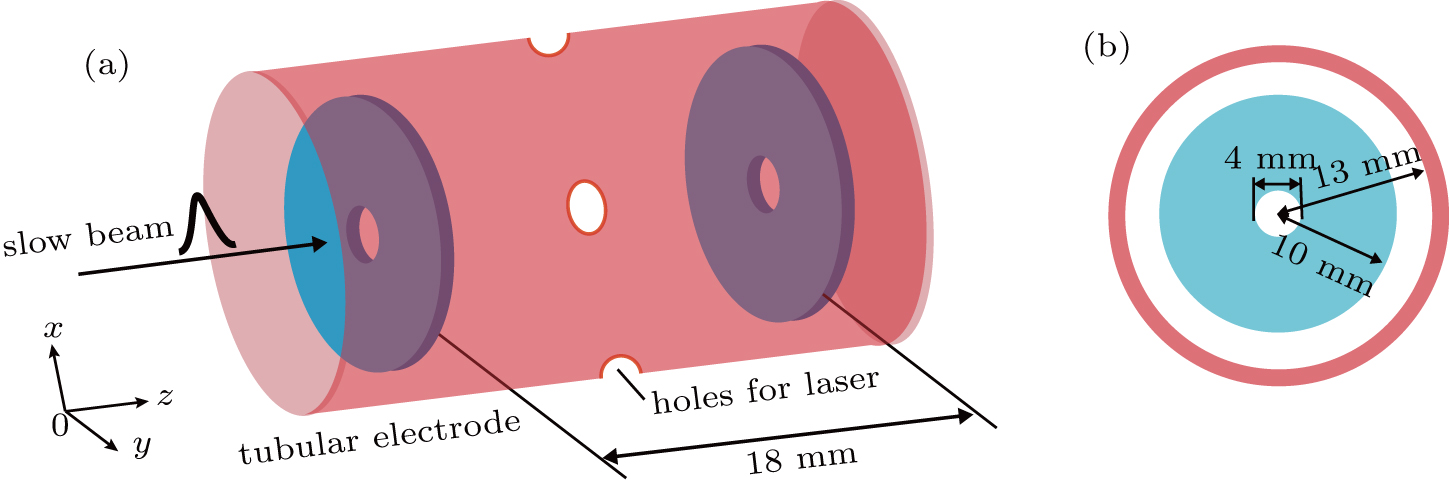
As to the tubular-based disk electrostatic trap (TDET), it has the same disk electrodes in size and layout as those of ODET, and a tubular electrode around, as shown in Fig.
The tubular electrode is 30 mm long and has an inner radius of 13 mm, a thickness of 2 mm. Two pairs of 5-mm-diameter holes are made in the middle part of the tubular electrode for laser detections along the x and y directions, respectively. When applying voltages of 0, +U, and −U to the first disk electrode, the second one, and the tubular electrode, respectively, a loading configuration is formed, as shown in Fig.
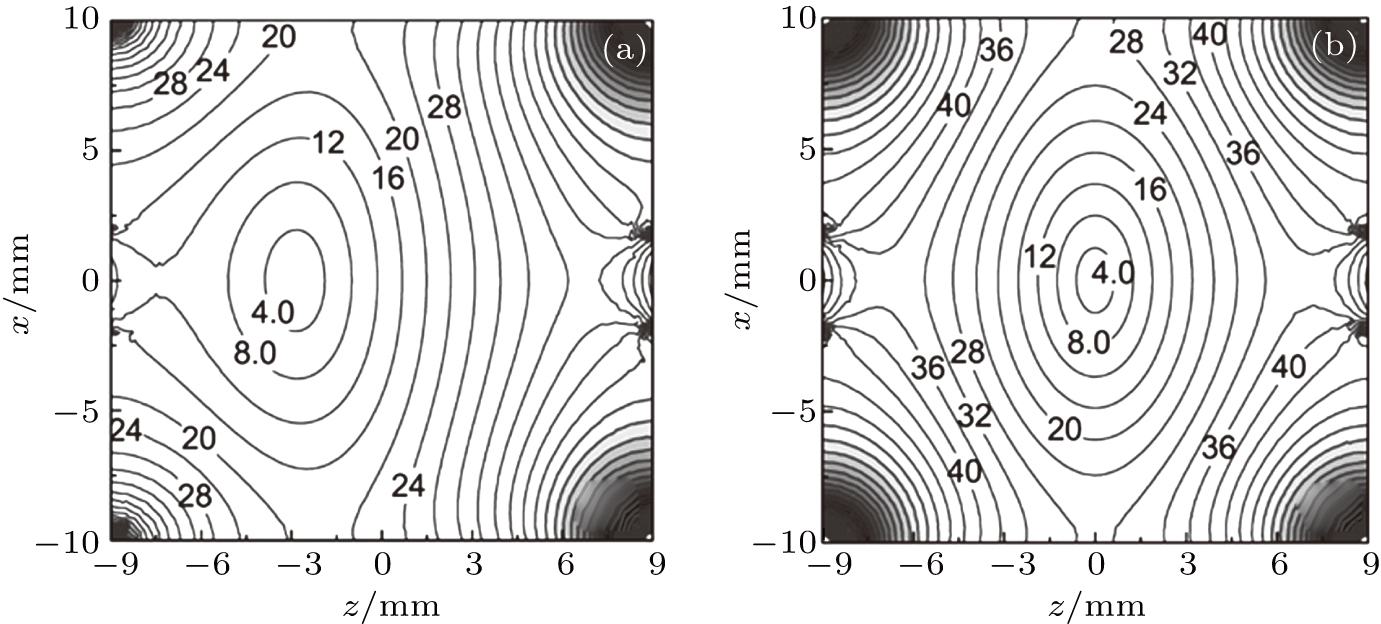
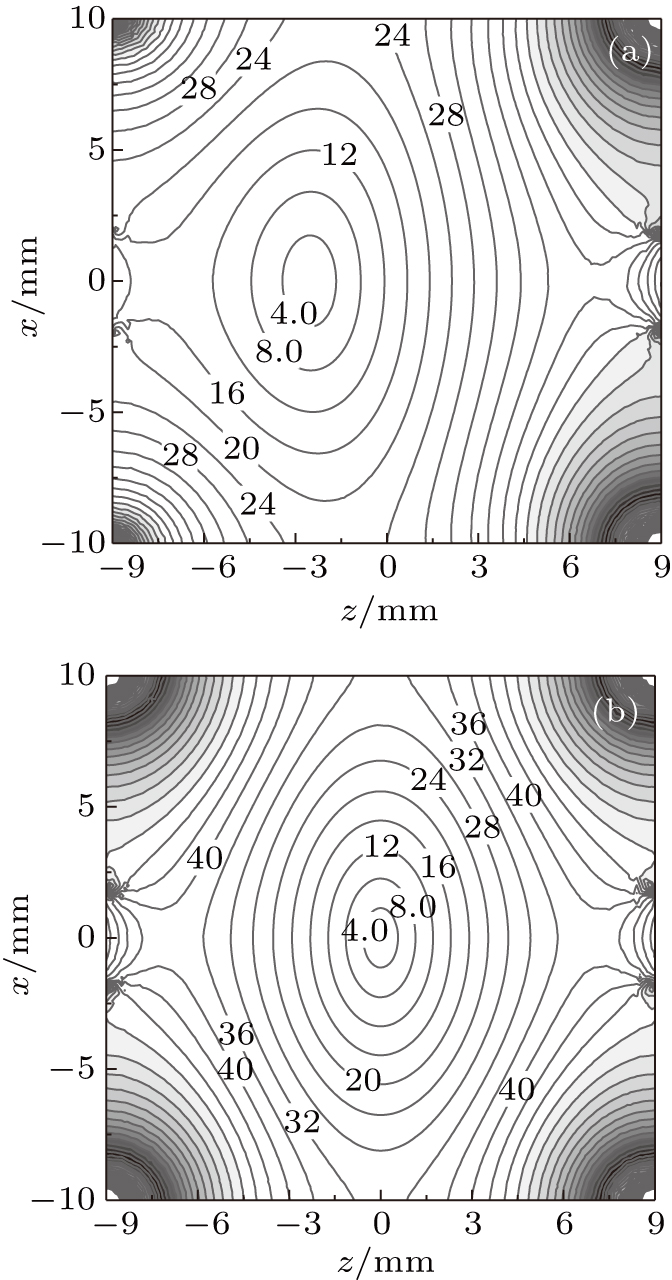
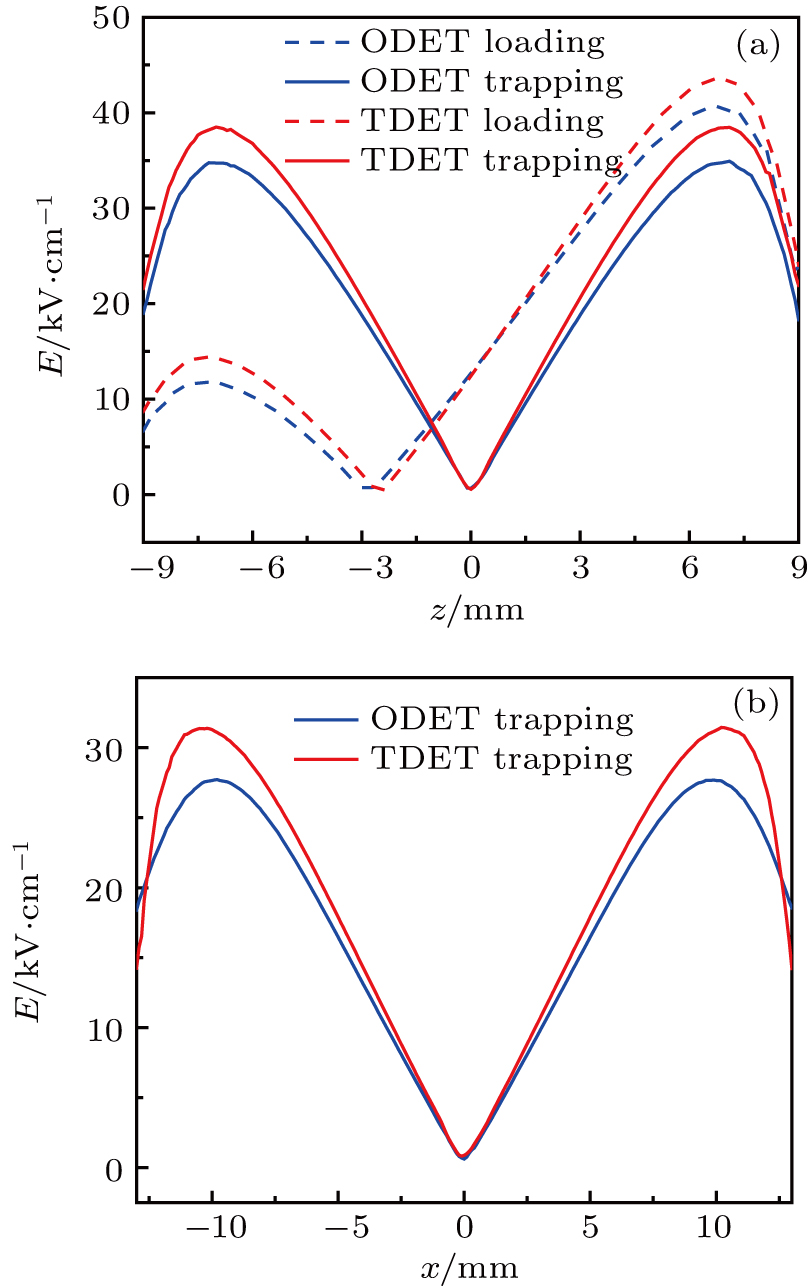
To get a detailed understanding of the two electrostatic traps (ODET and TDET), we calculate the electric field distributions along the z direction, i.e., the longitudinal direction, and the x direction, i.e., the transverse direction, under the loading and the trapping configurations with U = 26 kV, respectively. As shown in Fig.
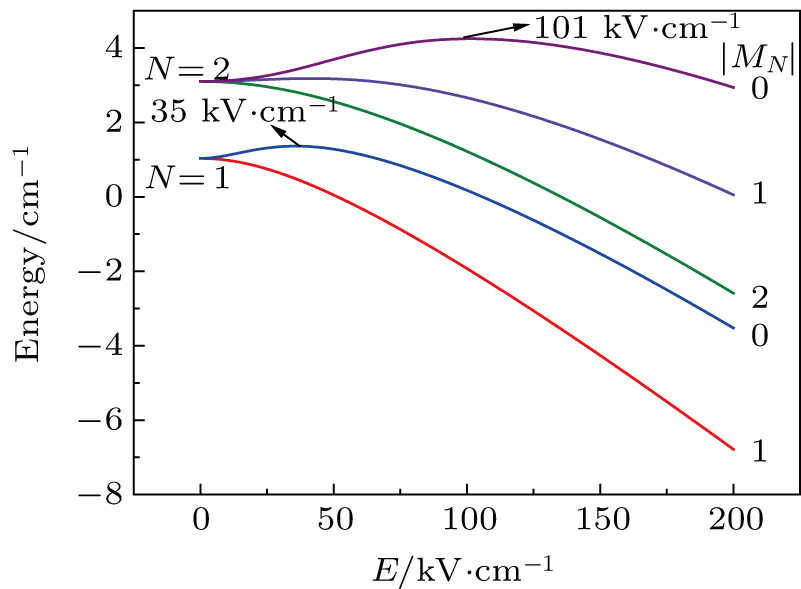
The slow MgF molecular beam with tunable central velocities can be achieved using a Stark decelerator.[48–51] Because the rotational temperature of the molecular beam after the supersonic expansion is usually several Kelvins and most of the molecules reside in the lowest rotational states, the Stark shifts of MgF molecules in the lowest rotational states are calculated, as shown in Fig.
The dipolar force exerted on the dipolar molecule arises from the interaction between the molecular dipole moment and the applied electric field, which is the so called Stark effect. The dipolar force can be expressed as
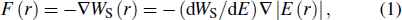
In the numerical simulations, the selected molecule from the decelerated MgF molecular beam flies into the trap through the hole of the first disk electrode in the absence of the electric field. Once the molecule arrives at the minimal electric field under the loading configuration, the trap is switched into the loading configuration. Then, the molecule starts to climb up the potential and is decelerated by the repulsive dipolar force. When the molecule is slowed to astandstill, the trap is switched into the trapping configuration, and then the molecule is confined in the trap. In this paper, we assume that the voltage applied to the trap is U = 26 kV and the incident pulsed MgF molecular beam has Gaussian distributions both in the spatial and velocity coordinates. The full widths at half maximum (FWHM) of the spatial and the velocity distributions in the x, y, and z directions are 4 mm, 4 mm, 6 mm and 5 m/s, 5 m/s, 6.5 m/s, respectively. The molecular number of one pulsed slow beam is 105. In addition, the elastic collisions are neglected in the simulations, because the density of the trapped molecules is not too high to lead to many collisions.
Using the single loading method, the trap is loaded with one pulsed molecular beam and the trapping configuration is kept till the end. The calculated trap loading efficiency is defined as the fraction of the one pulsed incident molecules, 105, and the molecules that are confined in the trap for 40 ms after the trapping configuration has been switched on. In Fig.
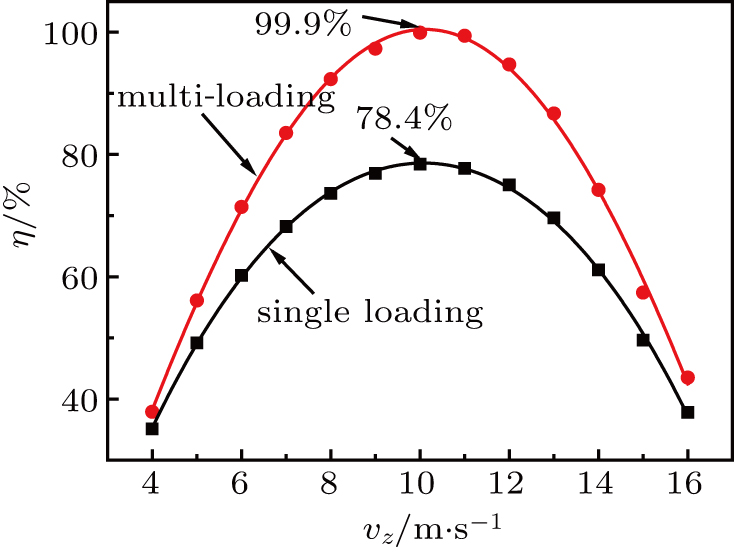 | Fig. 7. Dependences of the loading efficiency of the ODET for MgF molecules on the incident velocity of the slow beam under the single loading and the multi-loading operation modes, respectively. |
With the multi-loading method, the trap is loaded with the first pulsed molecular beam under the loading configuration and switched into the trapping configuration upon finishing the loading process. Then, the trapping configuration is kept till the beginning of the loading and trapping for the second pulse. The duration of one loading and trapping cycle is 100 ms. When loading the second pulse, the trap requires opening up and switching back into the loading configuration, followed by the trapping process. In all, the processes repeat five times for five pulsed molecular beams. The loading efficiency is defined as the ratio of the molecules confined in the trap after the multi-loading to the molecules in one pulsed incident beam.[42] In Fig.
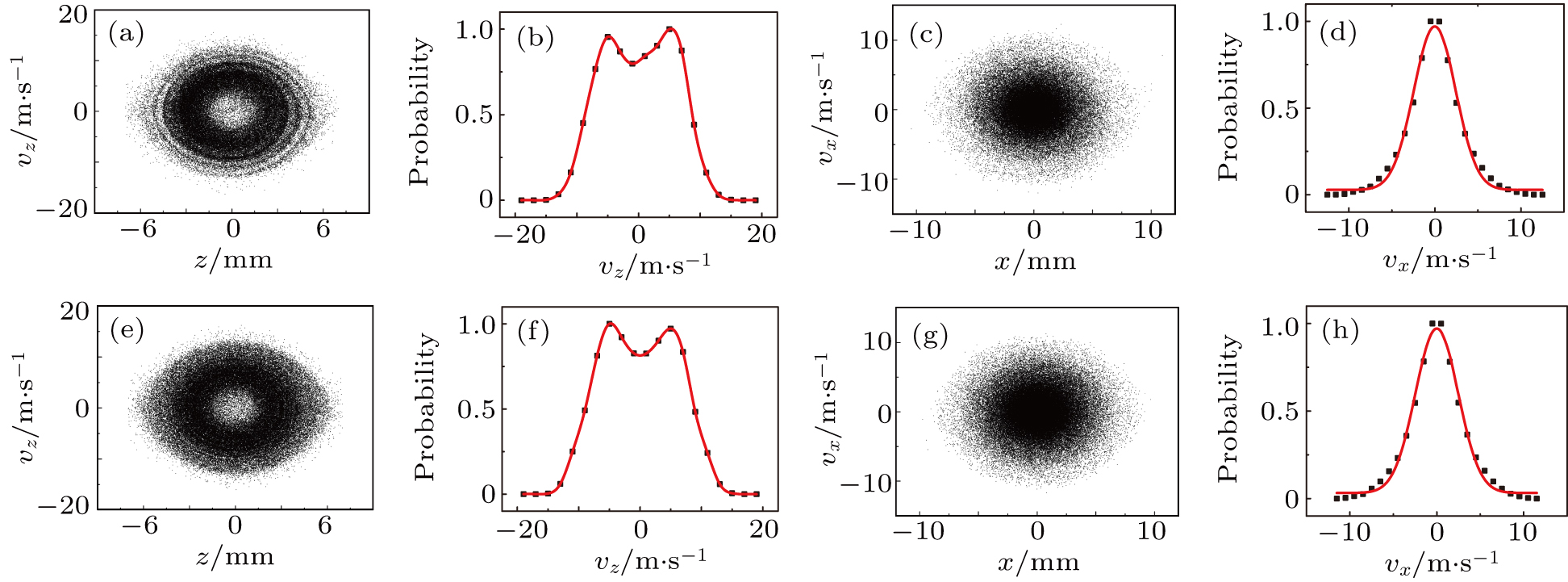
With an incident velocity of 10 m/s in the slow beam, the phase-space distributions and the corresponding velocity distributions are presented, as shown in Fig.
The lower four sets of results in Fig.
Compared with the temperatures of the trapped MgF molecules under the single loading operation mode, the longitudinal temperature under the multi-loading operation mode increases by about 12%, still on the same order of magnitude, and the transverse temperature remains unchanged.
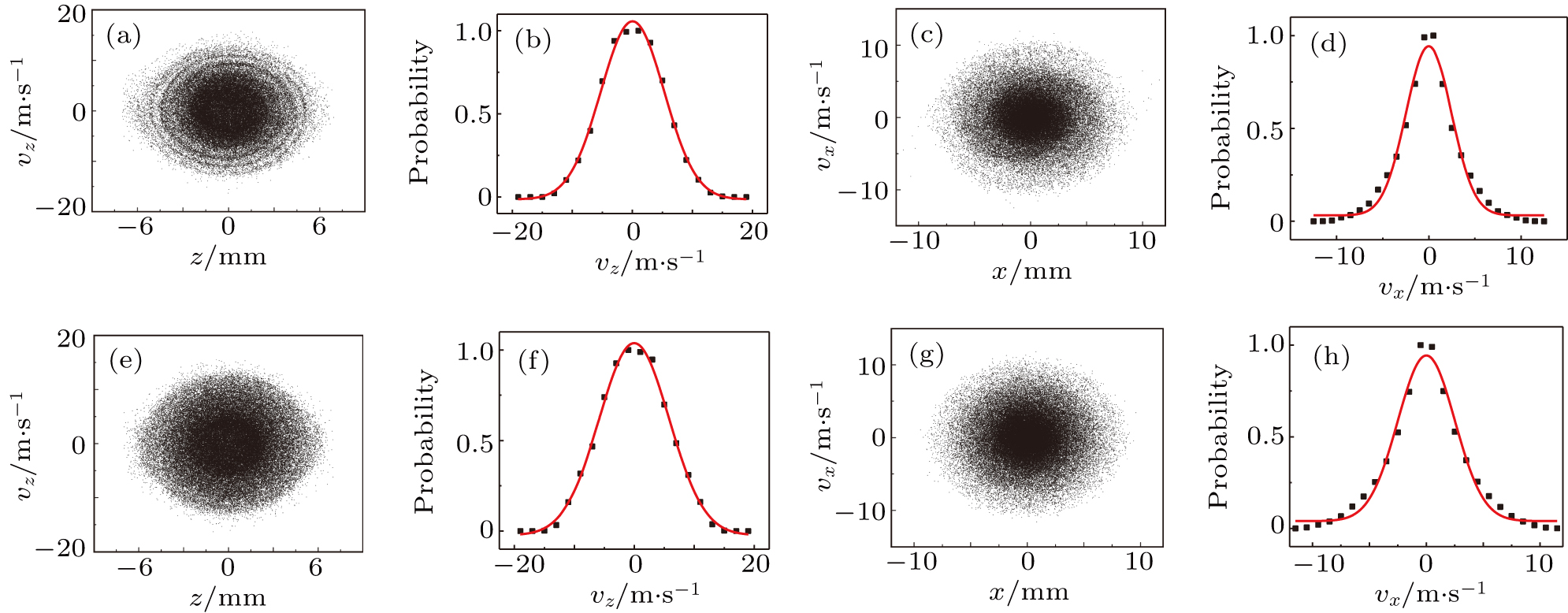
With an incident velocity of 7 m/s in the slow beam, the phase-space distributions and the corresponding velocity distributions are presented in Fig.
In Fig.
The definition of the loading efficiency of TDET is the same as that for ODET in Subsection
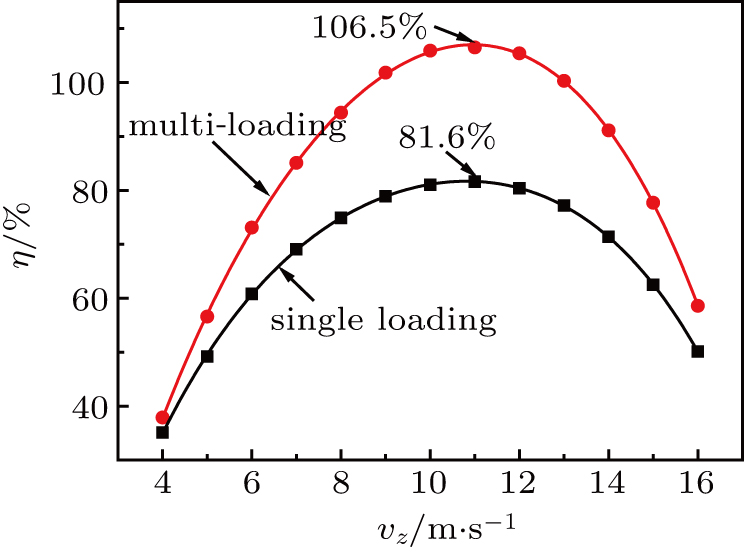 | Fig. 10. Dependences of the loading efficiency of the TDET for MgF molecules on the incident velocity of the beam under the single loading and the multi-loading operation modes, respectively. |
Under the single loading or multi-loading operation mode, the phase-space distributions and the corresponding velocity distributions of the trapped MgF molecules in TDET are similar to those in ODET. When the highest loading efficiency is achieved, the FWHMs of the longitudinal velocity distributions of the trapped molecules in TDET are both about 1.4 times the FWHMs obtained in ODET, under the single loading and the multi-loading operation modes, respectively; the FWHM of the transverse velocity distribution in TDET is nearly the same as that in ODET.
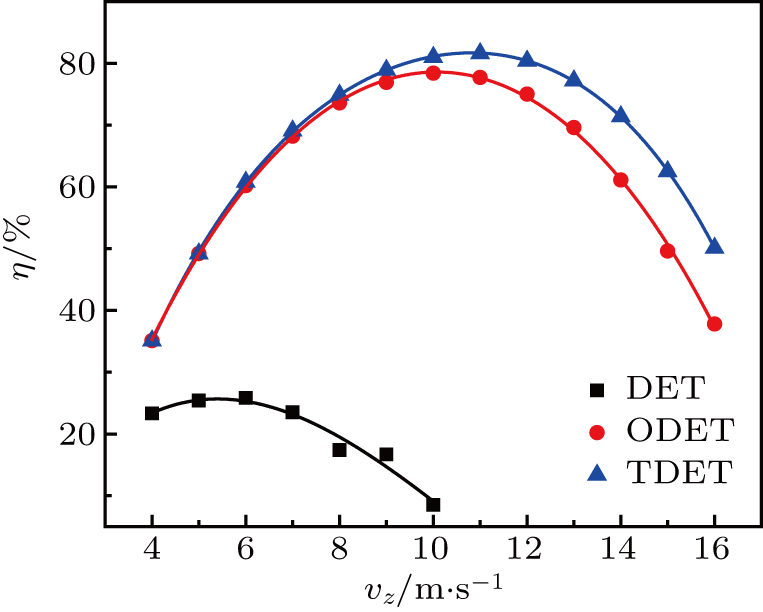
Compared with the disk electrostatic trap (DET) in Ref. [27], the ODET and TDET proposed here achieve a significant improvement in the trap loading efficiency. Using MgF as the target molecule, the dependences of the trap loading efficiencies of DET, ODET, and TDET on the incident velocity of the slow beam under the single loading operation mode are calculated, respectively, as shown in Fig.
We have proposed two new electrostatic traps with simple construction and high loading efficiencies for cold polar molecules in LFS states. Under the trapping configuration, the voltage on the octopole electrodes of ODET or the tubular electrode of TDET significantly increases the transverse trap depth and effectively avoids the losses of molecules. This leads to a very high loading efficiency for each of the new traps. The multi-loading method proposed here is a simple versatile reloading method applicable for pulsed polar molecular packets of different species and explored with Monte Carlo simulations. With MgF as the target molecule, in ODET a highest loading efficiency of 78.4% or 99.9% has been achieved under the single loading operation or the multi-loading operation mode, and a highest loading efficiency of 81.6% or 106.5% has been achieved in TDET. The new electrostatic traps offer good early-stage preparations for the following gradient-intensity cooling of MgF molecules with a blue-detuned hollow beam, which may provide a new approach to produce dense ultracold molecules.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] |