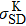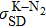† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2016YFA0301500), the National Natural Science Foundation of China (Grant No. 61835013), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant Nos. XDB01020300 and XDB21030300).
The hybrid optical pumping spin exchange relaxation free (HOPSERF) atomic co-magnetometers make ultrahigh sensitivity measurement of inertia achievable. The wall relaxation rate has a big effect on the polarization and fundamental sensitivity for the co-magnetometer, but it is often neglected in the experiments. However, there is almost no work about the systematic analysis of the influence factors on the polarization and the fundamental sensitivity of the HOPSERF co-magnetometers. Here we systematically study the polarization and the fundamental sensitivity of 39K–85Rb–21Ne and 133Cs–85Rb–21Ne HOPSERF co-magnetometers with low polarization limit and the wall relaxation rate. The 21Ne number density, the power density and wavelength of pump beam will affect the polarization greatly by affecting the pumping rate of the pump beam. We obtain a general formula on the fundamental sensitivity of the HOPSERF co-magnetometers due to shot-noise and the fundamental sensitivity changes with multiple systemic parameters, where the suitable number density of buffer gas and quench gas make the fundamental sensitivity highest. The fundamental sensitivity 7.5355×10–11 rad·s–1·Hz–1/2 of 133Cs–85Rb–21Ne co-magnetometer is higher than the ultimate theoretical sensitivity 2×10–10 rad·s–1·Hz–1/2 of K–21Ne co-magnetometer.
In recent years, ultrahigh sensitive co-magnetometers have become a hotspot in research of inertial navigation, geophysics,[1,2] gravitational wave detection,[3] downhole orientation sensing[4] and general relativity test.[5] Ring laser gyroscopes and fiber optic gyroscopes based on the Sagnac effect are widely used in sea and space navigation.[6] With the rapid development of quantum physics, the spin exchange relaxation free (SERF) atomic spin co-magnetometer[7] uses hyperpolarized nuclear spins to sense rotation. Atomic co-magnetometers[8,9] use two or more spin species with different gyromagnetic ratios occupying the same volume to cancel the sensitivity of the co-magnetometers to random changing magnetic field and this leaves them only sensitive to rotation or other fields. Atomic co-magnetometers are also used to search violation of local Lorentz invariance,[10,11] to study spin-dependent forces[12–15] and to search electric dipole moments.[16] A SERF atomic co-magnetometer based on K–3He[17] reached rotation sensitivity of 5 × 10–7 rad·s–1·Hz–1/2 in 2005. A Cs–129Xe co-magnetometer was also studied.[18] Due to the formation of van der Waals molecules between Cs and 129Xe,[19] the Cs relaxation rate is much larger than that of the Rb in a Rb–21Ne pair. A K–Rb–21Ne co-magnetometer ensures high sensitivity for rotation sensing. Theoretical analysis shows that the fundamental rotation sensitivity[17] of a K–21Ne atomic co-magnetometer could reach 2 × 10–10 rad·s–1·Hz–1/2 with 10 cm3 sense volume as the density of K is 1 × 1014 cm–3, the number density of buffer gas 21Ne is 6 × 1019 cm–3. A dual-axis K–Rb–21Ne comagnetometer can suppress the cross-talk effect and carry out high-precision rotation sensing along two sensitive axes simultaneously and independently[20] and a parametrically modulated dual-axis Cs–Rb–Ne atomic spin gyroscope can effectively suppress low frequency drift and achieve a bias instability of less than 0.05 deg/h.[21] The synchronous measurements of inertial rotation and magnetic field in a K–Rb–21Ne comagnetometer based on the nuclear spin magnetization of the 21Ne self-compensation magnetic field and enhancement of the rotation signal[22] and the real-time closed-loop control of the compensation point[23] in a K–Rb–21Ne comagnetometer become the focus of research for rotation sensing.
In this paper, we study the polarization and fundamental sensitivity of the HOPSERF co-magnetometer taking the wall relaxation rate into account, which has a big effect on the polarization and fundamental sensitivity, but usually it is neglected in the experiments. We obtain a general formula on the fundamental sensitivity with a low polarization limit, which describes the fundamental sensitivity of the co-magnetometer changing with the number density of buffer gas and quench gas, wavelength of pump beam, mole fraction of 85Rb, power density of pump beam, external magnetic field, cell effective radius (the shape of the cell is roughly spherical), measurement volume and cell temperature. We have investigated 39K–85Rb–21Ne and 133Cs–85Rb–21Ne HOPSERF atomic magnetometers (39K (133Cs)–85Rb–21Ne co-magnetometers), then found that the fundamental sensitivity of 133Cs–85Rb–21Ne co-magnetometer is higher than the 39K–85Rb–21Ne co-magnetometer at the same cell temperature in the SERF regime with the same frequency detuning of a pump beam when (1) the external magnetic field is smaller than about 1.7884 × 10–8 T, (2) the mole fraction of 85Rb is larger than about a critical value 0.9662, or (3) the power density of the pump beam is smaller than about 0.229 W/cm2 under our chosen conditions. Optimizing the co-magnetometer parameters is advantageous to improve the sensitivity of the co-magnetometer in measuring weak rotation signal.
Furthermore, we obtain a higher fundamental sensitivity of about 7.5355 × 10–11 rad·s–1·Hz–1/2 with 133Cs–85Rb–21Ne co-magnetometer when (1) the polarization of 85Rb atom is about 8.193 × 10–4, (2) the measurement time is 1 s, cell temperature is 406.696 K, (3) the number density of Rb is about 1 × 1014 cm–3, (4) cell effective radius a = 2 cm, measurement volume is 10 cm3, (5) external magnetic field B = 1 × 10–12 T, (6) the number density of quench gas N2 is 6.3 × 1018 cm–3, and (7) the number density of buffer gas 21Ne is 6 × 1019 cm–3, and the fundamental sensitivity is higher than the fundamental rotation sensitivity[17] of a K–21Ne atomic co-magnetometer of 2 × 10–10 rad·s–1·Hz–1/2. These findings not only optimize the parameters for the SERF regime, but also provide an experimental guide for design of SERF co-magnetometers.
The SERF atomic co-magnetometers have some properties similar to the SERF atomic magnetometers. As we discussed in our previous work,[24] we take the alkali metal vapor cell (the shape of the cell is roughly spherical) of the SERF atomic co-magnetometers based on HOP containing two types of alkali metal atoms, 39K–85Rb or 133Cs–85Rb, we take 39K or 133Cs as atom A, select 85Rb as atom B in the SERF regime,[24,25] 21Ne as buffer gas to suppress the spin relaxation and N2 as quench gas to restrain radiative de-excitation of alkali metal atoms.[26] The saturated density[27] of the alkali-metal atoms vapor in units of cm–3 at cell temperature T in Kelvin is 

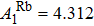




Considering the spin exchange between alkali-metal atoms A and B in the hybrid vapor cell, we assume that the vapor densities obey Raoult’s law,[30] 



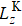




The full Bloch equations are given as follows:[34,35]

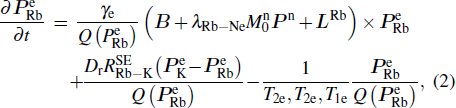
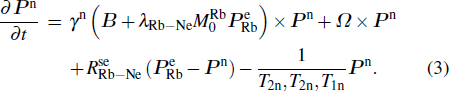

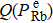
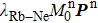

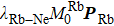



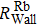
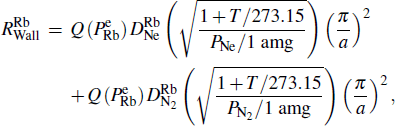

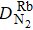

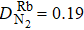


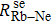


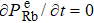

We can find that the relaxation rates for diffusion of 85Rb in the 21Ne gas to the wall of 39K–85Rb–21Ne co-magnetometer 

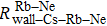

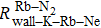







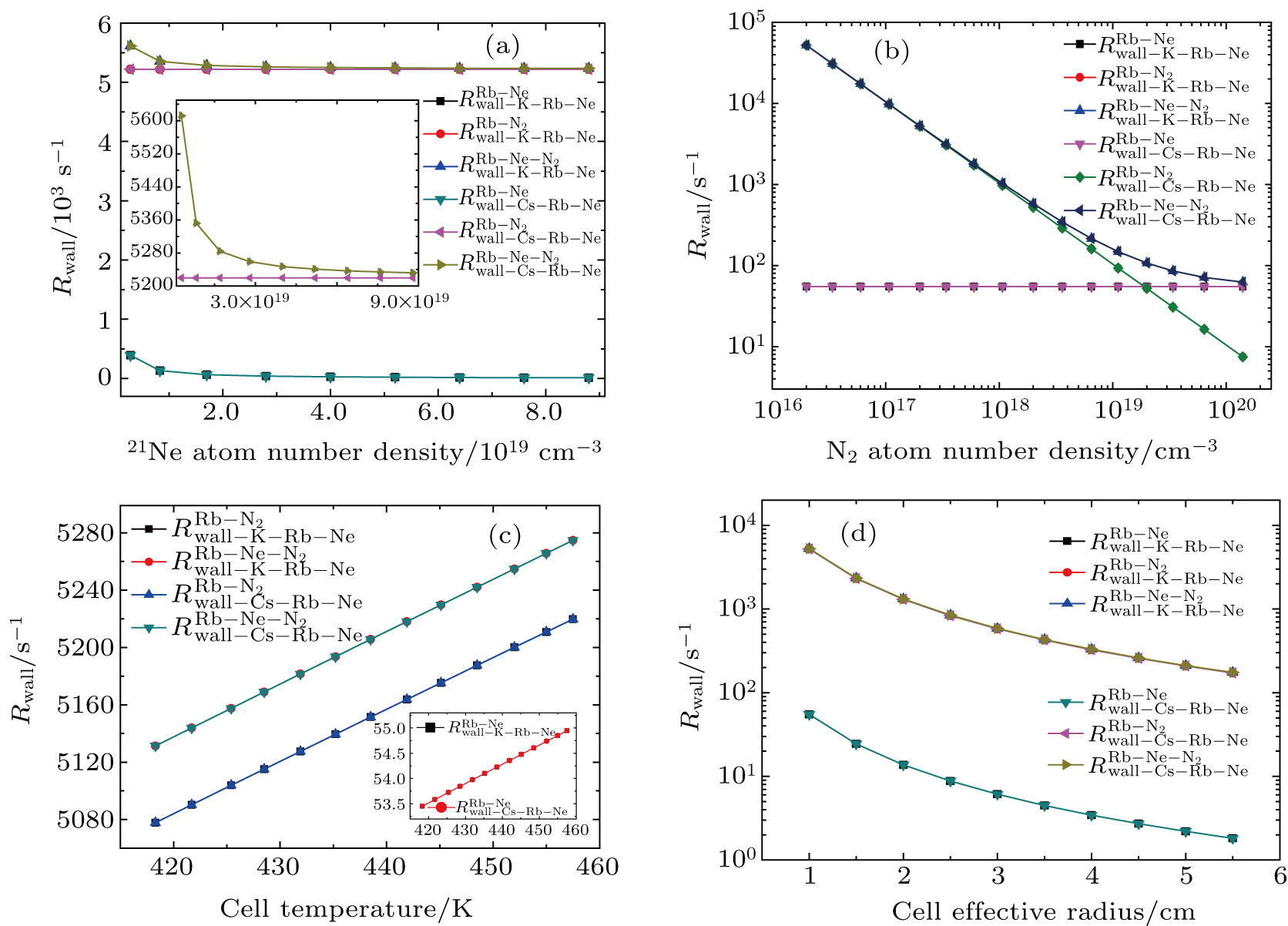 | Fig. 1. The wall relaxation rates change with the 21Ne number density nNe in (a), the N2 number density nN2 in (b), the cell temperature T in (c), and the cell effective radius a in (d). |
The 



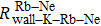

The polarization in the z direction could be calculated by[35]

The angle between the spins polarization and the z direction is small by applying a small magnetic field By, and the polarizations of K, Rb and 21Ne are approximately constant in the z direction, then the coupled Bloch equations can be simplified.[35] In the x direction, the polarizations of K and Rb can be solved and are given by[35]




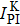

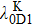
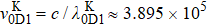

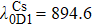


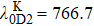
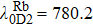

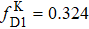




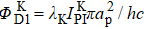


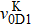
For small atomic polarization, the spin precession rate is given by ω0 = gμBB/Q(Pe)ħ, which is the Larmor frequency, TSE is the spin-exchange time, 
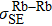
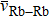





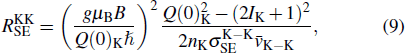
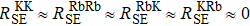
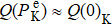
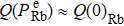
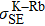
| Table 1. Parameters used for the calculation. . |
To improve the practicability of the HOPSERF co-magnetometers, it is necessary for us to investigate the fundamental sensitivity of the co-magnetometers to improve the sensitivity, stability of the co-magnetometers and to realize the miniaturization of the co-magnetometers. The fundamental shot-noise-limited sensitivity of an atomic gyroscope based on the co-magnetometer is given by[17,59]

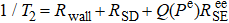
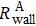
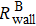
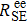
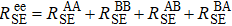
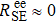







In the limit of fast spin-exchange and small magnetic field, the spin-exchange relaxation rate vanishes for sufficiently small magnetic field.[36] In Eq. (

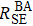

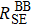

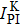

Because the slow-down factors are different in the polarization of 39K–85Rb–21Ne and 133Cs–85Rb–21Ne co-magnetometers, we take the slow-down factors at a low polarization limit for convenience of the theoretical analysis. The number density of the 21Ne, the power density of pump beam and the pump beam wavelength will affect the polarization greatly by affecting the pumping rate of pump beam. We systematically studied the variations of the pumping rate of the pump beam, frequency shift, Bn, Be, the relaxation rate for the alkali-alkali spin-exchange collisions. We obtain the following results by MATLAB and take several points to plot with Origin 8.
We choose one of 21Ne number density nNe, N2 number density nN2, cell temperature T, wavelength of pump beam λK(λCs), mole fraction of 85Rb fRb, cell effective radius a, and power density of pump beam 



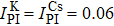
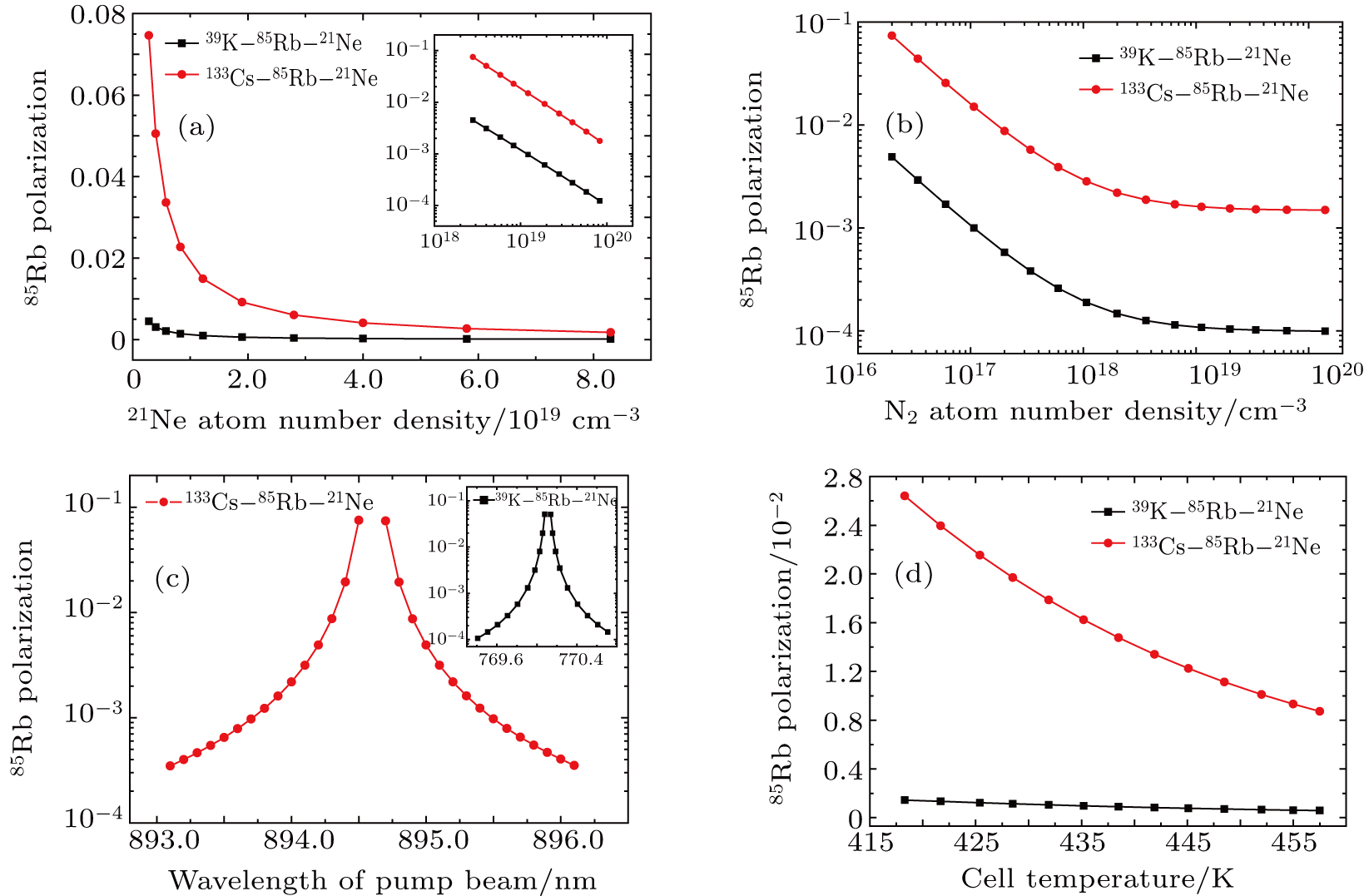
To ensure the validity of the low polarization limit and considering that the noble gas has enough magnetic moment which can compensate for the external magnetic field and the system can be a co-magnetometer, we make the 85Rb polarization smaller than about 0.08 and larger than 10–4. We discuss the variations of pumping rate of the pump beam, the frequency shift, the Bn, the Be, the alkali-alkali spin-exchange collision relaxation rate related with 85Rb atoms. Figure
Figure
From the formula of 







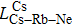

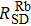
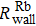
Figure 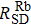

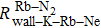

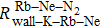
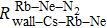




Figure 

Figure 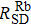



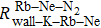
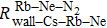











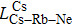
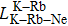


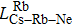
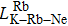









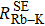







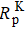







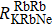

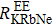

Figure
 | Fig. 3. The 85Rb polarization of 39K (133Cs)–85Rb–21Ne co-magnetometers versus the mole fraction of 85Rb (a), the cell effective radius (b), and the power density of pump beam (c). |
Figure 
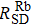


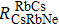


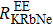

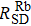
Figure 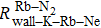




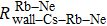
Figure 



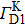






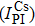
Figures 
We take 39K (133Cs) as the A atom, 85Rb as the B atom, one of the fRb, nNe, nN2, T, λK (λCs), 


Figure 
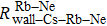



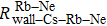
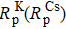
Figure 


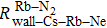
Figure
Figure 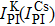
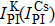

Figure 

The fundamental sensitivity of 39K (133Cs)–85Rb–21Ne co-magnetometers increase with the increasing cell effective radius a, respectively in Fig. 
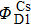
Figure
As a result, the polarization of the 85Rb atom of the co-magnetometer based on 133Cs–85Rb–21Ne is larger than the one based on 39K–85Rb–21Ne in Figs.
We obtain a fundamental sensitivity of about 7.542 × 10–11 rad·s–1·Hz–1/2 with 39K–85Rb–21Ne co-magnetometer with 85Rb polarization is about 4.4892 × 10–5 and nK/nRb ≈ 5.1228 × 10–4, a fundamental sensitivity of about 7.5355 × 10–11 rad·s–1·Hz–1/2 with 133Cs–85Rb–21Ne co-magnetometer with 85Rb polarization is about 8.193 × 10–4 and nCs/nRb ≈ 0.0043 when nNe = 6 × 1019 cm–3, nN2 = 6.3 × 1018 cm–3, T = 406.696 K, fRb = 0.99, 

We find that the 85Rb polarization of 133Cs–85Rb–21Ne co-magnetometer is larger than the one of 39K–85Rb–21Ne co-magnetometer in our chosen conditions. The fundamental sensitivity of 133Cs–85Rb–21Ne co-magnetometer is higher than the one of 39K–85Rb–21Ne co-magnetometer when (1) the external magnetic field is smaller than about 1.7884 × 10–8 T, (2) the mole fraction of 85Rb is larger than about 0.9662, or (3) the power density of pump beam is smaller than about 0.229 W/cm2.
To obtain a higher fundamental sensitivity between 39K–85Rb–21Ne and 133Cs–85Rb–21Ne co-magnetometers, we should choose 133Cs–85Rb–21Ne co-magnetometer [when (1) the external magnetic field is smaller than about 1.7884 × 10–8 T, (2) the mole fraction of 85Rb is larger than about 0.9662, or (3) the power density of pump beam is smaller than about 0.229 W/cm2] with 21Ne atoms as the buffer gas, take the critical values of 21Ne number density and quench gas N2 number density, increase the cell effective radius, the measurement volume, the cell temperature (when the quantity of alkali metal atoms are enough) and mole fraction of 85Rb atoms, reduce the external magnetic field and power density of pump beam, choose suitable wavelength of pump beam based on actual demand of the fundamental sensitivity and spatial resolution. We estimate the fundamental sensitivity limit of the co-magnetometers due to the shot noise superior to 7.5355 × 10–11 rad·s–1·Hz–1/2 with 133Cs–85Rb–21Ne co-magnetometer, which is higher than the one of a K–21Ne atomic co-magnetometer of 2 × 10–10 rad·s–1·Hz–1/2. We could choose suitable conditions on the basis of the experiment requirements to gain a higher sensitivity of the co-magnetometers, keep the costs down and carry forward the miniaturization and practical application of the co-magnetometers.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] |