† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11274149 and 11304185) and the Program of Shenyang Key Laboratory of Optoelectronic Materials and Technology, China (Grant No. F12-254-1-00).
Bauer recently presented a formula for the ionization rate of a hydrogen atom in a strong linearly polarized laser field [J. Phys. B
Keldysh–Faisal–Reiss (KFR) theory[1–3] describes non-resonant multiphoton processes such as the above-threshold detachment of ions and the above-threshold ionization of atoms in an intense electromagnetic (laser) field. The theory has provided fruitful insights into a wide range of highly nonperturbative processes in intense laser–atom physics. The two commonly used versions of KFR theory describe the same physical problem, and the main difference between them is the form of the laser–atom interaction in which the
KFR theory utilizes S-matrix theory, which is exact in principle. However, since there is no general analytical solution to the Schrödinger equation for a charged particle interacting with both the field of an attractive Coulomb center and the field of an electromagnetic plane-wave, we used analytical approximations to evaluate the S-matrix element for bound-free transitions. Therefore, various approximate theories could lead to different expressions of the ionization rate. The main approximations of the three versions of KFR theory are the single-active-electron (SAE) approximation,[8–10] electric dipole approximation (EDA),[11,12] and a version that neglects the interaction of the escaping electron with the long-range Coulomb potential[1–7] in the case of a neutral atom ionization. In addition to the above approximations, Keldysh applied two simplifications to the derivation of the ionization rate: (i) the saddle-point method (SPM) of approximation to perform the contour integral, and (ii) the small kinetic momentum assumption. Reiss did not face the above two limitations, and his formula for the ionization rate was expressed by generalized Bessel functions (GBFs). The description of any dynamic process in atomic physics should be gauge-invariant,[13–15] meaning that calculations by two models must yield the same results. However, apparent discrepancies have been observed between the predictions from strong field approximations in the velocity and length gauges. As is well known, the two models can yield very different and occasionally contradictory results in strong electromagnetic fields.[16–23] Recently, Bauer[24] proposed a formula for the ionization rate of a hydrogen atom in a strong linearly polarized laser field. It began from the LG, but used a GBF analytical method. The numerical results calculated with his formula were compared with the results from other models. However, it remains unclear what will happen if we derive a formula by starting from S-matrix theory in velocity gauges and using the analytical SPM at the same time. In this paper, we intend to answer this question.
This remainder of this paper is organized as follows. In Section
In this section, we derive a formula for the ionization rate of an atom. We use the VG and SPM to perform the contour integral, in the way that Keldysh used the LG. Then, we present a formula for the energy spectrum of a photoelectron. There ae two conditions necessary for deriving the final expressions of the ionization rate as noted by Keldysh[1,4,5] and others.[24] The first is adiabatic approximation, which is necessary to perform the integral with the SPM. The second is the small final kinetic momentum approximation.
Considering hydrogen atoms in the bound state in a linearly polarized laser field, the S-matrix element describing the probability of direct transition from a bound state to a free state can be expressed as
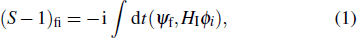
The Hamiltonian interaction between the laser field and the outgoing electron in the VG can be written as
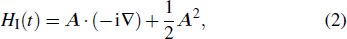
According to the strong field approximation, the influence of the interaction of the remaining atom in the final state with the escaping electron is entirely neglected. This approximation is supposed to be valid for a very intense field, when the oscillation energy of the detached electron in the laser field dominates the atomic binding energy. The Volkov state can be written as
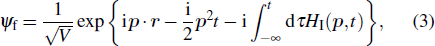

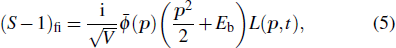
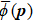
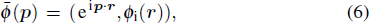


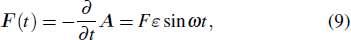
An integration can now be carried out over τ in Eq. (
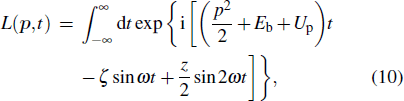
Using GBFs,
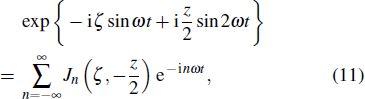
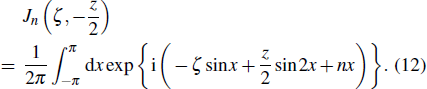
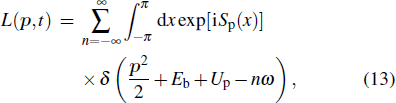
The saddle point integral method is used to integrate over x = ω t, and the position of the saddle point is determined by dSp/dx = 0. Equations (
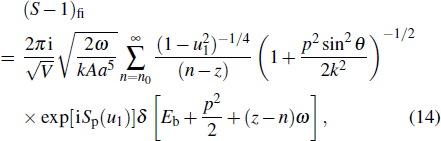
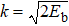
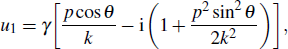
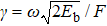
According to the method of Lin et al.,[25] pre-exponent factors can be represented approximatively in the exponent forms. Equation (



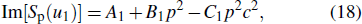

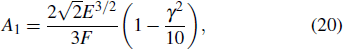




The differential ionization rate w can be found from
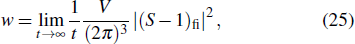
The total photoionization rate can be derived from the integral of w as follows:
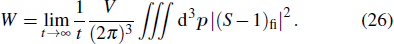
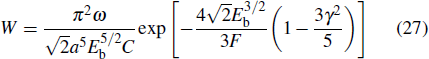
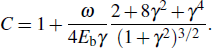
The energy distribution of photoelectrons can be written as

In this section, we present the numerical results calculated with our formula, and compare them with the results from the formulae given by Keldysh, Reiss, and Bauer,[1,2,24] which are obtained by using different combinations of gauges (LG or VG) and analytical methods (SPM or GBF). The formula derived by Keldysh[1,4,5,24] utilizes the LG and the analytical SPM is expressed as
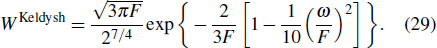
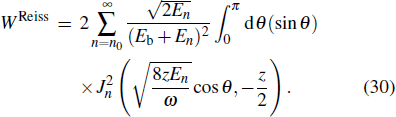
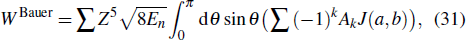
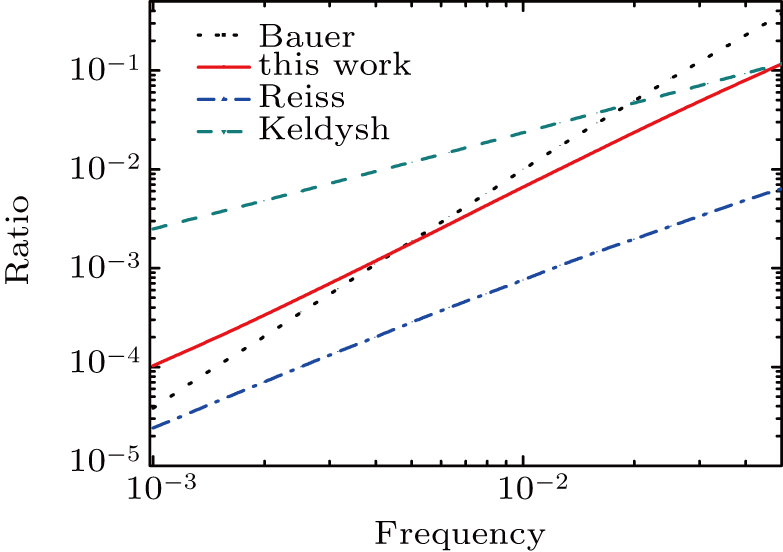
In order to reveal the apparent discrepancies among the results of the four formulae, we calculate and compare the ratios of the ionization rates by using different formulae and the static field ionization rate 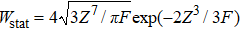
First, we fix the frequency ω = 0.01 a.u. and the ionization rate as a function of the Reiss intensity parameter z1. The results are shown in Fig.
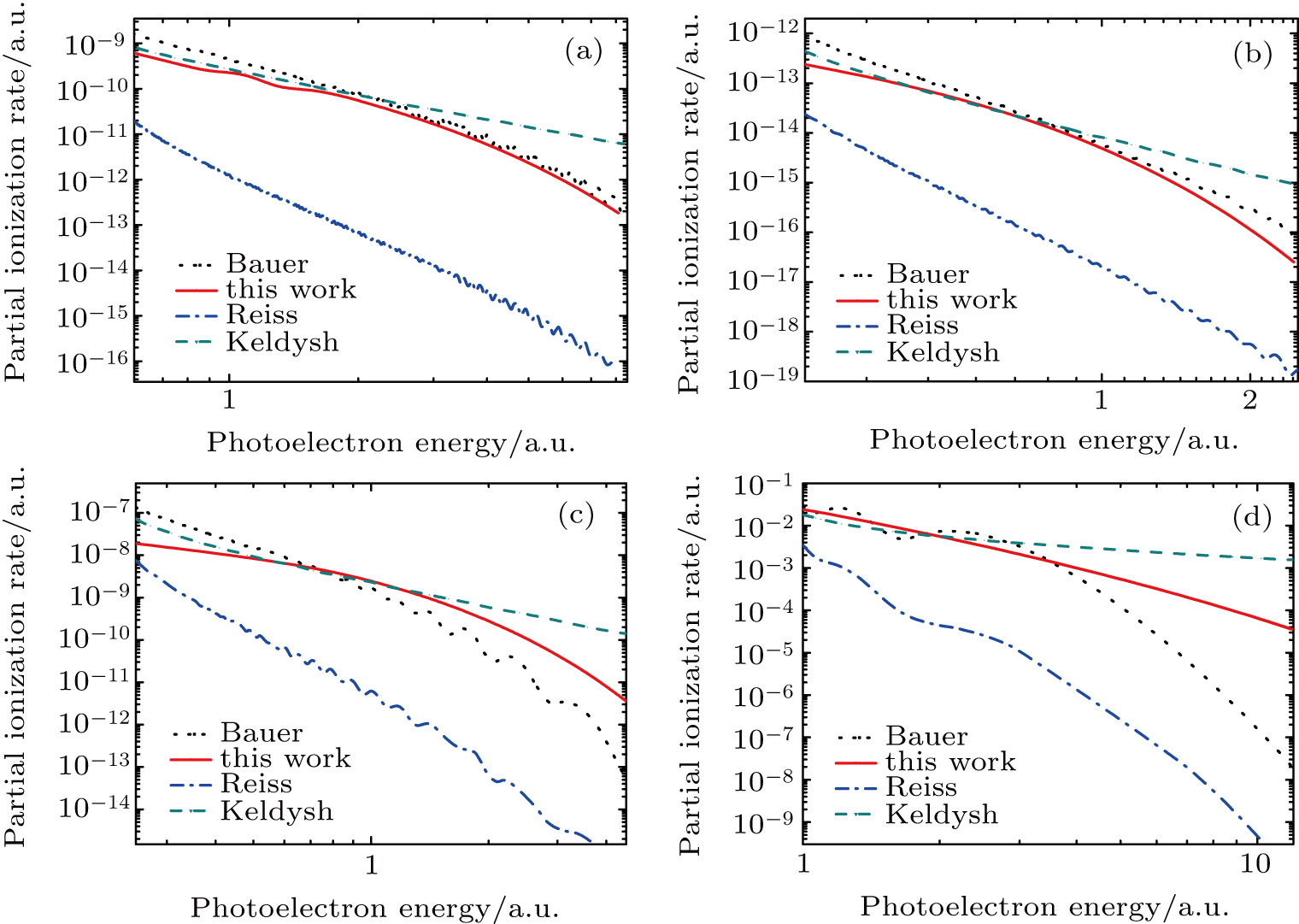
Next, we calculate and compare the photoelectron energy distributions of the different models. The results are shown in Fig.
We derived the formula for the ionization rate and photoelectron energy distribution of a ground-state hydrogen atom exposed in a linearly polarized laser field by using the VG and the analytical SPM. In our numeric calculations, the laser parameters are limited in the tunnel region ω ≪ 1 and z1 ≫ 1 to satisfy the applicable condition of our formula and that of Keldysh, and the final kinetic momentum is small. The comparisons of our calculated results with the original results obtained by the Bauer, Keldysh, and Reiss theories show that our derived formula is simple and easy to understand, and that the calculated results are closer to the results of Keldysh. More importantly, our results reduce the discrepancies between the LG and the VG. This study fills a gap in the literature regarding the combination of gauges with analytical method in KFR-like theory. Discrepancies in the ionization rate are caused not only by the different gauges, but also by the different analytical methods used to derive the ionization rate. We expect that our study will help to further study the ionization mechanism of hydrogen-like atoms.