Controlling microscopic electron process lies in the core of study on intense light interacting with various matters.^[1] When atoms or molecules are irradiated by intense laser fields, bound electrons can be ionized. The freed electron may turn back to its parent core when the electric field of the laser light reverses, which triggers many subsequent processes, such as rescattering process^[2] and harmonic generation,^[3–5] etc. The rescattered electron interferes with the directly ionized electron, changing the photoelectron angular distributions (PADs)^[6] and causing the spider-lag structure in the PADs.^[7] When the freed electron recombines with its parent core, high order harmonics are emitted in the attosecond time scale, which is an important source of attosecond pulse. Controlling the interference structure in the PADs and generating the attosecond pulses by modulating the driving laser fields were widely studied in the past decades.^[8,9]

Non-sequential double ionization (NSDI) is also an important phenomenon frequently studied in the laser–atom interaction.^[10–12] According to a three-step scenario,^[13] the NSDI phenomenon denotes a process in which the returned electron collides with the parent nucleus. The impact increases the ionization rate of the second electron, and sets up an electron correlation. The electron collision and the electron correlation in the NSDI process were frequently studied.^[10,14,15]

The electron correlation is established when the freed electron goes back to the vicinity of the parent core.^[12,16–18] In a linearly polarized laser field, the freed electron encounters the nucleus twice in one optical cycle. Therefore, in a long laser pulse, the electron collision may occur in different moments. Consequently, the electron correlation is averaged among these multiple collisions and the essential features of a single collision are lost.^[14] To disclose the losing features of the electron correlation, it is necessary to limit the electron collision occurring only once and at a time interval as short as possible. To this end, one may choose ultrashort laser pulses, but has to suffer the extremely low NSDI rate. Another choice is to increase the peak intensity, but the ionization will occur in the leading edge of the laser pulse. Thus one has to use the deliberately modulated laser pulses.^[15] How to get single electron collision in a laser pulse is still an open problem.

Recently, the NSDI in counterrotating circular two-color (CRTC) fields have aroused much attention.^[19–23] Both experimental and theoretical studies have shown that the CRTC fields can significantly improve the NSDI rate.^[24] Meanwhile, the CRTC fields provide more parameters that can be used to control the electron collision. Chaloupka et al. have shown that the electron collision is finished within 0.2 optical cycle after the first electron is ionized.^[20] This suggests the ionized electron travelling a very short trajectory before colliding with the parent core. This paves a way to control the electron collision by using the CRTC field. However, the laser conditions used to get the single collision in Ref. [20] are only suitable for He target, so more general conditions suitable for other targets still need to be explored.

In this paper, we study the NSDI of Ar atoms in the CRTC laser field and we focus on how to control the electron collision by choosing the proper laser fields. In order to obtain a single electron collision, we use a scaling technique to determine the driving laser field parameters. We will show that the electron collision process varies with frequency, peak intensity, and field ratio of the CRTC field, and can be limited to a sub-femtosecond time scale by properly choosing these parameters. The optimal conditions to control the electron collision are also discussed.

The method used here is based on the numerical integration of the time-dependent Newtonian equation, which is very effective in dealing with the NSDI phenomena.^[25–27] Details of the method are presented in Ref. [28]. In brief, the motion of two electrons is governed by the canonical equation as

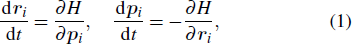
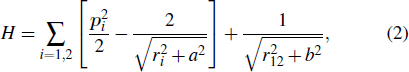
The energy of two electrons in the CRTC field varies with time. When the energy of an electron becomes positive, the electron is treated as being ionized, and the moment is regarded as the time of ionization. A double ionization (DI) event is counted if both electrons are ionized at the end of the laser pulse, and the moment of the second ionization is denoted as the time of DI. The time of electron collision is counted as the moment when the two electrons reach their shortest distance after first ionization. The back-trajectory technique^[25,27] is used to seek for these moments.

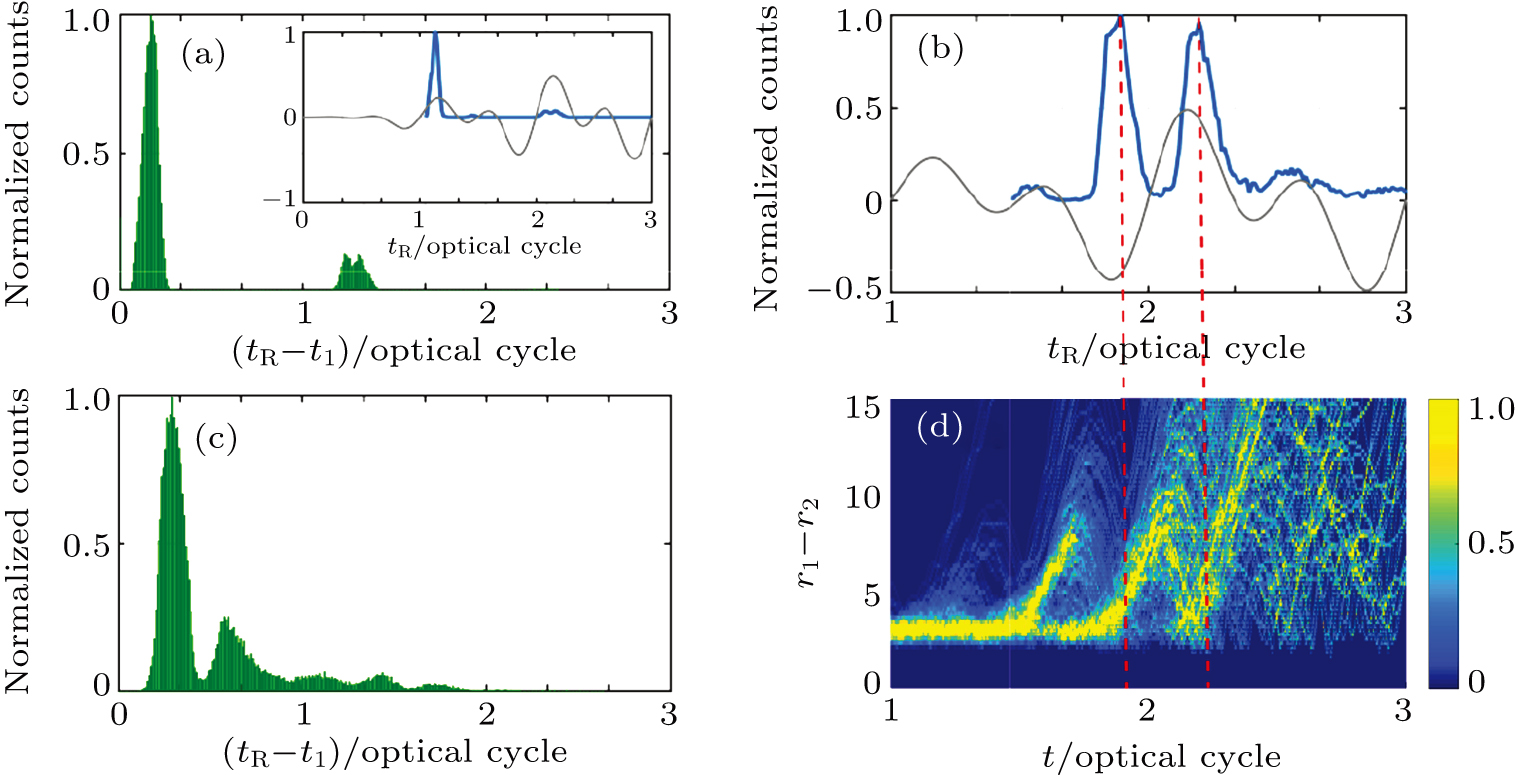
The Ar atoms are frequently used target in the NSDI study, we mainly study the NSDI process of the Ar atoms. In the CRTC driving fields, the electron collision generally occurs in multiple time intervals,^[22] so it is still not easy to get a single electron collision. Recently, using the CRTC field, Chaloupka et al. found that the electron collision in the NSDI of He target can be finished within 0.2T after the first electron is ionized.^[20] This suggests the electron collision can be accurately controlled by using the CRTC fields. For the convenience of comparison and for a deep insight to the electronic dynamics, we first study the electron collision in the He atoms and then focus on the NSDI process of Ar atoms.

Figure 1(a) shows the number of the electron collision events varying with the time difference between the first ionization (denoted by t₁ ) and the electron collision (denoted by t_R ) for the He atoms driving by the CRTC field. Similar to that shown in Ref. [20], a single sharp peak appear in the variation curve, which implies that the electron collision occurs concentratedly after the first ionization. To confirm the electron collision moment, we depict the variation varying with t_R in the insert. The curve shows similar structure but starts from the second optical cycle. This indicates that both the first ionization and the electron collision are archived very convergent in time.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Panels (a)–(c) show the variation of electron collision events with tR–t1 and tR, respectively. Panel (a) is for He atoms driven by 1016-W/cm2 field, and the insert shown the variation with tR. Panels (b) and (c) are for Ar atoms driven by 2.0 × 1014-W/cm2 field. Each curve is normalized by its maximum, and t1 and tR denote the time of the first ionization and the electron collision, respectively. Panel (d) shows the time variation of the two-electron distance distribution. Vertical red dot line indicates the correspondence between the electron collision peaks and the two-electron distances. The driving field is the 800 nm–400 nm CRTC field, and the optical cycle denotes the period of 800-nm field. The x component of the electric field is also marked by the light gray lines in panels (a) and (b).

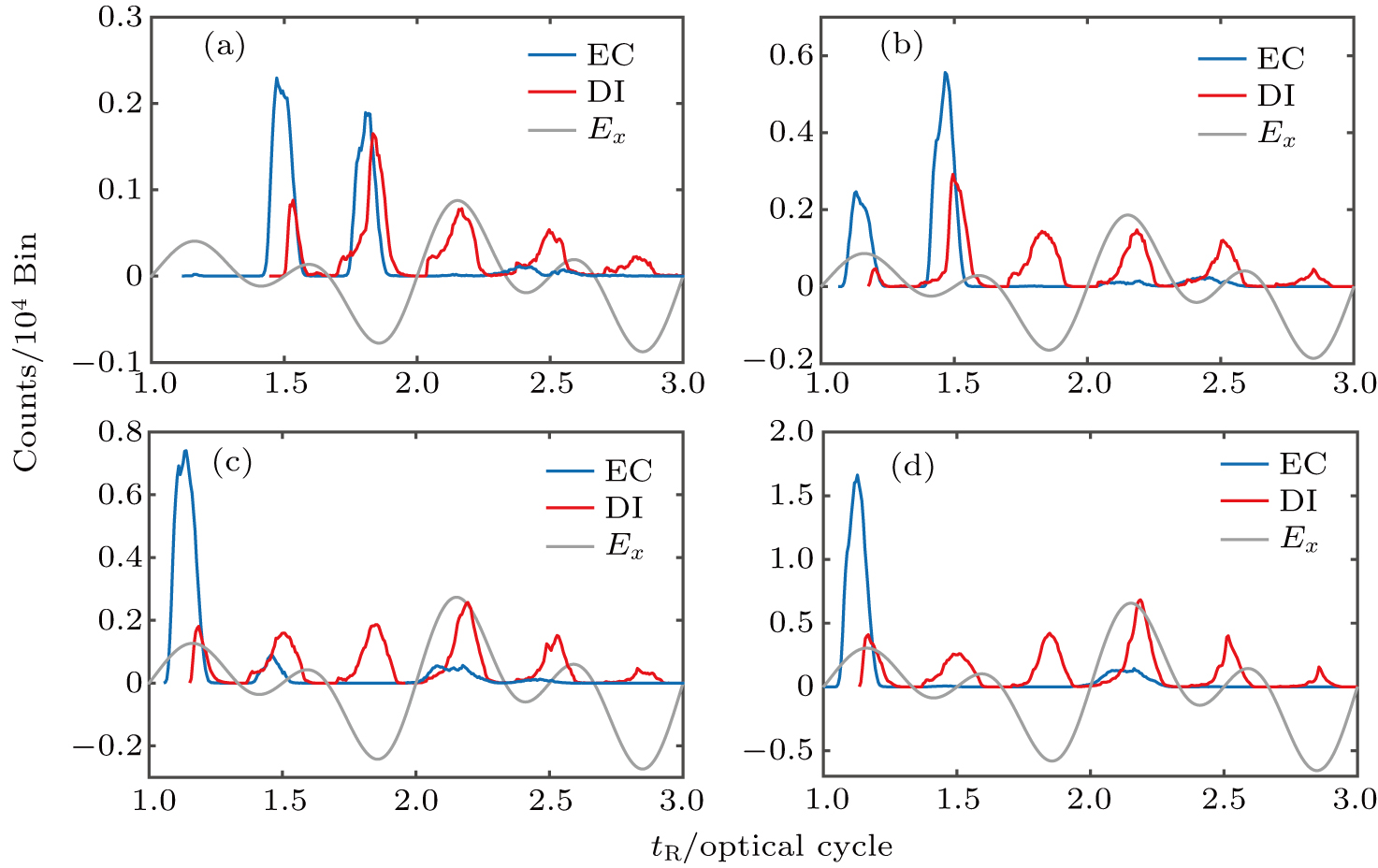
Next we study the NSDI of Ar atoms in the CRTC field of 800-nm wavelength but of lower intensity. Figures 1(b) and 1(c) show the number of the electron collision events varying with t_R and t_R–t₁, respectively. The t_R–t₁ curve for Ar atoms, which are quite similar to those of He atoms, where a sharp peak located at the beginning of the time axis dominates the curve. However, this does not mean that the electron collision occurs in a short time, because the t_R curve shown in Fig. 1(b) exhibits two notable peaks. These two peaks are of comparable weights, indicating that the electron collision occurs mainly in two neighboring leaves of the electric field.

To get a further insight into the electronic dynamics in the CRTC field, in Fig. 1(d) we depict the variation of the two-electron distance with time. The correspondence with the t_R curve clearly shows the first ionization and the electron collision process. Before ionization occurs, the two electrons move around the core, and thus their distance is short in general. The first ionization occurs mainly at the two time intervals. One starts from 1.6T and finishes at about 1.8T, and the distance of the two electrons increases distinctively during this time interval. The ionized electron travels a short trajectory and then returns, followed by the collision with the remaining electrons which occurs mainly around 1.85T. The collision triggers the second ionization which leads to the distance of the two electrons increasing fast again. Meanwhile, this fast increase in the two-electron distance is contributed mostly by the first ionization. Similar to that occurs in the first time interval, the electron ionized at the second time interval also travels a short trajectory and then goes back to the core. The colliding of the first electron with the remaining electrons triggers the second ionization at about 2.2T. From then on, the two-electron distance increases again. In general, both the first ionization and the electron collision occur mainly at two time intervals, but the time delay between these two processes keeps very short.

From the above discussion we see two points of NSDI process in the CRTC fields. One is that for the same field ratio, the t_R–t₁ curves keep similar features and the electron collision occurs shortly after the first ionization, which implies that the first ionized electron travels a very short trajectory in the CRTC field. The other is that the moment of electron collision may be quite different, although the time difference t_R–t₁ is quite small. This suggests that the t_R curve discloses more details of the electron dynamics in the CRTC field. In the following, we mainly study the variation of t_R curve with the laser fields.

In addition to the laser fields, the binding energy of the targets also affects the electronic dynamics. Under similar laser conditions, the electron collision occurred in the He target may differ greatly from that happens in the Ar target. In order to obtain the field parameters which are suitable to control the electron collision in other atoms, we use the scaling technique.

The scaling law for photoionization in intense laser fields was firstly proposed by Guo et al.^[29] and was extended to the NSDI process recently.^[30,31] The scaling law shows that electronic dynamics for atoms driven by a laser light of the frequency ω and intensity I is the same for another kind of atoms driven by a laser light of frequency kω and intensity k³ω, where k is the scaling parameter and equals the ratio of the second ionization potentials of two atoms. The electron correlation in different targets can be equivalent if one chooses the laser field according to the scaling law^[32] and the conditions to observe the knee structure in rare atoms was found.^[33] This suggests a way to get equivalent electron collision process in the target other than He atoms provided that he chooses the driving field according to the scaling law.

According to the scaling law, we choose ω = 0.028 a.u. (1575 nm) fields to drive the Ar target, which equals 0.508 times to that drives the He target. In Fig. 2 we exhibit the time variation of both the electron collision (EC) and the DI counts for several combined intensities. The two colors are of equal intensity. Generally, the EC curves show several sharp peaks, denoting that the electron collision occurs in many time intervals but each electron collision is very convergent in time. The height and location of two peaks vary with the laser intensity, indicating the change of the collision probability and the occurrence time of the electron collision with the laser intensity. As the laser intensity increases, the moment of the first ionization as well as the subsequent electron collision moves forward gradually. Owing to the ionization saturation effect, the time window of the first ionization also becomes narrow. When the laser intensity is high enough, the first electron is ionized during one half cycle in the leading edge of the pulse, which leads to the electron collision also being finished in one half cycle. The higher the laser intensity is, the earlier the collision occurs. For 3.0 × 10¹⁴ W/cm², see Fig. 2(a), two sharp peaks are of comparable heights and dominate the EC curve, indicating that the electron collision occurs mainly in these two time intervals. For 6.0 × 10¹⁴ W/cm², see Fig. 2(b), the second peak is the highest one and locates at around 1.5T, indicating that more than half EC events occur at this moment. When the laser intensity is increased to 9.0 × 10¹⁴ W/cm², the EC curve shows a single prominent peak, and the EC events occur mainly in this short time interval. This phenomenon is more evident when the laser intensity is further increased. When the laser intensity reaches 1.34 × 10¹⁵ W/cm², a pure single peak becomes the only notable structure in the EC curve. All of the EC events occur in a time interval as short as 0.2T, which implies that the electron collision is confined into a sub-femtosecond time scale. This case is similar to that in the He target, and the laser intensity agrees well with that obtained by the scaling law. On the contrary, the DI curves exhibit many peaks, most being a little broad than the collision peak. From these figures, it is easy to identify the double ionization process. The leading one or two red peaks follow the blue peaks very closely, which indicates that the second electron is ionized shortly after electron collision. This is for the recollision-induced ionization (RII) process. The rest red peaks lag behind the blue peaks more than half an optical cycle at least, indicating that the second electron is ionized by the recollision-induced excitation followed by sbusequent-field ionization (RESI) process. With the increase of laser intensity, the peaks in DI curve become more flat, denoting that the RESI process takes place in larger time intervals. In brief, the electron collision can be achieved in a very short time interval by changing the intensity of the combined laser field.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Variation of the EC and the DI counts with time. The ω–2ω CRTC fields are of intensity (a) 3.0 × 1014 W/cm2, (b) 6.0 × 1014 W/cm2, (c) 9.0 × 1014 W/cm2, and (d) 13.4 × 1014 W/cm2, respectively. The laser wavelength is 1575 nm and the two colors are of equal intensity. The x component of the electric field is marked by light gray lines.

In the CRTC field, the field ratio of two colors, say ε in Eq. (3), is an important parameter. It has been shown that both the traveling time of the first electron and the ionization time delay of two electrons change greatly with the field ratio of two colors.^[34] In order to explore the influence of field ratio on the electron collision and get an optimal control, we calculate the EC time and the DI time for other field ratios, and some results are shown in Fig. 3 for a combined laser intensity 9.0 × 10¹⁴ W/cm². Figure 3(a) shows the time variation of the EC and the DI counts for ε = 0.8. The electron collision occurs in a very short time interval and the EC curve exhibits mainly a single sharp peak. The second ionization occurs at each time when the electric field reaches to its maximum, so the DI curve exhibits several broad peaks. When the field ratio changes, all curves vary a lot. As shown in Fig. 3(b) for ε = 1.5, the first peak in the EC curve becomes broad and additional peaks get notable, and the peaks in the DI curve become float. This trend is even more clear for larger field ratio, as shown in Fig. 3(c) for ε = 2.0. We then conclude that a better choice to control the electron collision is to set ε = 1.0±0.2 for the laser intensity higher than 9.0 × 10¹⁴ W/cm².

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Variation of EC and DI counts with time. The intensity of the ω–2ω CRTC field is 9.0 × 1014 W/cm2 and the field ratio is (a) 0.8; (b) 1.5; and (c) 2.0. Other parameters are the same as those in Fig. 2.

The pulse duration is an important factor affecting the double ionization process, especially when the laser intensity is not so high that the RESI process dominates the NSDI process. However, as the laser intensity is so high that a single collision is achieved, the double ionization occurs mainly in the leading edge of the pulse, and thus further increasing the pulse duration will not lead more double ionization greatly and our conclusion holds for laser pulses longer than five-cycle duration.

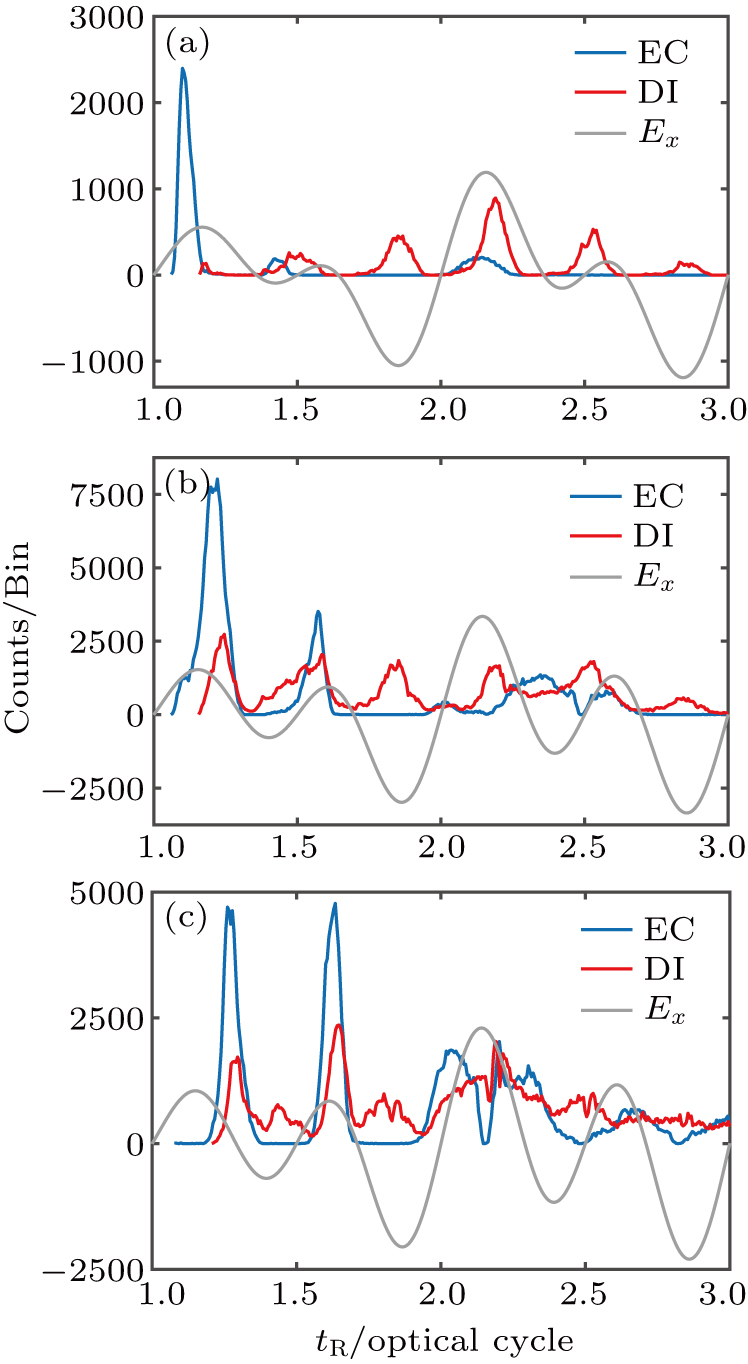
The ω–3ω CRTC field is another frequently used field in the study of NSDI. Compared with the ω–2ω CRTC field, where the combined electric field forms a clover-leaf structure, the electric field of the ω–3ω CRTC field exhibits a four-leaf pattern. This suggests the electric field in the ω–3ω CRTC field varies more quickly and the electron collision is expected to be finished in less time than that in the ω–2ω CRTC field. For this purpose, we study the electron collision in the ω–3ω CRTC fields, and some EC and DI curves are shown in Fig. 4. From this figure we see that the two curves exhibit peaks and each peak becomes more sharp. In Fig. 4(a), for 3.0 × 10¹⁴ W/cm², three main peaks in the EC curve are notable. As the laser intensity increases, these peaks shift forward gradually and the third one becomes weak. This is because the electric field reaching the ionization threshold earlier in higher intensity fields. When the laser intensity is increased to 1.34 × 10¹⁵ W/cm², as shown in Fig. 4(d), only one peak is notable in the EC curve. This means a single electron collision is achieved in a convergent time. Each peak becomes more sharp and narrow in the ω–3ω CRTC fields. The electron collision can be finished within a time interval as short as 0.1T. The DI curve shows four peaks in one period. This is because the electric field reaching the maximum four times in one optical cycle, and electrons are easier to be ionized at the peaks of the electric field. Further research shows that both the EC curve and the DI curve change with the field ratio, but the best ratio to gain the shortest collision time is still around 1.0.

Fig. 4.

	Figure Option ViewDownloadNew Window
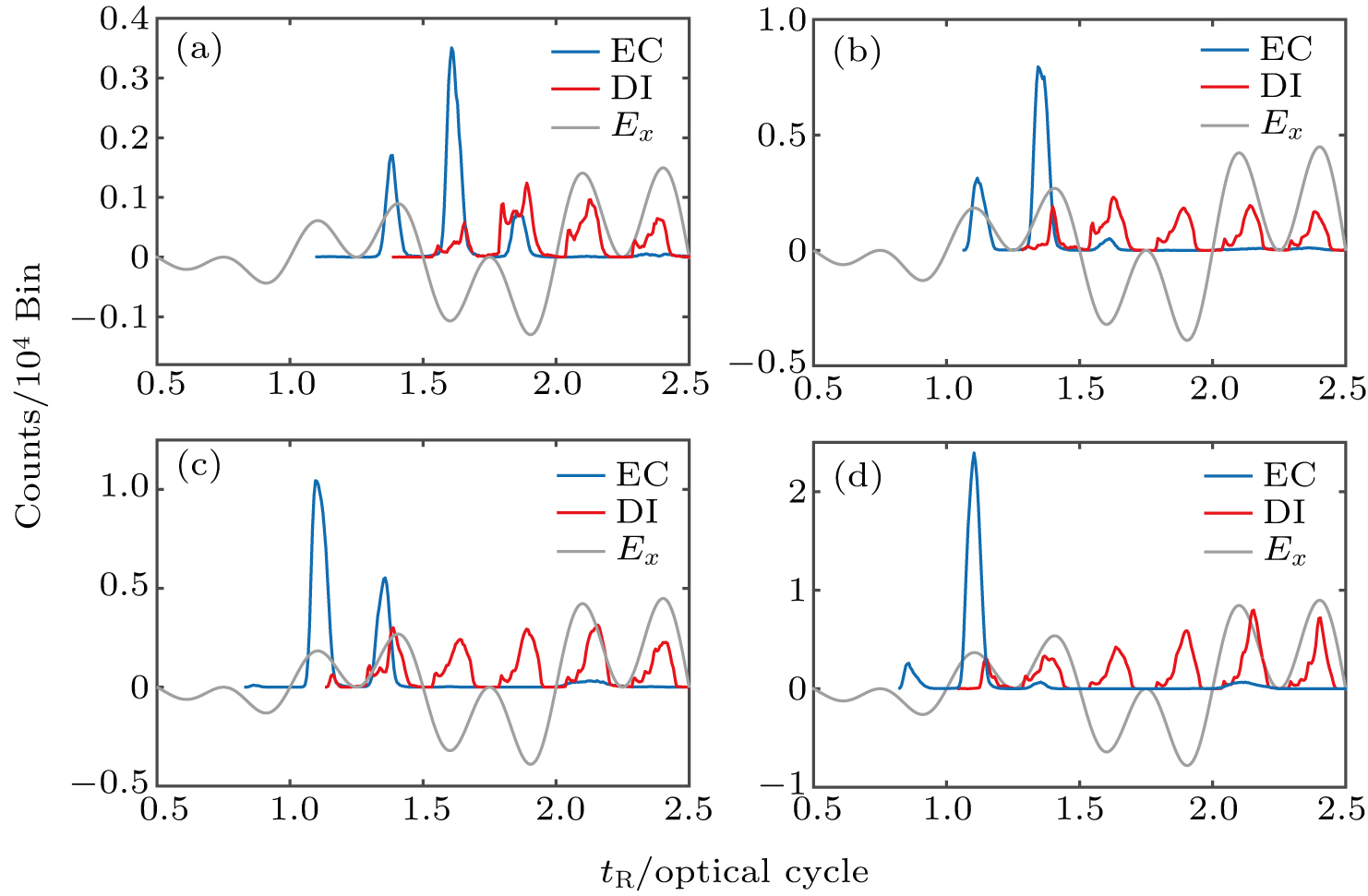	Fig. 4. Variation of EC and DI counts with time in ω–3ω CRTC fields. Other conditions are the same as those in Fig. 2.

In brief, we have shown that the electron collision can be achieved within 0.2T in the ω–2ω CRTC field, provided that the combined laser intensity is higher than 0.9 × 10¹⁵ W/cm² and the field ratio is about 1.0±0.2. Further study discloses that when the laser intensity is in a range of 0.9 × 10¹⁵ W/cm² to 1.7 × 10¹⁵ W/cm², the EC curve shows a single peak. For the ω–3ω CRTC field, the collision time can be further limited within 0.1T, when the laser intensity is in a range of 1.3 × 10¹⁵ W/cm² to 1.5 × 10¹⁵ W/cm². For one optical period is about 5.3 femtosecond, our finding suggests that the electron collision can be finished within sub-femtosecond time scale.

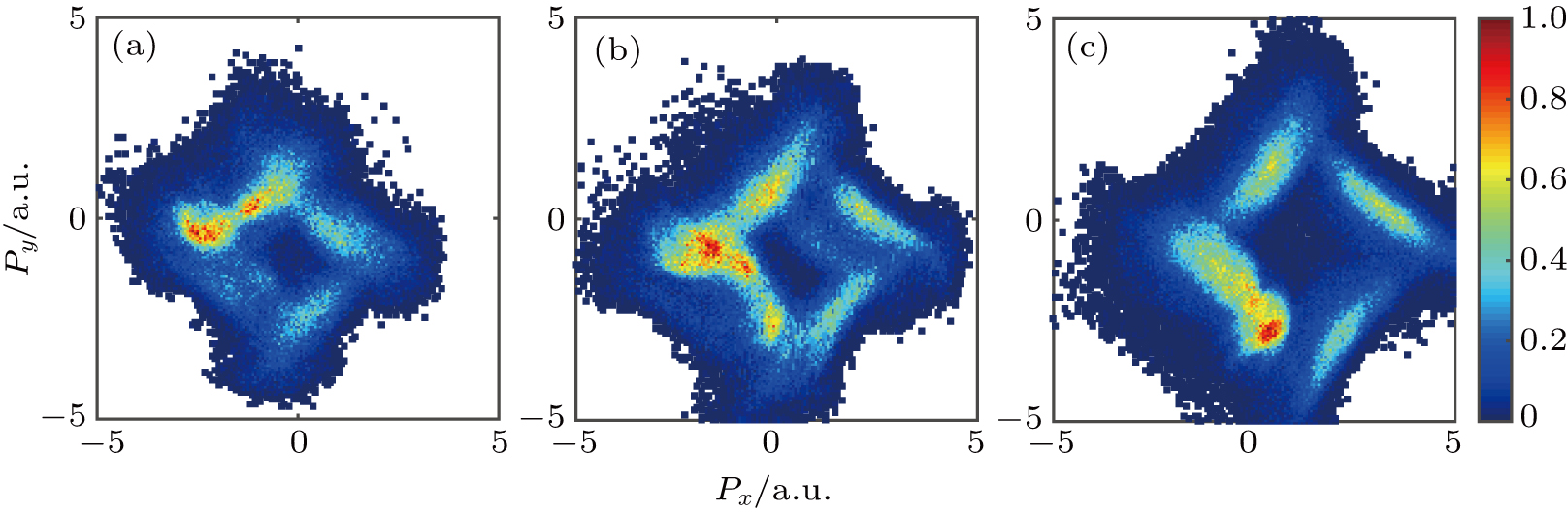
Momentum distribution (MD) is frequently studied in NSDI. It provides an important assist to disclose the electron collision features. A question is what will it be when a single electron collision occurs in such short time scale? To answer this question, we study the MDs of electron pairs released via the RII process. It has shown that the final momentum of the ejected electron includes the initial momentum shortly after collision and the drift momentum that equals the vector potential of the laser field at the moment that it was born. For the RII electrons, two electrons can be treated as being ionized at the same time, so the drift momenta are the same. Therefore, the MD of the RII electrons encodes the momentum distribution at the moment of the electron collision.

Figure 5 shows the MDs of the recoil ion in the RII process driven by the ω–2ω CRTC fields. Bright region is highlighted in the triangle blue background. The blue background discloses the shape of vector potential of the CRTC field, and the bright region accumulates the high probability EC events. At lower laser intensities, as shown in Fig. 5(a), the bright region is not so regular, denoting that the electron collision happens in a broad time interval. As the laser intensity increases, the bright region tends to be triangle type, and the reddish region becomes more notable, as shown in Fig. 5(b). The two reddish dots denote the two peaks in the EC curve. The two reddish pots merge into one for further higher laser intensities, as shown in Fig. 5(c). In this case, only one peak appears in the EC curve, denoting that most electron collisions occur only one time and in a short time interval.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. MDs of the recoil ion in the RII process driven by the ω–2ω CRTC fields. The two colors are of equal intensity and the combined intensity is (a) 3.0 × 1014 W/cm2, (b) 6.0 × 1014 W/cm2, and (c) 9.0 × 1014 W/cm2, respectively.

Figure 6 shows the MDs of the recoil ion in the RII process in the ω–3ω CRTC fields. Also, we find bright region highlighted from the blue background, which is similar to the ω–2ω case. The difference is that both the bright region and background become diamond type. This is caused by the change in the vector potential of the driving field. Two reddish pots appear in the bright region of Fig. 6(a), but in Fig. 6(b) only one big reddish pot becomes notable, indicating the electron collision time becomes convergent. When the laser intensity is increased to 1.34 × 10¹⁵ W/cm², the reddish pot is dominant in the bright region. In this case, most electron collisions occur only once and in a short time interval, similar to that in the ω–2ω case. The position of the reddish pot also varies with the laser intensity, denoting the optimal electron collision occurring in different time.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. MDs of the recoil ion in the RII process driven by the ω–3ω CRTC fields. The two colors are of equal intensity and the combined intensity is (a) 6.0 × 1014 W/cm2, (b) 9.0 × 1014 W/cm2, and (c) 13.4 × 1014 W/cm2, respectively.

The electron collision in the NSDI process of atoms can be controlled by properly choosing intensity and frequency of the CRTC driving fields. For the Ar atoms driven by the CRTC field with a fundamental wavelength of 1575 nm, the electron collision can occur only once within sub-femtosecond time scale. When the Ar atoms are driven by ω–2ω CRTC fields, the electron collision can occur within 0.2T. The optimal laser intensity is among the range of 0.9 × 10¹⁵ W/cm² to 1.7 × 10¹⁵ W/cm². When the Ar atoms are driven by ω–3ω CRTC fields, the electron collision can be limited within 0.1T. The optimal laser intensity is 1.3∼1.5 × 10¹⁵ W/cm². The optimal field ratio of the two colors is about 1.0. When the single electron collision occurs, the MD of the recoil ion in the RII process exhibits a single maximum, and a net electron correlation is set up. The proposed method is also valid for other atoms, provided that one chooses the frequency and intensity of the CRTC field according to a scaling law.