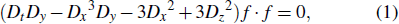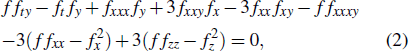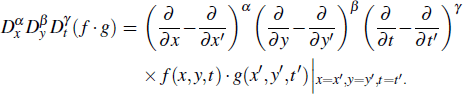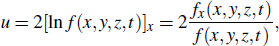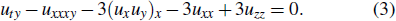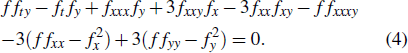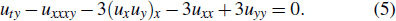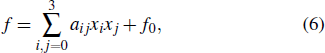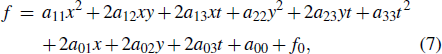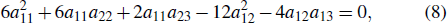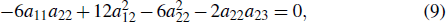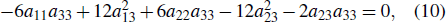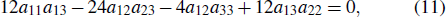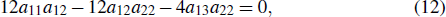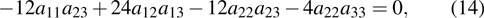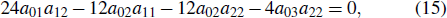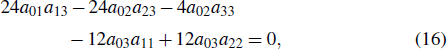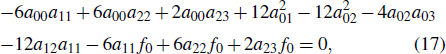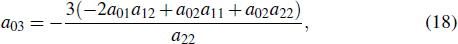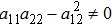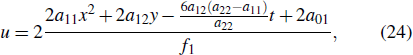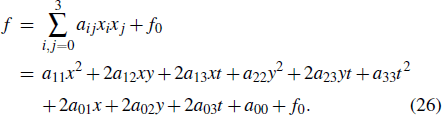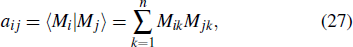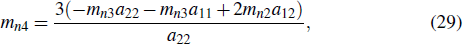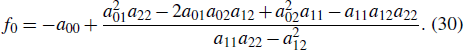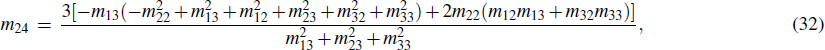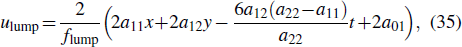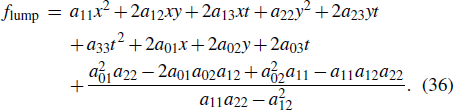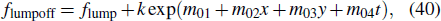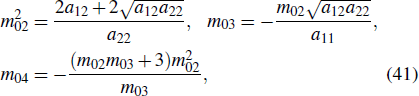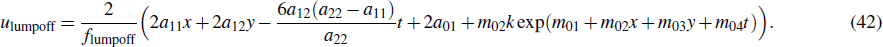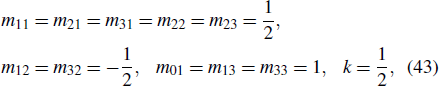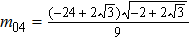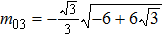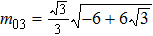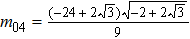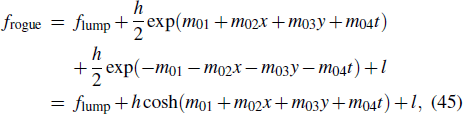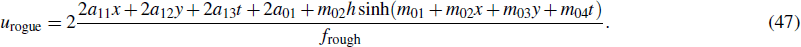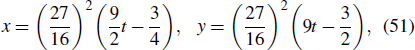Lump, lumpoff and predictable rogue wave solutions to a dimensionally reduced Hirota bilinear equation
School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China
† Corresponding author. E-mail:
zhangyfcumt@163.com
Project supported by the National Natural Science Foundation of China (Grant No. 11971475).
1. IntroductionIn recent years, the theme of lump waves in nonlinear science has attracted great interests because it was regarded as suitable prototypes to model rogue wave dynamics in both nonlinear optics[1] and oceanography.[2] In Ref. [3] the author proposed an effective method for constructing the lump solutions to the Kadomtsev–Petviashvili equation, and then all second-order lump solutions were systematically presented in Ref. [4] by Ma and Zhou. Henceforth, many nonlinear partial differential equations also admit lump solutions, such as the generalized Kadomtsev–Petviashvili–Boussinesq equation,[5] the Boussinesq–Kadomtsev–Petviashvili equation,[6] the (2+1)-dimensional Ito equation,[7] and the (2+1)-dimensional Burgers equation.[8] etc.[8–19] Many methods can help us study lump solutions, such as the multiple variable separation method[20] and the common expression method.[21] Among them the Hirota bilinear method is recognized as an effective approach to find lump solutions to nonlinear partial differential equations. The large amplitude wave related to the rogue wave is an extreme event that appears on the surface of the ocean. Such waves can be accompanied by deep grooves (holes) that appear before and/or after the maximum peak. Recently, special attention to theories and experiments has spread from oceanography into several other areas of research, such as nonlinear optical systems,[22,23] fluid dynamics and atmosphere.[24–31] These developments help to understand the physical mechanisms of the flow phenomenon.
Jia and Lou[32] gave one special case of the lump solutions to the (2+1)-dimensional KP equation based on the general mathematical results established in Refs. [3,4] After that, the lumpoff solution and the instantan/rogue wave solution were derived. Based on the completed study, a series of related work was carried out.[33–36] In this paper, we mainly consider a new (3+1)-dimensional model equation introduced by using a multivariate polynomial in Ref. [37] and then discuss the lump dynamics related to the new Hirota bilinear equation.[38] The form of the Hirota bilinear equation is
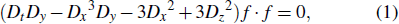
which is equivalent to
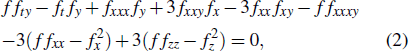
where
f =
f(
x,
y,
z,
t), and the
D-operator is defined by
[39,40]
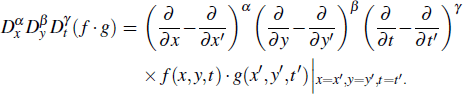
Based on the theories of the binary Bell polynomials and the bilinear operator, one can introduce a variable transformation
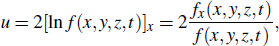
then equation (
2) is transformed into a (3+1)-dimensional model as follows:
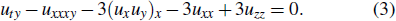
The solution
u of Eq. (
3) will be analytical when the solution
f of Eq. (
2) is positive.
This paper is arranged as follows: In Section 2, we construct a general lump solution to the reduced (3+1)-dimensional model equation. On the basis of the general lump solution, a lumpoff solution is also derived with a stripe soliton in Section 3. In Section 4, we find that the lump will become a rough wave when a pair of solitons was determined by the lump and can only visible at a specific point in time.
2. Lump solution to reduction with z = yWe first take a special reduction z = y to construct the lump solutions to the (3+1)-dimensional model equation (3). Then equation (2) turns out to be
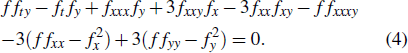
It follows that equation (
3) is converted to
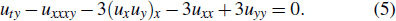
2.1. Lump solutionsTo get the single lump solution of the equivalent equation (4), we take a general quadratic function as follows:
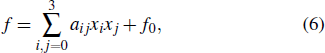
where
x1 =
x,
x2 =
y,
x3 =
t,
x0 = 1, and
aij,
i ≤
j and
f0 are constants to be determined. In Eq. (
6),
f has an expansion form as follows:
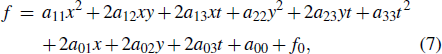
which contains eleven parameters to be determined. Substituting Eq. (
7) into Eq. (
4) and collecting the coefficients of
x,
y,
t, we obtain ten equations as follows:
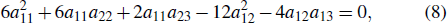
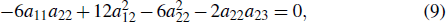
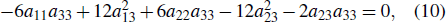
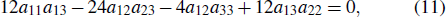
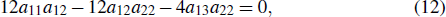

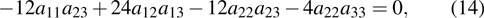
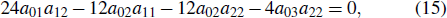
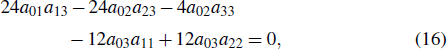
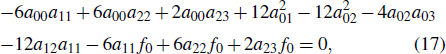
which can be used to determine the parameters of
aij and
f0. Solving Eqs. (
8)–(
17), one can get the following five constraints of
ai3 (
i = 0,1,2,3) and
f0 as
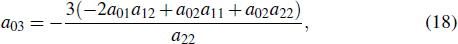




where
a01,
a02,
a11,
a12,
a22 are arbitrary constants, and
a00 is canceled out by Eq. (
22).
According to Eqs. (18)–(22), two nonzero conditions for a22 ≠ 0 and 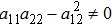 should be satisfied to find the solution to Eqs. (8)–(17).
should be satisfied to find the solution to Eqs. (8)–(17).
Substituting the result Eqs. (18)–(22) into Eq. (7), one finds

Further, we get the lump solution
u of Eq. (
5) as follows:
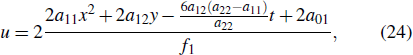
where
a01,
a02,
a11,
a12,
a22 are arbitrary constants.
Thus, the solution to Eqs. (23) and (24) containing ten parameters with five constraints and two nonzero conditions represents the general lump solutions to Eq. (3) with z = y. Next we will explore whether fewer constraints can get the similar lump solutions.
2.2. Lump solutions with more freedomTo contain more free parameters in the lump solution, we take the general quadratic function

where

with
x being a column vector matrix,
A ∈
R4 × 4 a symmetric matrix, and
f0 a positive real parameter to be determined. Here
f can be rewritten as
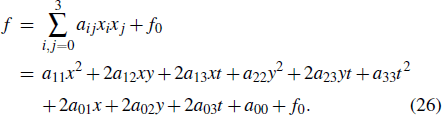
Different from Eq. (
6),
aij is redefined as
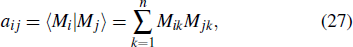
where

are
n-dimensional vectors, and
mλ,k (
λ = 1,2,…,
n and
k = 1,2,3,4) are real scalar parameters to realize.
Substituting Eqs. (26)–(28) into Eq. (4) and eliminating the coefficients of x, y, t yield two constraints as follows:
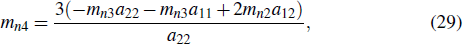
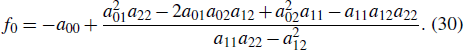
According to the above results, it is not hard to find that Eqs. (26)–(28) include infinitely many parameters. Based on the results of Refs. [3,4], n = 3 is a more right choice for general lump solutions to Eq. (3). Therefore, one can rewrite constraint conditions by taking n = 3 as

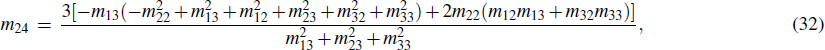


where
mλ,1,
mλ,2 and
mλ,3,
λ = 1,2,3 are real constants. Thus, we obtain the general lump solution
u of Eq. (
5) as follows:
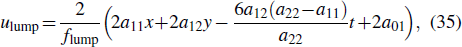
with
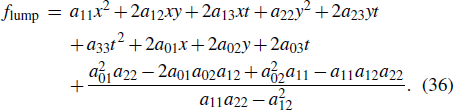
To precisely explore the moving path of lump waves expressed by Eq. (26), we give the critical point of the lump waves. Taking fx = fy = 0, the positions of the general single lump solution is

This means the lump waves move along the straight line

To further explore the propagation characteristics of lump wave (
35) in detail, we present Fig.
1 shown with the arbitrary parameters chosen as

Figure 1(a) describes the spatial structure of lump solution (35) with Eq. (39). Figure 1(b) presents the density plot of lump solution at t = 0. Figure 1(c) shows the relevant contour map of the lump solution when t = 0, t = 15 and t = 30, and the blue line expresses the propagation path (38), i.e. y = 2x.
3. Lumpoff solutionsThe interaction between lump waves and stripe soliton waves formed the lumpoff solution which is also called a cutoff lump. It means that the lump solitons can be cut by stripe solitons before or after a specific time. Therefore, we consider the lumpoff solution to the reduced (3+1)-dimensional model (3) in this section. The lumpoff solution of the reduced (3+1)-dimensional model (3) has the form as follows:
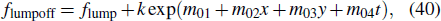
where
flump is given by Eq. (
36), and the
k,
m01,
m02,
m03 and
m04 are undetermined parameters.
Sulution (40) exhibits that the cutoff solutions composed of the lump solution and the exponential solutions. When m01 + m02x + m03y + m04 t > 0, the exponentiation part will become the dominant position. For this reason, the lump solution will only appear at m01 + m02x + m03y + m04t < 0.
Inserting Eq. (40) into Eq. (4), we have
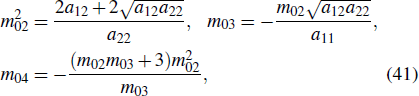
where
a11,
a12 and
a22 are defined in Eq. (
27), with
k and
m01 being arbitrary constants.
The above results show that the parameters of the soliton parts m02, m03 and m04 are related to the parameters of the bulk solution (36), i.e., a11, a12 and a22. This means that the existence of the solitons is determined by the existence of a lump. Thus, the appearance of stripe soliton coincides with lump soliton. Once the soliton is induced, the lump will be invisible until the exponential part dominates. It implies that the lump is cut off by the solitons induced by itself. We further obtain the following lumpoff solution u of Eq. (3) with z = y by the transformation u = 2(ln f)x,
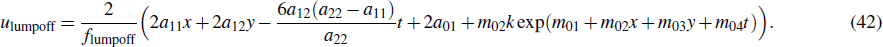
Then, a set of parameters are provided to better see the corresponding motion characteristics to lumpoff solutions to the dispersive relations in Eq. (41),
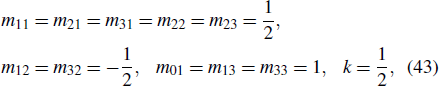
and the parameters of stripe soliton part can be given by

According to Eq. (40), we can find that the lump part is unchanged, thus the moving path of lump waves for Eq. (42) is invariable to expression in Eq. (38), one has y = 2x.
From Fig. 2, one can find the process of propagation in the space for lumpoff waves at t = −2, t = 0, t = 5, t = 20 with the selection of Eq. (44) { ,
,  ,
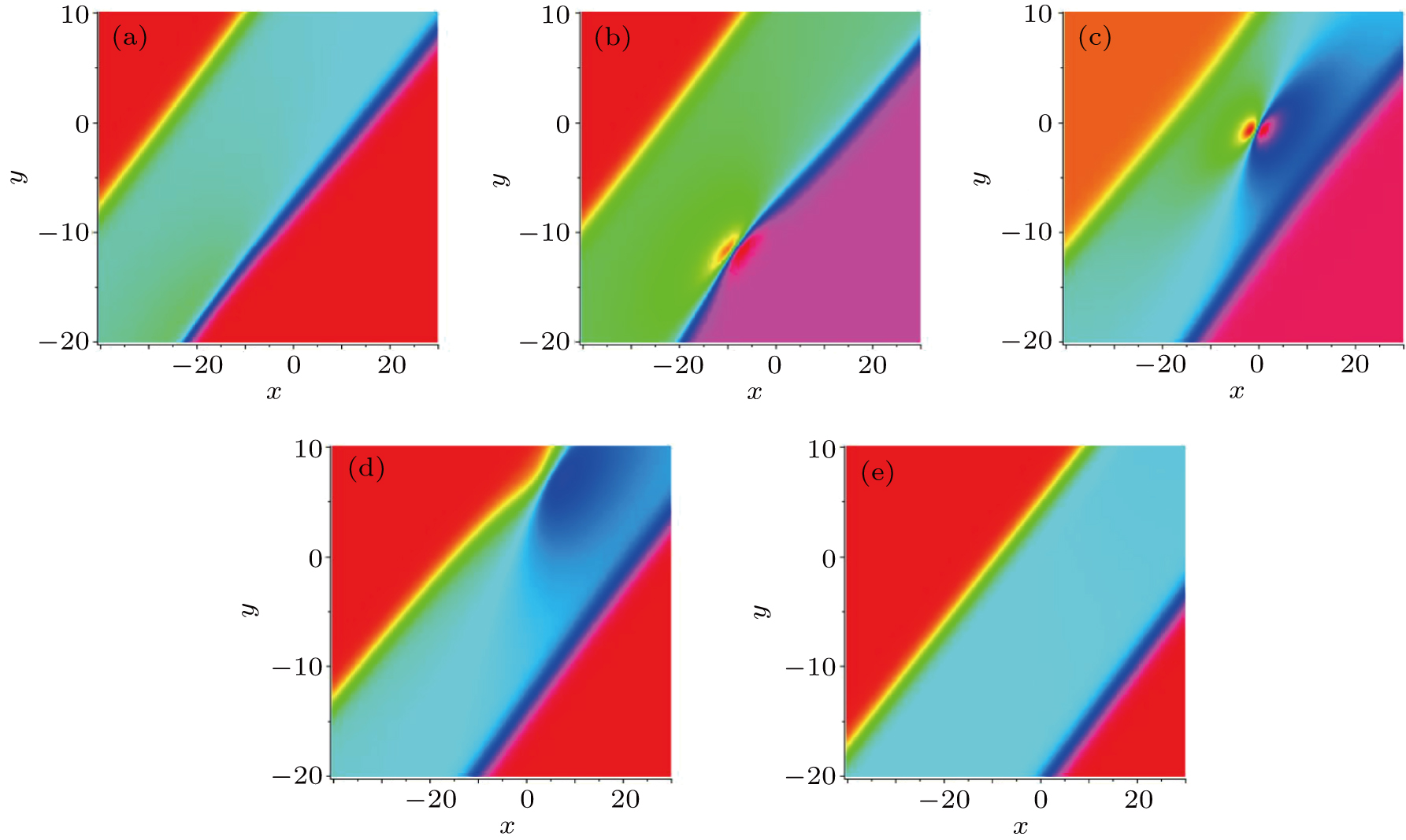
, 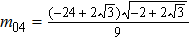 }. Additionally, Fig. 2 illustrates that the lumpoff wave is cut by the produced soliton. The lump wave appears when m01 + m02x + m03y + m04t < 0, soon afterwards the lump is cutoff by the induced soliton and eventually disappears. Figures 3(a)–3(c) display the contour plots at t = −2, t = 0, t = 5 and t = 20. Figures 3(d) and 3(e) show the relevant density plots. Moreover, the similar phenomena can be analyzed when we choose {
}. Additionally, Fig. 2 illustrates that the lumpoff wave is cut by the produced soliton. The lump wave appears when m01 + m02x + m03y + m04t < 0, soon afterwards the lump is cutoff by the induced soliton and eventually disappears. Figures 3(a)–3(c) display the contour plots at t = −2, t = 0, t = 5 and t = 20. Figures 3(d) and 3(e) show the relevant density plots. Moreover, the similar phenomena can be analyzed when we choose { ,
, 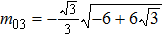 ,
,  .
.
4. Instanton/rogue wave solutionAn instanton/rogue wave is a localized wave decayed in all space and time directions. The motivation of studying predictable rogue wave is that the emerging time and place of this special rogue wave can be predicted. Thus, we focus on the instanton wave solutions to the reduced (3+1)-dimensional model (3) in this section. The instanton wave solutions of the reduced (3+1)-dimensional model (3) has the form as follows:
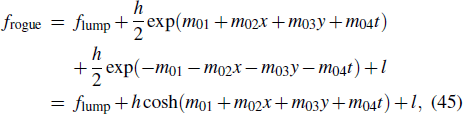
where
flump is given by Eq. (
36), the parameters
m02,
m03 and
m04 are provided by Eq. (
41),
h and
m01 are arbitrary constants, and
l is another restricted condition that will be identified by later. Based on the previous analysis, one can find that the lumpoff soliton only appears at
m01 +
m02x +
m03y +
m04t < 0, and becomes invisible for
m01 +
m02x +
m03y +
m04 t > 0. However, the lump waves are both invisible for
m01 +
m02x +
m03y +
m04t < 0 and
m01 +
m02x +
m03y +
m04t > 0 due to the existence of a pair of exponential solutions. The particular rogue waves will appear only when the lump waves move to the line
m01 +
m02x +
m03y +
m04 t ∼ 0. Substituting Eq. (
45) into Eq. (
4), collecting the coefficients and considering the restricted conditions (
41), one has

It follows that we obtain the particular rogue solution
u of Eq. (
3) with
z =
y as
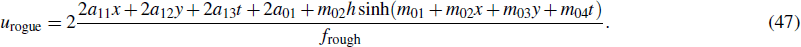
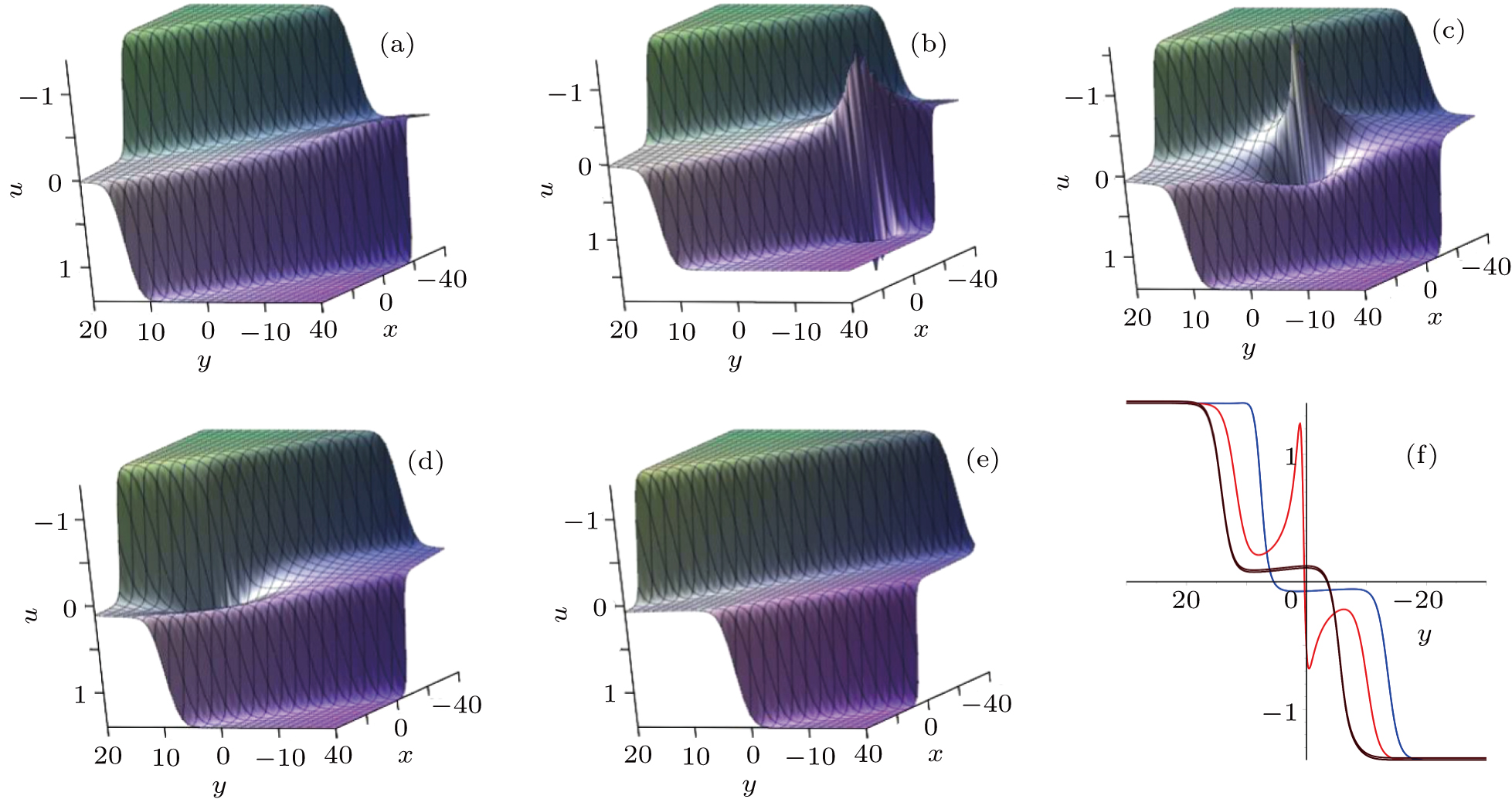
Our results show that a pair of solitons are caused by block waves. The lump wave always disappears because the cosh part being predominant, which results in the lump visible only when it moves to the line m01 + m02x + m03y + m04t ∼ 0. Then, the lump continue to move until achieve the peak at the center line m01 + m02x + m03y + m04t = 0 of a pair of resonance stripe soliton, the lump soliton becomes rogue soliton. We therefore find that the time roughly appears to read

and the position

A set of parameters is selected to explain the phenomenon of predictable rogue wave (47) as

Substituting it into Eq. (
44) yields the moving path
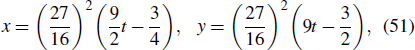
and the travelling direction

Thus, the time of the rogue waves arise at approximately t = −0.17 in (x = −4.31, y = −8.62) with arriving its peak based on Eqs. (48) and (49).
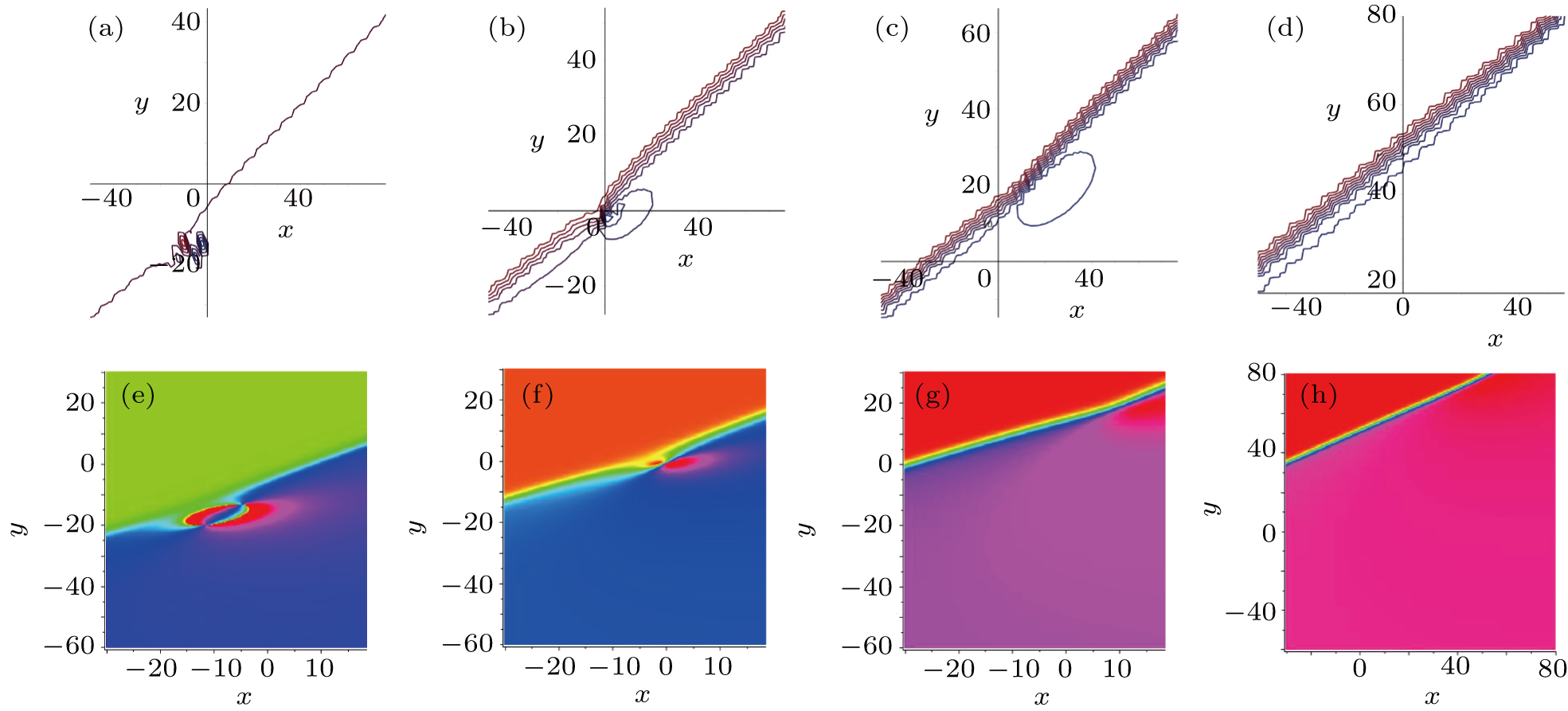
Figures 4(a)–4(e) indicate the process of propagation in the special rogue wave at different times t = −5, t = −3, t = 0, t = 2, t = 10, respectively, and panel (f) is the wave propagation along the y-axis at t = −5, t = −3, t = 0, t = 2, t = 10. Figure 5 shows the corresponding density maps of the predictable rogue wave at t = −5, t = −3, t = 0, t = 2, t = 10.
5. ConclusionIn summary, we have studied the (3+1)-dimensional model (3) with z = y, and constructed the lump solution (6) by solving the bilinear equation (4) with z = y. It follows that the more general form of lump solution is also found to contain seven arbitrary independent parameters and four constraint conditions. On the basis of the general lump solution, we find the lumpoff and instanton/rogue wave solutions. The soliton is induced by the lump as a result of lump determines a soliton, which leads to the fact that the lump will be cut and then become lumpoff. Additionally, the lump becomes a rough wave when a pair of solitons are determined by the lump, and can only be visible at a specific point of time. It is possible for us to predict the exitance of the rogue wave thanks to the existence of the visible soliton.