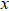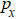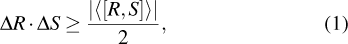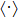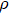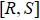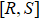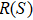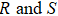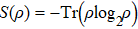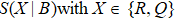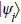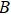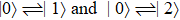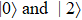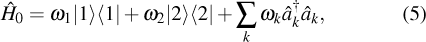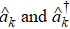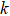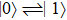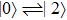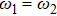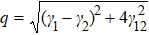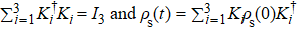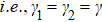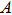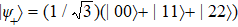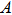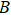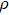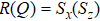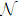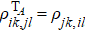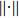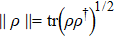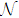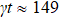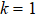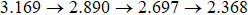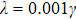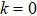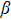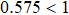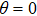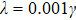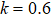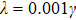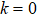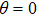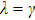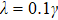Reduction of entropy uncertainty for qutrit system under non-Markov noisy environment
1. IntroductionThe uncertainty principle, originally proposed by Heisenberg, clearly illustrates the difference between classical and quantum mechanics.[1] Initially, the expression for the Heisenberg uncertainty principle with respect to the position 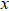 and momentum
and momentum 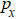 is formulated as
is formulated as  , and later was generalized by Kennard and Robertson[2] to two arbitrary observables
, and later was generalized by Kennard and Robertson[2] to two arbitrary observables  with a standard deviation
with a standard deviation
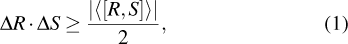
where the variance

is an arbitrary observable).
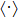
is the expectation of the observable in a quantum system
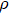
, and
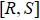
is the commutator. However, because the lower bound of the above uncertainty relation is state-dependent, the inequality will be trivial if the expectation value of the commutator
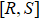
is equal to zero and the variances only contain the second-order statistical moments of the quantum fluctuations of measurements. To remove this pitfall and to obtain a more general form which is independent of the quantum state, Deutsch recast that the uncertainty can be quantified by the Shannon entropy instead of the standard deviation. After a further improvement and proof, the classical entropy uncertainty relation is defined by
[3]

where

is the Shannon entropy of the observable
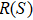
, and

is the maximum overlap of eigenvectors

corresponding to a pair of incompatible observables
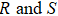
, respectively. More recently, a new entropy uncertainty relation has been derived by Renes and Boileau
[4,5] and later proved by Berta
et al.,
[6,7] which is named quantum memory assisted entropy uncertainty relation (QMA-EUR)

where

is the conditional entropy and
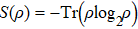
is the von Neumann entropy.
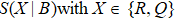
is the conditional entropy of the post-measurement state

after particle
A is measured by
X, where
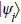
is the eigenstate of the observable
X and
I is an identity operator in the Hilbert space of particle
B. Generally, one can see the new uncertainty relation in terms of the uncertainty game between two players, Alice and Bob. Firstly Bob sends a particle

to Alice, which may entangle with his quantum memory
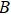
in general. Secondly, Alice measures either

and notes her outcome. Finally, Alice announces her measurement choice to Bob and Bob’s task is to minimize his uncertainty about Alice’s measurement outcome.
Recently, the improvement of this new entropic uncertainty principle as well as its dynamics have attracted increasing attention and there are potential applications such as for witnessing entanglement,[6–11] teleportation,[12] quantum phase transitions,[13] and cryptography.[14–16] In this paper, we explore the behavior of the entropic uncertainty for a qutrit system under non-Markov noisy environment. In fact, any systems are essentially open and unavoidably interact with their surrounding environment, which induces decoherence or dissipation phenomena.[17,18] Researchers usually tend to pay attention to the entropy uncertainty of qubit system. Feng et al. explored the quantum-memory-assisted entropic uncertainty relation under noises and found that the unital noises only increase the entropic uncertainty, whereas the amplitude-damping non-unital noises may reduce the entropic uncertainty in the long-time limit.[19] Fan et al. studied the relations between the quantum-memory-assisted entropic uncertainty principle, quantum teleportation, and entanglement witness.[12] Zhang et al. studied the quantum-memory-assisted entropic uncertainty principle for the qubit system in non-Markovian environments.[20] However, there are few researches on the entropy uncertainty of high-dimensional quantum systems. Quantum systems with a higher dimension may have advantages over ones with a lower dimension during quantum information processing[21,22] since they provide higher channel capacities, more secure cryptography as well as superior quantum gates.[23,24] Guo et al. studied the entropic uncertainty relation for a qutrit system under decoherence.[25] Zhang et al. studied entropic uncertainty relation of a two-qutrit Heisenberg spin model in nonuniform magnetic fields and its dynamics under intrinsic decoherence.[20] Recently, the effects of spontaneously generated interference (SGI) stimulate much interests. For instance, researchers studied the effect of SGI on absorption in a V-type system[26] and in three-level systems the nonlinear Kerr absorptions are shown to be greatly enhanced via SGI.[27] The entropy uncertainty of qutirt in non-Markovian environments has not been reported, so our work further enriches the study of the entropy uncertainty.
The paper is organized as follows. In Section 2, we present our physical model which consider a V-type three-level atom coupling to a reservoir of electromagnetic radiation modes. In Section 3, the entropy uncertainty with a memory system is investigated in non-Markovian regimes. In Section 4, we briefly discuss entropy uncertainty with SGI under non-Markovian environment. Finally, we summarize our work in Section 5.
2. Physical modelWe will consider a three-level atom which hat is in V-type atomic configuration, with states denoted as  , and
, and  , coupling to a reservoir of electromagnetic radiation modes at zero temperature.
, coupling to a reservoir of electromagnetic radiation modes at zero temperature.
In this atom, the transitions 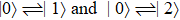 are allowed, whereas the transition
are allowed, whereas the transition  is forbidden in the electric-dipole approximation, as shown in Fig. 1; the atomic transition frequency is
is forbidden in the electric-dipole approximation, as shown in Fig. 1; the atomic transition frequency is  between atomic states
between atomic states  between atomic states
between atomic states 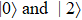 . The Hamiltonian describing the dynamics of the system in the rotating wave approximation can be written as (
. The Hamiltonian describing the dynamics of the system in the rotating wave approximation can be written as ( )
)

with
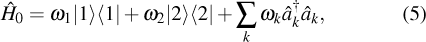

where
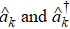
are respectively the annihilation and creation operators of the
-th reservoir, with the
-th field mode frequency
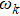
in the reservoir.

represents the coupling constants between the
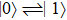
transition and the

-th reservoir. Likewise, the coupling constants between the
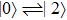
transition and the

-th reservoir is

.
Considering the atomic transition frequency 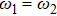 , the evolution of the atom subsystem can be obtained by Kraus operators[28] (see Appendix A for specific derivations)
, the evolution of the atom subsystem can be obtained by Kraus operators[28] (see Appendix A for specific derivations)

where

with

In this equation,

is given by

with
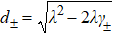
,

and
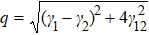
, where

is the spectral width of the distribution. When
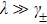
, the behavior of the system is Markovian; when

, it means the strong coupling regime and the behavior of the system is non-Markovian.

is the spontaneous decay constant of the excited sublevel
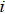
to the ground level

represents the effect of quantum interference resulting from the cross coupling between the transitions

depends on the relative angle between two dipole moment element related to the mentioned transitions.

means that the dipole moments of two transitions are perpendicular to each other corresponding to the case that there is no spontaneously generated interference (SGI) between two decay channels. On the other hand,

indicate that the two dipole moments are parallel or antiparallel corresponding to the interference effect between the two decay channels being maximal. In Eq. (
8), the unitary transformation

is given by

where

And then, using the unitary transformation

, we obtain the following expressions for


hence, it is concluded that
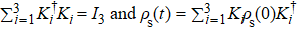
.
In this paper, we consider the relaxation rates of the two decay channels are equal, 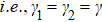 .
.
3. Reduction of entropy uncertainty for qutrit with a memory systemNow let us consider that Bob initially prepares a pair of qutrits 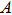 and
and  being entangled, as follows:
being entangled, as follows:

in this equation,
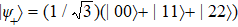
is the maximally entangled pure state. Bob sends qutrit

to Alice who measures either

on qutrit
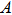
and informs Bob of her choice. Meanwhile Bob serves qutrit

as quantum memory. In this case, each part of the two qutrits locally interacts with an independent reservoir. The evolution of a two-qutrit state based on the techniques of Kraus can be characterized as
[29]

where

is Kraus operator. In this section, we choose the spin-1 observable

. The conditional von-Neumann entropy after qutrit

was measured by Alice (

) is given as follows:

the post measurement state

where

is the eigenstate of the observable

is an identity operator in the Hilbert space of particle

is the density matrix of subsystem
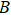
. So the left-hand side of Eq. (
3) can be given by

and the right-hand side of Eq. (
3) can be represented as
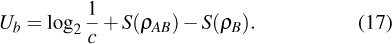

is the von Neumann entropy where
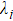
is the eigenvalue of
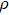
.
In the traditional entropy uncertainty relation equation (2), if we choose spin-1 observable 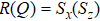 , the limit of the traditional lower bound of the entropy uncertainty can be calculated
, the limit of the traditional lower bound of the entropy uncertainty can be calculated

The degree of entanglement for qutrits system can be easily computed by the negativity
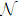
given by

The matrix  is the partial transpose with respect to the subsystem
is the partial transpose with respect to the subsystem  , that is
, that is 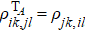 , and the trace norm
, and the trace norm 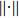 is defined as
is defined as 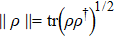 .
.
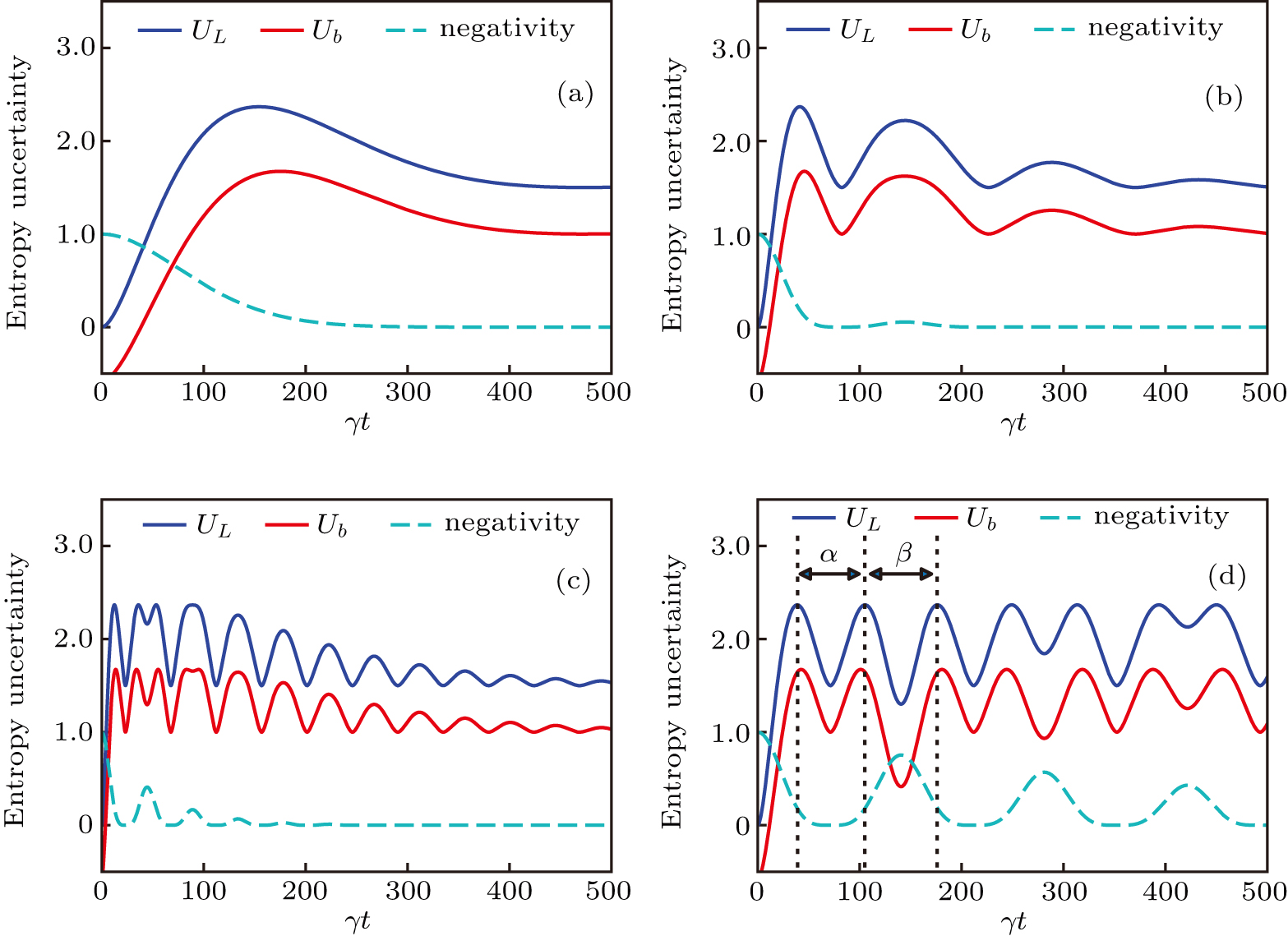
In order to study the dynamics of the entropy uncertainty for qutrits system in a non-Markov environment, we draw the change curve of the entropy uncertainty, its lower bound and the negativity 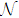 with time in Fig. 2, both of them considering the strong non-Markov case
with time in Fig. 2, both of them considering the strong non-Markov case  . In Fig. 2(a), we choose initial state as
. In Fig. 2(a), we choose initial state as  which means that two qutrits are free of entanglement and the system has no memory effects. From Fig. 2(a), on the one hand, one can see the negativity is always 0 because two qutrits are free of entanglement. On the other hand, it can be seen that the entropy uncertainty
which means that two qutrits are free of entanglement and the system has no memory effects. From Fig. 2(a), on the one hand, one can see the negativity is always 0 because two qutrits are free of entanglement. On the other hand, it can be seen that the entropy uncertainty  exhibit oscillations with the evolutionary period of
exhibit oscillations with the evolutionary period of 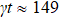 . If we select the parameter of initial state as
. If we select the parameter of initial state as  , and
, and 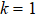 , as shown in Figs. 2(b)–2(d), there are memory effects. It is found that the entropy uncertainty and its lower limit are reduced with memory effect, by comparing Fig. 2(a) with Figs. 2(b)–2(d). The stronger strength of the initial state entanglement is, the more the entropy uncertainty reduces: from Figs. 2(a)–2(d), the maximum of the entropy uncertainty
, as shown in Figs. 2(b)–2(d), there are memory effects. It is found that the entropy uncertainty and its lower limit are reduced with memory effect, by comparing Fig. 2(a) with Figs. 2(b)–2(d). The stronger strength of the initial state entanglement is, the more the entropy uncertainty reduces: from Figs. 2(a)–2(d), the maximum of the entropy uncertainty 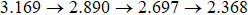 . In addition, the initial entropy uncertainty is 0 when the initial state is max entanglement which breaks the limit of the traditional lower bound of the entropy uncertainty as shown in Fig. 2(d).
. In addition, the initial entropy uncertainty is 0 when the initial state is max entanglement which breaks the limit of the traditional lower bound of the entropy uncertainty as shown in Fig. 2(d).
Figure 2(d) also reveals that, the evolutionary period of the entropy uncertainty can be divided into two regions: 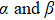 regions. Our result is different from the conventional wisdom that the entropy uncertainty is negatively correlated with entanglement. In the
regions. Our result is different from the conventional wisdom that the entropy uncertainty is negatively correlated with entanglement. In the 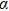 region the entropy uncertainty decreases and then slowly increases meanwhile the negativity decays asymptotically to 0 and after a freezed time, the negativity began to increase. In the
region the entropy uncertainty decreases and then slowly increases meanwhile the negativity decays asymptotically to 0 and after a freezed time, the negativity began to increase. In the  region, as the time goes the entropy uncertainty decreases with the negativity increasing and then the entropy uncertainty increases with the negativity decreasing. In other word, the entropy uncertainty is negatively correlated with entanglement in the
region, as the time goes the entropy uncertainty decreases with the negativity increasing and then the entropy uncertainty increases with the negativity decreasing. In other word, the entropy uncertainty is negatively correlated with entanglement in the  region, not in the
region, not in the  region. Beside in the
region. Beside in the  region, the minimum value of the entropy uncertainty can be reduced more. These results show that the memory systems formed by two qutrits entangled reduce effectively the entropy uncertainty and break the traditional lower bound of the entropy uncertainty when degree of the entanglement is large. In the non-Markov environment, entanglement only affects the entropy uncertainty locally and cannot completely control the evolution of the entropy uncertainty. In the
region, the minimum value of the entropy uncertainty can be reduced more. These results show that the memory systems formed by two qutrits entangled reduce effectively the entropy uncertainty and break the traditional lower bound of the entropy uncertainty when degree of the entanglement is large. In the non-Markov environment, entanglement only affects the entropy uncertainty locally and cannot completely control the evolution of the entropy uncertainty. In the 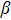 region, entanglement is beneficial to reduce entropy uncertainty.
region, entanglement is beneficial to reduce entropy uncertainty.
4. Reduction of entropy uncertainty for qutrit with SGISo far, we have only discussed the case without SGI. Next we will study the case of the strongest SGI, which means the two dipole moment elements of qutrit are parallel (or antiparallel). Figure 3 presents the numerical results of the entropy uncertainty, its lower bounds, and negativity in 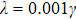 , when the two dipole moment elements of qutrit are parallel. In Fig. 3(a), we have assumed the initial state parameters
, when the two dipole moment elements of qutrit are parallel. In Fig. 3(a), we have assumed the initial state parameters 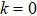 . The dynamics of the entropy uncertainty is similar to that found in the no-SGI case in Fig. 2(a), except for the evolutionary period. One can see that in the case of no memory effects, the SGI effect cannot reduce the entropy uncertainty. But if we consider the memory effects, the entropy uncertainty can be further reduced by the SGI effect. The maximum of the entropy uncertainty from 2.890 to 2.853 in the
. The dynamics of the entropy uncertainty is similar to that found in the no-SGI case in Fig. 2(a), except for the evolutionary period. One can see that in the case of no memory effects, the SGI effect cannot reduce the entropy uncertainty. But if we consider the memory effects, the entropy uncertainty can be further reduced by the SGI effect. The maximum of the entropy uncertainty from 2.890 to 2.853 in the  ; from 2.697 to 2.555 in the
; from 2.697 to 2.555 in the  , and from 2.368 to 1.596 in the
, and from 2.368 to 1.596 in the  are revealed in Figs. 3(b)–3(d). It is clearly seen that the stronger strength of the initial state entanglement is, the more entropy uncertainty can be reduced by the SGI effect. In Fig. 3(d), it should be noted that in the first
are revealed in Figs. 3(b)–3(d). It is clearly seen that the stronger strength of the initial state entanglement is, the more entropy uncertainty can be reduced by the SGI effect. In Fig. 3(d), it should be noted that in the first 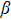 region, the minimum value of the entropy uncertainty is
region, the minimum value of the entropy uncertainty is 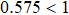 . It is lower than the limit of the traditional lower bound of the entropy uncertainty which is not found in Fig. 2(d). These results indicate that the strongest SGI can effectively reduce the entropy uncertainty in a two-qutrit entangled system.
. It is lower than the limit of the traditional lower bound of the entropy uncertainty which is not found in Fig. 2(d). These results indicate that the strongest SGI can effectively reduce the entropy uncertainty in a two-qutrit entangled system.
Finally, the influence of non-Markov strengths on the entropy uncertainty is discussed. Figure 4 shows our findings considering the initial state in maximum entanglement in the case of no SGI for different non-Markov strengths. From Fig. 4 one can see that with the non-Markov strengths increasing, the maximum value of the entropy uncertainty is not reduced, but the oscillation frequency of the entropy uncertainty increases. It is noted that with the non-Markov strengths increasing, the evolutionary period of the entropy uncertainty can be divided into two regions:  regions, as discussed in Section 3. In other word, the non-Markov effect can reduce the local minimum of the entropy uncertainty but does not affect the maximum of the entropy uncertainty.
regions, as discussed in Section 3. In other word, the non-Markov effect can reduce the local minimum of the entropy uncertainty but does not affect the maximum of the entropy uncertainty.
5. ConclusionIn conclusion, we have investigated the dynamics of the entropy uncertainty for a qutrit with and without a memory system under non-Markov noisy environment in two cases: no-SGI and the strongest SGI. We have found that the entropy uncertainty is reduced effectively with a memory system, the stronger strength of the initial state entanglement is, the more the entropy uncertainty reduces. The traditional lower bound of uncertainty is broken when degree of the entanglement is large. Furthermore, in the strongest SGI case the entropy uncertainty can be further reduced for two-qutrit entangled system. The stronger strength of the initial state entanglement is, the more entropy uncertainty can be reduced by the SGI effect. To sum up, our investigation might offer an insight into the dynamics of the entropy uncertainty in a realistic system, and it is nontrivial to quantum precision measurement in prospective quantum information processing.