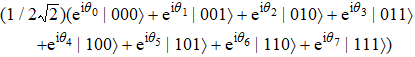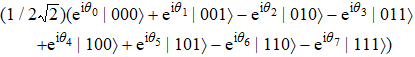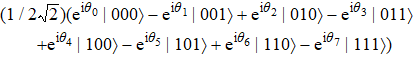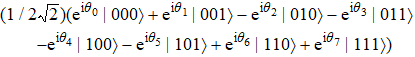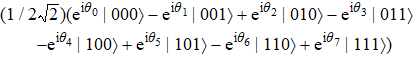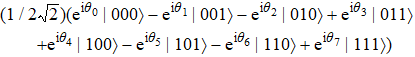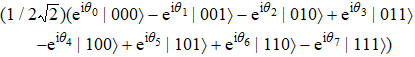† Corresponding author. E-mail:
Recently, a scheme for deterministic remote preparation of arbitrary multi-qubit equatorial states was proposed by Wei et al. [Quantum Inf. Process.
In quantum communication and quantum computation, quantum entanglement is a unique resource of the implementation. So far, some schemes have been proposed experimentally and theoretically to solve the problem of multi-mode entanglement works, such as multi-mode squeezing of parametrically amplified multi-wave mixing in atomic ensemble or atomic-like medium.[1–4] Quantum communication technology is considered as an important technology in the field of quantum information, such as quantum teleportation (QT),[5–12] remote state preparation (RSP),[13–26] quantum key distribution (QKD),[27–29] and so on. In RSP, the sender can transmit a known state to the receiver and it has less classical communication cost than QT. In order to improve the security in RSP, a variety of schemes of controlled RSP (CRSP),[30–37] joint RSP (JRSP),[38–48] controlled bidirectional RSP (CBRSP),[49–53] and controlled JRSP (CJRSP)[54–56] are presented.
In recent years, many protocols have been proposed for preparing equatorial states. In 2011, Chen et al.[57] proposed a probabilistic joint remote preparation of a two-particle high-dimensional equatorial state. In 2015, Choudhury et al.[58] presented a joint RSP scheme for preparing two-qubit equatorial states. At the same year, a scheme for joint remote preparation of multi-qubit equatorial states was proposed by Li et al.[59] A year later, Wei et al.[60] proposed a deterministic RSP scheme to remotely prepare arbitrary multi-qubit equatorial states. Recently, Sun et al.[53] realized an asymmetric bidirectional transmission of two- and four-qubit equatorial states synchronously.
Inspired by some RSP schemes in Refs. [53,58–60], we present a scheme for remotely preparing arbitrary multi-qubit equatorial states from the sender Alice to the receiver Bob, in which n two-qubit maximally entangled states are used as the quantum channel. The characteristics of our scheme is that we find a simple form of measurement basis to realize the RSP.
The rest of this paper is organized as follows. In Section
In order to interpret our protocol better, now we begin to realize the remote preparation of arbitrary n-qubit equatorial states. Suppose there are two participants named Alice and Bob, the former is the sender and the latter is the receiver, who are situated in separated sites. Presume that Alice wants to help Bob prepare arbitrary n-qubit equatorial states. Generally, it has the form as given below
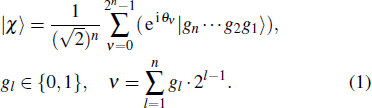
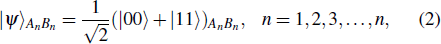
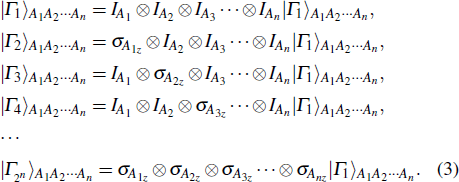
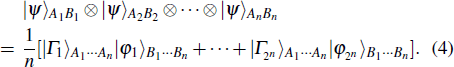
It can be obtained from the permutation and combination calculation formula that when Alice wants to help Bob prepare arbitrary n-qubit equatorial states, the possibility of σz appearing in the measurement bases can be presented as
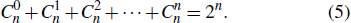
In order to show the clarity of our protocol, meanwhile, we discuss the remote preparation of three-qubit and four-qubit equatorial states respectively.
Suppose the sender Alice would like to help the receiver Bob prepare the following three-qubit equatorial state

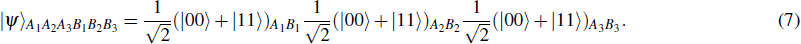
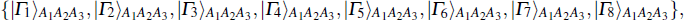
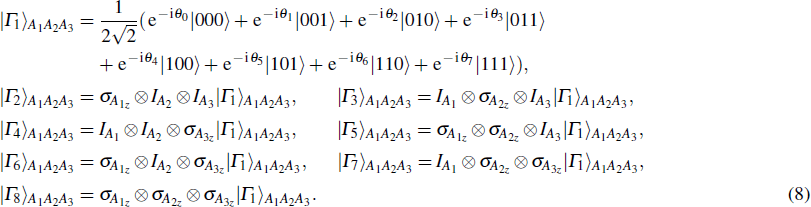
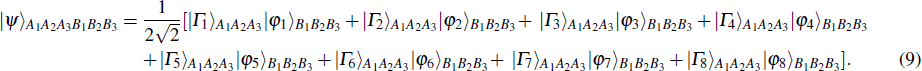
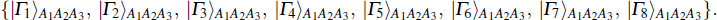
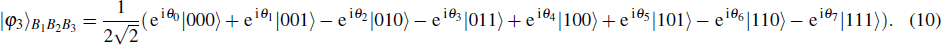
| Table 1. The measurement outcomes of Alice, Bob’s collapse states and the unitary operators of Bob. . |
Suppose that Alice wishes to prepare a four-qubit equatorial state for Bob, which can be written as
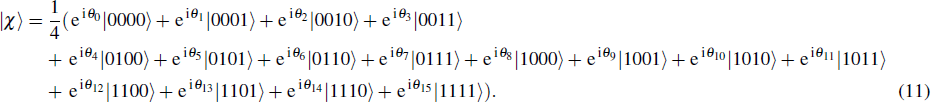

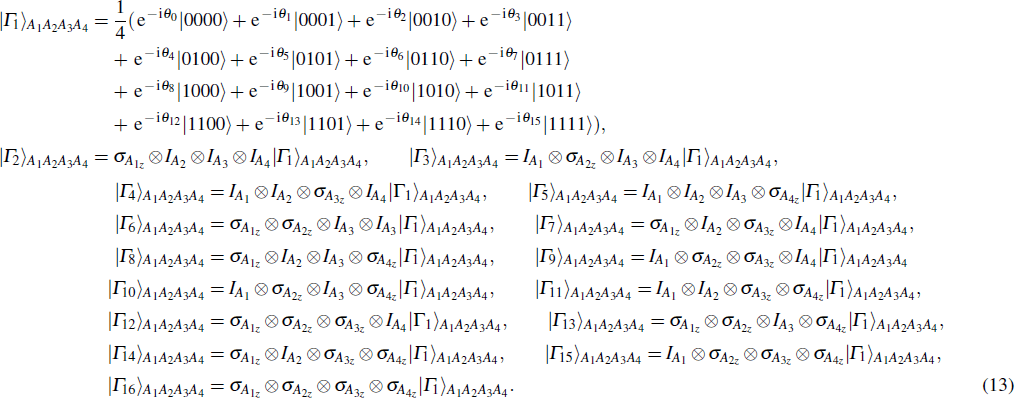
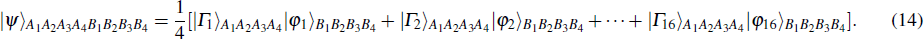

| Table 2. The measurement outcomes of Alice, Bob’s collapse states and the unitary operators of Bob. . |
In this scheme, we give a new way by utilizing n two-qubit maximally entangled states as the entangled quantum channel to prepare arbitrary n-qubit equatorial states, the probability of success can be reached 100%. Compared with the other schemes,[53,57–60] our scheme makes remote preparation of arbitrary equatorial states more simple and convenient for simplifying the measurement basis and unitary transformations in our protocol. Additionally, our scheme has no coefficient constraint and auxiliary qubits. So the success probabilities in our scheme are independent of the coefficients of the entangled channel. Furthermore, we analysis the possibility of σz appearing in the measurement bases. It will be helpful for the following study of equatorial states. In addition, our scheme is demonstrated by theoretical knowledge and concrete instances. The protocol also has greatly improved the efficiency, because of needing fewer appropriate unitary transformations to get the desired state. Thus, we wish our scheme will be realized by experiment in future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] |