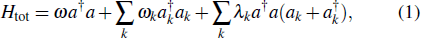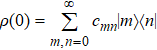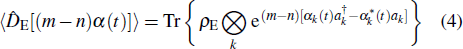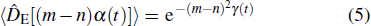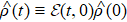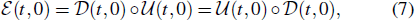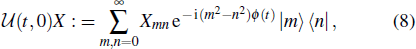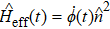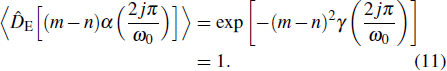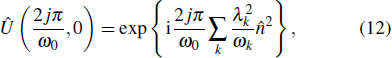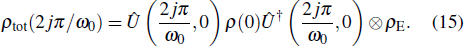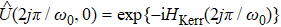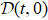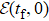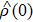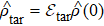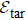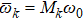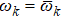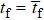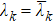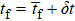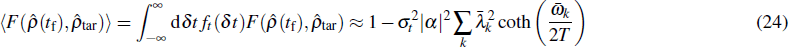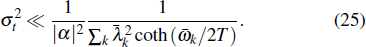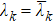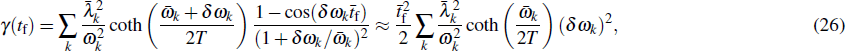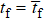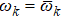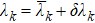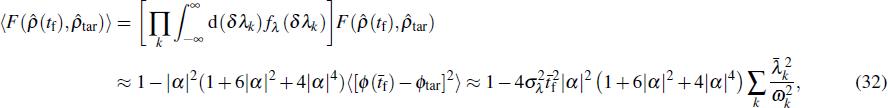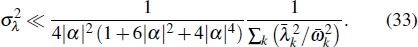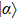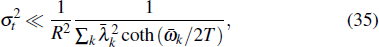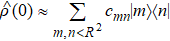1. IntroductionAs one of the typical nonlinear effects, Kerr effect[1] is related to several important physical concepts, such as optical solitons,[2,3] self-focusing,[4] and also to some implementations, e.g., all-optical switching[5] and frequency combs.[6,7] Recently, the Kerr effect has also been employed in quantum information processing for performing continuous variables operations,[8] building controlled-NOT gates,[9–11] generating non-classical states,[12–15] and realizing quantum non-demolition measurements.[16,17]
Conventional approaches for obtaining Kerr nonlinearity use the nonlinear media,[18] or combine with strong coherent states.[19,20] In Refs. [21,22], the authors have proposed schemes for generating Kerr nonlinearity and the Schrödinger-cat-like state using the well-known optomechanical interaction. Other methods include employing the technology of electromagnetically induced transparency,[23,24] or using the unique N-type level-structure of quantum systems, e.g., the superconducting qubit system,[25,26] and the diamond nitrogen-vacancy-center spin ensembles.[27]
In this paper, we aim to generate Kerr nonlinearity in a new way, i.e., with the assistance of an engineered non-Markovian environment. Although a quantum system coupled to its environment usually leads to the decoherence effect,[28,29] a non-Markovian environment could induce recoherence due to the information flowing back to the system.[28–31] Such an available feature can be exploited to generate entanglement,[32–36] build quantum memory,[36] accomplish quantum simulation,[37] and preserve quantum coherence for open systems.[38,39] Inspired by these progresses, in the present work, we aim at generating Kerr nonlinearity by coupling the system of interest to an engineered non-Markovian environment.
The system under our consideration is a bosonic mode coupled to an engineered environment composed of several noninteracting bosonic modes. The Hamiltonian of the total system is written, in units of ħ = 1, as follows:[40]
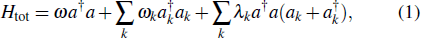
where
HS =
ωa†a is the system Hamiltonian;

and

represent the environment and the system–environment interaction, respectively. Parameters
ω and
ωk are single-particle energies of the system and the
k-th environmental mode, respectively,
a (
a†) is the annihilation (creation) operator of the system, and
ak 
stands for the annihilation (creation) operator of the
k-th mode in the environment. The real parameter
λk is the coupling strength between the system and the
k-th environmental mode. The model is a multimode extension of the well-known optomechanical interaction in Refs. [
21,
22] and we will show later that the dynamics of the system reveals strong non-Markovian nature when every
ωk is a multiple of the frequency
ω0. In this case, the map of the system’s state from
t = 0 to 2
jπ/
ω0 (
j is a positive integer) is unitary, indicating that the structured environment and the selected evolution time could realize complete information backflow
[40] and preserve coherence of the system. In the interaction picture, the unitary map equals exp{−i
HKerr(2
jπ/
ω0)}, where
HKerr =
χ(
a†a)
2 denotes the Kerr Hamiltonian with
χ characterizing the nonlinearity strength.
[13] Therefore, by taking advantage of the non-Markovian effects, our scheme can generate Kerr nonlinearity stroboscopically.
This paper is organized as follows. We solve the model exactly in Section 2, and then we demonstrate in Section 3 how to reach Kerr nonlinearity utilizing the engineered environment. In Section 4, we explore the experimental conditions that should be satisfied in fulfilling our task. A brief conclusion is given in Section 5. Some deduction details can be found in the Appendix A.
2. Exact dynamics of the systemOur purpose is to find a specific transformation imposed on the system due to coupling to the environment. To this end, we should first solve the dynamics of the system.
Without loss of generality, we assume that the total system is initially prepared in ρtot(0) = ρ(0) ⊗ ρE with 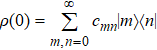 and ρE denoting the initial state of the environment (without specific mention, we suppose ρtot(0) falls into this category in the following text). In the interaction picture, the density operator of the total system evolves as
and ρE denoting the initial state of the environment (without specific mention, we suppose ρtot(0) falls into this category in the following text). In the interaction picture, the density operator of the total system evolves as  , where
, where  is the time-evolution operator in the interaction picture (see Appendix A for more details). By tracing over the environmental state in
is the time-evolution operator in the interaction picture (see Appendix A for more details). By tracing over the environmental state in  , we obtain the system’s density operator as
, we obtain the system’s density operator as  with the form
with the form

where

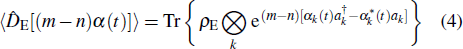
with

Note that for
m =
n,

is the identity operator of the environmental Hilbert space, and thereby the factor

reduces to 1 when
m =
n. That is to say, the diagonal elements of
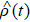
do not evolve with time, which implies that the system simply undergoes a pure-dephasing process.
To give an explicit example of the solution, we assume that the environment is initially in thermal state with temperature T. In this case,
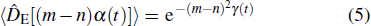
with

characterizing the phase damping dynamics. Hereafter, we set the Boltzmann constant
kB ≡ 1 for simplicity. Note that the phase damping exponent
γ(
t) considered here is quite similar to that in the spin-boson pure-dephasing model.
[28] Therefore, when the environment spectrum is continuous, the decoherence dynamics considered here is similar to that discussed in Ref. [
28]. When the spectrum of the environment is discrete,
γ(
t) could be highly oscillatory. As a result, the off-diagonal elements of

evolve non-monotonically, which is a signature of quantum non-Markovianity.
[41] As shown in the next section, for structured environment,
γ(
t) may even reach back to
γ(0) = 0. In this case, the phase damping vanishes at some time points, and the system state keeps its purity.
3. Generation of Kerr nonlinearityIn this section, we present our scheme of generating Kerr nonlinearity based on the system-environment interaction described by Eq. (1). Our scheme is independent of the initial state of the environment, but only requires precise control of the system-environment interaction time, the desired architecture of the environmental Hamiltonian, and the fine architecture of the system-environment interaction.
To show how to generate Kerr nonlinearity by taking advantage of quantum non-Markovianity, we employ the dynamical map  , which is defined by the relation
, which is defined by the relation 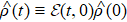 , to analyze the system dynamics. Following Eq. (2),
, to analyze the system dynamics. Following Eq. (2),  can be decomposed into the product of two maps, i.e.,
can be decomposed into the product of two maps, i.e.,
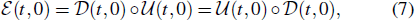
where
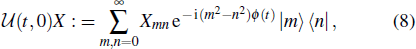

characterize the additional phase evolution and the phase damping effect, respectively. Here,

denotes an arbitrary system operator with

standing for the Fock state.
We find that  is actually a unitary transformation, whose action on an operator X has the form
is actually a unitary transformation, whose action on an operator X has the form

with

. Note that

where

is the Kerr Hamiltonian and

is the time-ordering operator. That is, the unitary part of the system dynamics can be seen as being generated by the Kerr Hamiltonian
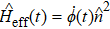
.
Following Eq. (7), one can see that generally the system–environment interaction induces both the unitary transformation and the decoherence to the system state. In order to generate the Kerr nonlinearity, one should find a scheme that eliminates the decoherence but keeps the unitary transformation at the same time.
The above task can be fulfilled by taking advantage of the facts that ϕ(t) is a monotonic function of t and  is a product of periodic functions. With engineered environment and precise control of the interaction time, one can keep ϕ(t) increasing while
is a product of periodic functions. With engineered environment and precise control of the interaction time, one can keep ϕ(t) increasing while  vanishing at particular instances. To clarify this point, we consider the case that the environment is initially prepared in a thermal state. Under the condition ωk = Mk ω0 with Mk being a positive integer, following Eq. (6), one can find that for arbitrary integer j, γ(2jπ/ω0) = γ(0) = 0, thus
vanishing at particular instances. To clarify this point, we consider the case that the environment is initially prepared in a thermal state. Under the condition ωk = Mk ω0 with Mk being a positive integer, following Eq. (6), one can find that for arbitrary integer j, γ(2jπ/ω0) = γ(0) = 0, thus
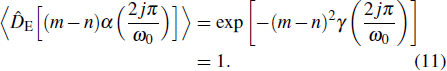
With the definition in Eq. (
9), we obtain

, which implies that the decoherence effect vanishes. In this case,

reduces to the unitary transformation described by
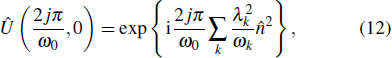
which is only relevant to the structure of the environment and the evolution time.
In the above example, the facts that  and
and  do not depend on the system’s initial state, or in another word, they are robust to the change of the environmental initial state. That is to say, whatever the system’s initial state is, thermal state or non-thermal state, if ωk = Mk ω0, from t = 0 to t = 2jπ/ω0, the dynamical map is always unitary. The property can be understood with the time-evolution operator of the total system, which reads (see the detailed derivation in Appendix A)
do not depend on the system’s initial state, or in another word, they are robust to the change of the environmental initial state. That is to say, whatever the system’s initial state is, thermal state or non-thermal state, if ωk = Mk ω0, from t = 0 to t = 2jπ/ω0, the dynamical map is always unitary. The property can be understood with the time-evolution operator of the total system, which reads (see the detailed derivation in Appendix A)

For
ωk =
Mk ω0, we obtain

which indicates clearly that
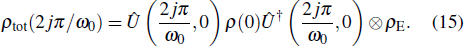
As such, from
t = 0 to 2
jπ/
ω0, the system state is transformed by the unitary operation

, and the environment state is transformed by an identity operation.
Note that 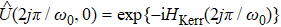 , where
, where  with
with  . This implies that, from t = 0 to 2jπ/ω0, the environment in our model introduces an operation equivalent to that induced by a medium with Kerr nonlinearity
. This implies that, from t = 0 to 2jπ/ω0, the environment in our model introduces an operation equivalent to that induced by a medium with Kerr nonlinearity

Therefore, with the structured environment interacting with the system mode through

, we could generate Kerr nonlinearity at the moments
t = 2
jπ/
ω0. From Eq. (
14), we see that this generation of Kerr nonlinearity is independent of the environmental initial state, which greatly reduces the experimental challenge under the current technology. How well our scheme works relies on the precision of the fabrication of the environment (satisfying
ωk =
Mk ω0 and the
λk’s being the desired values) and the control of the interaction time. In Section
4, we analyze the factors of imperfection, and estimate the experimental conditions required for the case that the environment is initially in a thermal state.
The dynamics considered in this paper falls into the category of boson-boson pure-dephasing dynamics, whose memory effect is studied in Refs. [40,41]. For perfect experimental conditions, the transformation of the system’s state from t = 0 to t = 2jπ/ω0 is unitary. Consequently, for two different initial states, their distinguishability at t = 0 and t = 2jπ/ω0 are the same. In the dynamics of open systems, there must be some periods during which the distinguishability between quantum states decreases, so in the case that the experimental setup is perfect, the distinguishability must evolve nonmonotonically, which is a signature of quantum non-Markovianity.[42] For imperfect experimental setup, in order to make the scheme still work well, it is required that  in Eq. (9) evolves back to near identity at specific moments. To guarantee this condition, the off-diagonal density matrix elements must evolve non-monotonically. Reference [41] has shown that this non-monotonicity is a signature of quantum non-Markovianity,[29,31] in terms of divisibility[42] and quantumness.[43]
in Eq. (9) evolves back to near identity at specific moments. To guarantee this condition, the off-diagonal density matrix elements must evolve non-monotonically. Reference [41] has shown that this non-monotonicity is a signature of quantum non-Markovianity,[29,31] in terms of divisibility[42] and quantumness.[43]
To summarize, we take advantage of ϕ(t) in  to generate the Kerr nonlinearity and the periodicity of
to generate the Kerr nonlinearity and the periodicity of 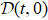 to cancel out the phase damping effects. The lose/revival of the phase information due to the property of
to cancel out the phase damping effects. The lose/revival of the phase information due to the property of  is a signature of quantum non-Markovianity.[40,41] In other words, we take advantage of quantum non-Markovianity to generate Kerr nonlinearity stroboscopically without the decoherence effect.
is a signature of quantum non-Markovianity.[40,41] In other words, we take advantage of quantum non-Markovianity to generate Kerr nonlinearity stroboscopically without the decoherence effect.
4. Experimental conditionsThe high-quality generation of Kerr nonlinearity relies on the suppression of imperfection. Here we assess the operational precision by the fidelity[44] and discuss its dependence on the imperfection of the interaction time, the environmental energy spectrum, and the system-environment coupling strength. Finally, we discuss the experimental conditions that should be satisfied in order to guarantee our scheme works well.
Generating Kerr nonlinearity means introducing the target map  ,
,

where
X is an arbitrary operator in the system Hilbert space, and
ϕtar is a real parameter, to the system of interest. For the system considered in our paper, the dynamical map in the interaction picture is

. By manufacturing the experimental system with appropriate values of
ωk and
λk, and controlling the interaction time between the system of interest and its environment, the experimentalists may construct the map
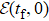
that satisfies

.
For an initial state 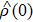 , how well the scheme works depends on the similarity between the final state obtained with our scheme, i.e.,
, how well the scheme works depends on the similarity between the final state obtained with our scheme, i.e.,  , and the target state
, and the target state 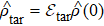 . Such similarity is usually quantified with the fidelity,[44] which we denote as
. Such similarity is usually quantified with the fidelity,[44] which we denote as  . To find out the necessary experimental conditions, from Subsection 4.1 to Subsection 4.3, we consider the explicit case that initially the system is in a coherent state
. To find out the necessary experimental conditions, from Subsection 4.1 to Subsection 4.3, we consider the explicit case that initially the system is in a coherent state  and the environment is prepared to be in a thermal state ρE = e−HE/T/Tr[e−HE/T]. More general cases, i.e.,
and the environment is prepared to be in a thermal state ρE = e−HE/T/Tr[e−HE/T]. More general cases, i.e.,  is an arbitrary physical state instead of a coherent state, are discussed in Subsection 4.4.
is an arbitrary physical state instead of a coherent state, are discussed in Subsection 4.4.
When  , the fidelity between the obtained state and the target state can be reduced to
, the fidelity between the obtained state and the target state can be reduced to

where

is the inverse of
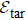
. In order to analyze the experimental conditions, in the following, we assume

where

,
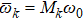
, and

are the desired interaction time, environmental energy spectrum, and interaction strength, respectively. That is, if one can control the interaction time
tf exactly equaling

, manufacture the environment satisfying exactly
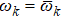
and its coupling with the system
λk is exactly

, then

,
i.e., the task is perfectly fulfilled.
However, experimental conditions cannot be perfect. Namely, the equations 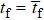 ,
,  and
and 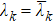 cannot be exactly satisfied. In order to make our scheme work well, i.e.,
cannot be exactly satisfied. In order to make our scheme work well, i.e.,  , the errors of tf, ωk and λk should not be large. Assume that the precision of time control, the precision of engineering on the environment energy level and the precision of tuning the interaction strength are σt, σω, and σλ, respectively. In the following three subsections, we will estimate the requirements on σt, σω, and σλ in fulfilling the task of generating
, the errors of tf, ωk and λk should not be large. Assume that the precision of time control, the precision of engineering on the environment energy level and the precision of tuning the interaction strength are σt, σω, and σλ, respectively. In the following three subsections, we will estimate the requirements on σt, σω, and σλ in fulfilling the task of generating  .
.
4.1. Precision of time controlIn this subsection, we investigate the precision of time control required in making our scheme work well.
Assume that the conditions  and
and  have been perfectly satisfied, then the imperfection can only originate from the imprecision of time control. To estimate the precision required, we assume
have been perfectly satisfied, then the imperfection can only originate from the imprecision of time control. To estimate the precision required, we assume 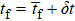 , where δt is a stochastic variable satisfying the Gaussian distribution
, where δt is a stochastic variable satisfying the Gaussian distribution  , with σt characterizing the error of the interaction time and satisfying ω0 σt ≪ 1. Following Eqs. (3), (6), and (9), γ(tf) and ϕ(tf) can be transformed to
, with σt characterizing the error of the interaction time and satisfying ω0 σt ≪ 1. Following Eqs. (3), (6), and (9), γ(tf) and ϕ(tf) can be transformed to


Together with Eqs. (
7) and (
8), we obtain

for which

is reduced to

Note that
δt is a stochastic variable, the fidelity should take the average, reading
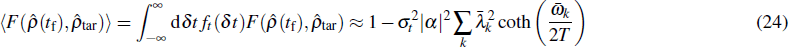
for small
σt. In order to make the scheme work well,
i.e.,

, the precision of time control should satisfy
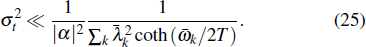
4.2. Precision of the environment energy spectrumAnother kind of error originates from the imperfect architecture of the environment, that is, not all the single-particle energies are exactly multiples of ω0. Suppose that the control of interaction time and the architecture of the coupling strengths are perfect, i.e.,  and
and 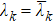 ; while ωk satisfies
; while ωk satisfies  , where δωk are stochastic variables satisfying the Guassian distribution
, where δωk are stochastic variables satisfying the Guassian distribution  , with σω characterizing the experimentalists’ ability of architecturing the environment energy level. Under the condition σω tf ≪ 1,
, with σω characterizing the experimentalists’ ability of architecturing the environment energy level. Under the condition σω tf ≪ 1,
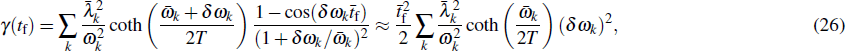
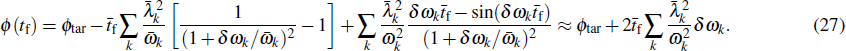
Similar to the procedure in the previous subsection, by substituting
γ(
δ t) and
ϕ(
δ t) in Eq. (
23) with
γ(
tf) and
ϕ(
tf) −
ϕtar, respectively, and taking the ensemble average, one obtains the average fidelity in this case, reading

where we leave the terms whose orders are not higher than
σω2, and the third approximation is made because the coupling between the system and environment is usually weak, namely,

. According to Eq. (
28), in order to reach a high fidelity, it is required that

4.3. Precision of the interaction strengthSuppose 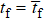 ,
, 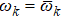 , but the coupling strengths λk are not the desired values. We assume that for every λk,
, but the coupling strengths λk are not the desired values. We assume that for every λk, 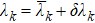 , where δλk is a stochastic variable satisfying the Gaussian distribution
, where δλk is a stochastic variable satisfying the Gaussian distribution  , with σλ characterizing the error of the coupling strengths and σλ ≪ λk. In this case, following Eqs. (3), (6), and (19),
, with σλ characterizing the error of the coupling strengths and σλ ≪ λk. In this case, following Eqs. (3), (6), and (19),


Similar to the procedure in Subsection
4.1, by substituting
γ(
δ t) and
ϕ(
δ t) in Eq. (
23) with 0 and
ϕ(
tf) −
ϕtar, respectively, and taking the ensemble average, one obtains the average fidelity in this case, reading
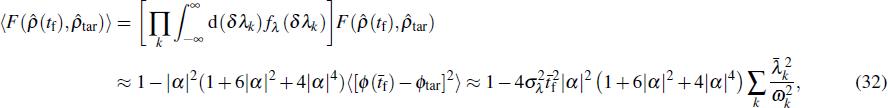
where we leave only the terms whose orders are not higher than

. In order to reach a high fidelity, the error of the interaction strength should satisfy
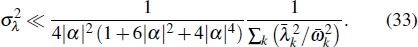
In the expression, for small |
α|, 4 |
α|
2 (1 + 6|
α|
2 + 4|
α|
4) can be approximated as 4 |
α|
2; while for large |
α|, it can be approximated as 16|
α|
6; for intermediate value of |
α|,
i.e., |
α| ≈ 1, it can be approximated as the latter of the above expressions. To summarize,
σλ should satisfy

4.4. DiscussionThe above three subsections set the experimental conditions that should be satisfied in fulfilling the task of generating Kerr nonlinearity with our scheme. Generally, the three origins of error coexist. In order to make the scheme work well, all the conditions: equations (25), (29), and (34) should be satisfied.
Even though the conditions are obtained for the case that the initial state is a coherent state, they can be generalized to more general cases. The initial state  can be expressed with the P representation, i.e.,
can be expressed with the P representation, i.e.,  .[13,45,46] Because the particle number in an experimentally feasible state
.[13,45,46] Because the particle number in an experimentally feasible state  is always finite, there must exists a bound R such that
is always finite, there must exists a bound R such that

i.e., the contribution of

to

with |
α| >
R is negligible. To guarantee that our scheme works well for such

, it is required that it works well for all the coherent states
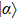
with |
α| ≤
R. Therefore, for a general
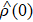
,
σt,
σω, and
σλ should satisfy
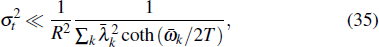


The physical meaning of
R2 can be seen more clearly in the particle number basis. Note in the
P representation,
R2 is determined with the condition

. In the particle number basis, the condition can be equivalently written as
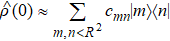
,
i.e., the components with particle number larger than
R2 can be neglected. Therefore,
R2 is the physical upper bound of the particle number initially in the system. Mathematically, the condition can be simplified, reading

To summarize this section, by assuming that the precision of time control is
σt, the precision of environment energy spectrum is
σω, and the precision of tuning the coupling strength is
σλ, we estimate that in achieving the goal of approximately generating
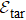
, the constraints over
σt,
σω, and
σλ can be expressed as Eqs. (
35)–(
37). The constraints are dependent on the system’s initial particle distribution,
i.e., the
R in Eqs. (
35)–(
37) satisfies Eq. (
38). The more particles the system contains initially, the tighter the bounds on
σt,
σω, and
σλ become. That is, our scheme is more demanding on the experimental conditions if the system initially contains more particles.
5. SummaryOur scheme can be implemented in the superconducting circuit system.[47,48] Since such devices have been employed to engineer strongly-correlated quantum matter, the interaction strength λk in Eq. (1) can be relatively large. As such, using our scheme, these devices could be excellent platforms for generating Kerr nonlinearity. In addition, our scheme can also be extended to both optomechanical systems[49] with suitably arranged structure and cavity arrays connected by transmission lines,[50] which have the potential to achieve the model Hamiltonian.
To summarize, we have presented a scheme for generating Kerr nonlinearity with an engineered environment, which is insensitive to the initial environmental state. Our scheme is practical for some systems without Kerr interaction or with difficulty in creating Kerr interaction directly.