Cite this Article
Shi Jin-Jing, Li Bo-Peng, Huang Duan. Reconciliation for CV-QKD using globally-coupled LDPC codes. Chinese Physics B, 2020, 29(4): 040301  
Permissions
Reconciliation for CV-QKD using globally-coupled LDPC codes
Shi Jin-Jing, Li Bo-Peng, Huang Duan †
School of Computer Science and Engineering, Central South University, Changsha 410083, China

 

† Corresponding author. E-mail: duanhuang@csu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61801522, 61972418, and 61872390), the Natural Science Foundation of Hunan Province, China (Grant Nos. 2019JJ40352 and 2017JJ3415), and the Special Foundation for Distinguished Young Scientists of Changsha City, China (Grant No. kq1905058).

Abstract

Reconciliation is a necessary step in postprocessing of continuous-variable quantum key distribution (CV-QKD) system. We use globally coupled low-density parity-check (GC-LDPC) codes in reconciliation to extract a precise secret key from the raw keys over the authenticated classical public channel between two users. GC-LDPC codes have excellent performance over both the additive Gaussian white noise and binary-erasure channels. The reconciliation based on GC-LDPC codes can improve the reconciliation efficiency to 95.42% and reduce the frame error rate to 3.25 × 10–3. Using distillation, the decoding speed can achieve 23.8 Mbits/s and decrease the cost of memory. Given decoding speed and low memory usage, this makes the proposed reconciliation method viable approach for high-speed CV-QKD system.

PACS: ;03.67.-a;;03.67.Dd;;03.67.Hk;;03.67.Pp;
Keyword:;continuous-variable quantum key distribution;;globally coupled low-density parity-check;;reconciliation efficiency;;frame error rate;
1. Introduction

Quantum key distribution (QKD)[1] system allows two legitimate parties Alice and Bob, linked by a quantum channel and an authenticated classical channel, to share a common random binary key that is unknown to a potential eavesdropper, Eve.[2] The security of QKD is guaranteed by the no-cloning theorem of quantum mechanics. The no-cloning theorem considers that Eve measuring or observing quantum channels would disturb the coherent state which is transmitted from Alice to Bob.[3,4] There have been increased experimental efforts recently in QKD to prove the safety of QKD.[5–7] Continuous variable (CV) and discrete variable (DV) are two major types of QKD system. DV-QKD protocols encode information on the phase or the polarization of single photons.[8] Many schemes are proposed for DV-QKD systems,[9,10] and some of them have been explored to realize long distance and high secure key rate.[11,12] In information reconciliation process, we use low-density parity-check (LDPC) codes to reduce the information which Eve obtains from the honest parties Alice and Bob.[13,14] In CV-QKD system, Alice encodes her information in the amplitude and phase quadrature of coherent states[15,16] and sends it to Bob. On his side, Bob measures the quantum states using homodyne or heterodyne detector.[17,18] The CV-QKD provides a higher repetition rate, which provides a scheme to achieve a higher security key rate.[19]

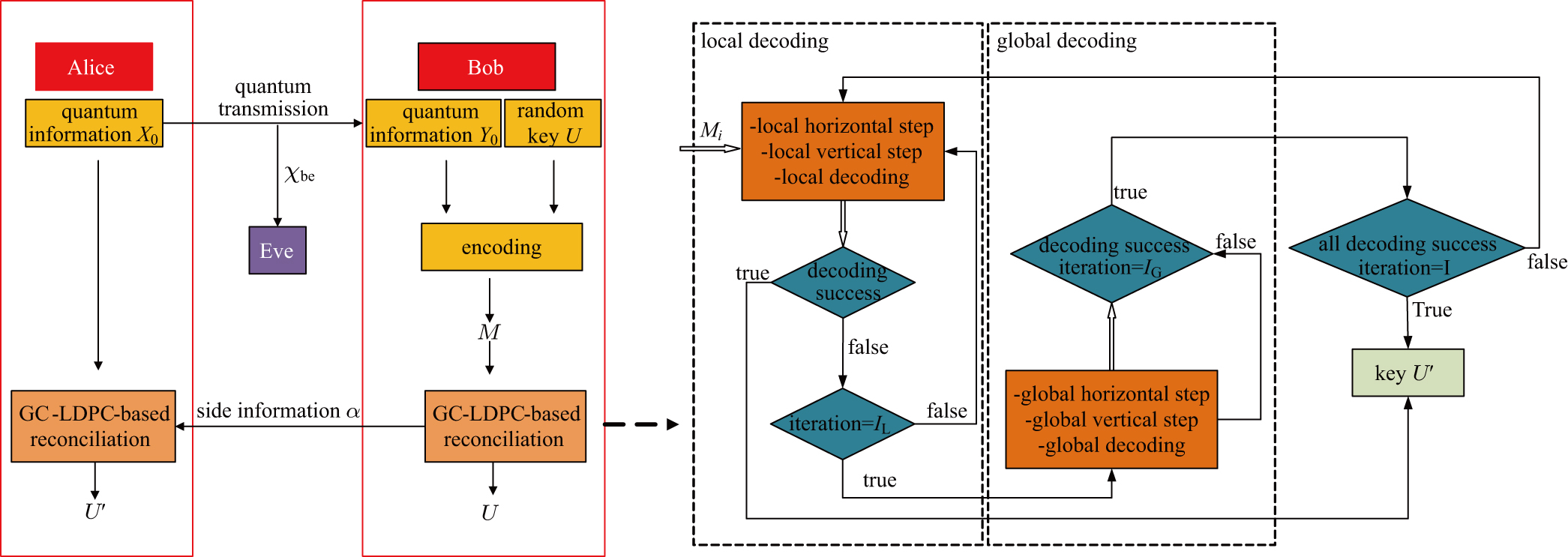
In CV-QKD, the quantum channel used by Alice and Bob to create secret key is not deemed to be prefect. Noise will make the secret key different between Alice and Bob.[20,21] The information between Alice and Bob, along with the information which Eve gains by monitoring the reconciliation protocol, must then be corrected via post-processing. The post-processing of the CV-QKD system includes the following steps: sifting,[22] parameter estimation,[23,24] information reconciliation,[25] and privacy amplification.[26–29] The post-processing procedure is used to extract final secret key from the obtained raw key,[30] and the information reconciliation is used to correct the errors between Alice’s and Bob’s raw keys by exchanging error correcting messages through an authenticated classical channel.[31] We use LDPC codes to complete information reconciliation in our scheme. There are two types of information reconciliation, i.e., direct reconciliation and reverse reconciliation.[32] Direct reconciliation is that Bob corrects its codeword based on Alice, while reverse reconciliation is that Alice corrects its codeword based on Bob. Due to the safe transmission distance cannot exceed the 3-dB limitation during direct reconciliation, only reverse reconciliation is considered in all safety considerations at this stage.

In order to improve the efficiency of information reconciliation[33,34] for the additive white Gaussian noise channel, we complete reverse reconciliation using check node-based quasi-cyclic globally coupled low-density parity-check (CN-based QC-GC-LDPC) codes which decrease the frame error rate (FER) of CV-QKD. Improving the efficiency can increase the secret key rate. CN-based QC-GC-LDPC codes have a different structure compared to the conventional LDPC block codes and the spatially coupled LDPC (SC-LDPC) codes. Reverse reconciliation[35–37] based on GC-LDPC codes can provide higher reconciliation efficiency than other block codes. After distillation, the decoding speed of reverse reconciliation can reach 23.8 Mbits/s. Through the simulation of our scheme, we obtain the reconciliation efficiency of CN-based QC-GC-LDPC codes can reach 95.42%. Reverse reconciliation using GC-LDPC codes also reduce the FER of CVQKD system, the FER can reach 3.25 × 10–3 and the bit error rate (BER) can be reduced to 5.45 × 10–7. These will make the proposed scheme have high reconciliation performance.

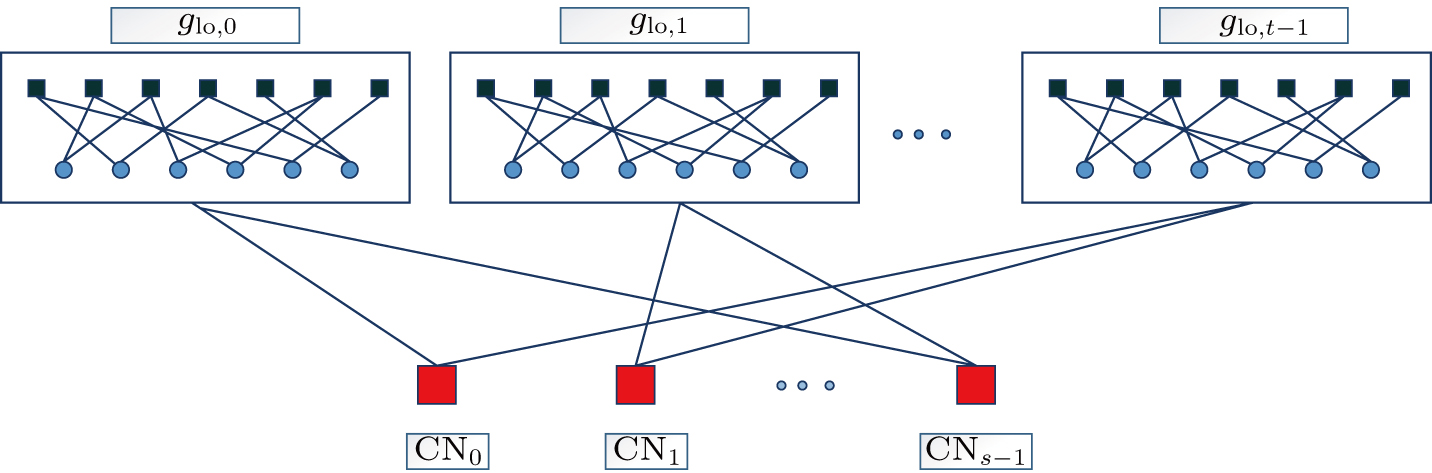
The paper is arranged as follows: In Section 2, after brief introduction on GC-LDPC, we introduce the CN-based QC-GC-LDPC codes, and then we present the reconciliation scheme based on CN-based QC-GC-LDPC codes in Subsection 2.2. In Subsection 2.3, we discuss the decoding of CN-based QC-GC-LDPC code scheme in CV-QKD system. The performance of reverse reconciliation based on CN-based QC-GC-LDPC codes is given in Section 3, which includes high decoding speed method, low frame error rate, and high reconciliation efficiency. Finally, conclusion are drawn in Section 4.

2. Reconciliation based on CN-based QC-GC-LDPC codes

CN-based QC-GC-LDPC codes, which were proposed by Li et al. in Ref. [38], are a special type of LDPC codes with a structure related to but different from that of the SC-LDPC codes. From the perspective of Tanner graph, GC-LDPC codes are composed of a series of disjoint Tanner graphs which are connected together by a group of overall check-nodes (CNs), called global CNs. LDPC codes with this type are called CN-based QC-GC-LDPC codes, which have excellent performance in both the additive white Gaussian noise channel (AWGNC) and the binary erasure channel (BEC).

2.1. CN-based QC-GC-LDPC codes

CN-based QC-GC-LDPC codes are a kind of quasi-cyclic linear block codes. They are defined by their sparse parity check matrices H = (hij)m×n of size m × n where hij are elements of a binary Galois field GF(2) or non-binary Galois field GF(q) where q > 2. The construction method of CN-based QC-GC-LDPC codes has been introduced in detail in Ref. [39]. Here we briefly introduce the structural characteristics of CN-based QC-GC-LDPC codes. A CN-based QC-GC-LDPC codes are composed of base matrix Bgc which consists of two submatrices as shown:

The above submatrix of Bgc is a diagonal matrix of size t × t and Bgc is consisted by diagonal array which includes (m × n)-dimensional matrices R and the lower submatrix is matrix Xgc, where the form of R are derived from Reed–Solomon-based array and the matrix Xgc is an (s × nt)-dimensional matrix. The matrix Bgc and Xgc represent “check node” and “global coupling”, respectively.

Denote the parity-check matrix of CN-based QC-GC-LDPC codes as Hqc,gc as shown in Eq. (2). Hqc,gc is made up of the base matrix Bgc and (q − 1)-fold dispersion.[40] In Bgc matrix, if its element bi,j = 0, we replace bi,j with a (q − 1) × (q − 1) zero matrix (ZM); otherwise, if bi,j ≠ 0, we replace bi,j by a (q − 1) × (q − 1) circulant permutation matrix (CPM).[41]

Same as other types of LDPC codes, CN-based QC-GC-LDPC codes can also be represented by Tanner graphs as shown in Fig. 1. Its Tanner graphs are divided into two parts, t disjoint copies of the local Tanner graphs glo and s global check nodes respectively. The s global check nodes provide the only connections between any two disjoint local Tanner graphs.

Fig. 1. The Tanner graphs of CN-based QC-GC-LDPC codes. The upper t disjoint copies are local Tanner graphs and the lower s check nodes are global check nodes which provide the only connections between the t disjoint local Tanner graphs.
2.2. Reconciliation based on CN-based QC-GC-LDPC codes

In CV-QKD system, Alice transmits N quantum coherent states to Bob through a quantum channel,[42] i.e., y0 = t × x0 + z, where , where ηloss is detection efficiency and T is the transmission efficiency, and z is the noise term subjecting to a centered normal distribution with a zero mean and noise variance of . Alice’s and Bob’s data are different due to imperfection of quantum channel. The main reason for imperfection is the existence of noise. After exchanging some quantum states on the quantum channel, Alice and Bob share some common data to complete the information reconciliation process. In order to complete the reverse reconciliation, Alice and Bob construct two new correlated Gaussian sequences from the sifted correlation sequences X0 = [x1, x2, …, xquantum] and Y0 = [y1, y2, …, yquantum] of length Nquantum. Alice and Bob select a set of elements U of length n, which n < Nquantum. In addition, n is equal to the LDPC codes block length.[15] The string U is selected as the secret key which will be transferred between Alice and Bob.[43]

As shown in Fig. 2, when Alice sends quantum information X0 through a quantum channel, the string Y0 received by Bob will be correlated to X0 but not equal to X0 due to the existence of channel noise. We correct the sequence X0 according to the sequence Y0 using the reverse reconciliation. Bob modulates the quantum information Y0 to get M using random key U. Then Bob sends side information α to Alice to describe the method of obtaining M. Alice receives the side information α and applies α to X0 to get U′, where U′ can be regarded as a noisy version of U. Alice and Bob reconstruct U′ and U using the computationally intensive Sum-Product belief propagation decoding algorithm (BP algorithm) respectively.[44,45] The reverse reconciliation is described in detail in Subsection 2.3.

Fig. 2. The reverse reconciliation based on GC-LDPC codes provide the secondary reconciliation for the CV-QKD system, which can reduce the FER and BER. Using GC-LDPC codes can improve the performance of CV-QKD.
2.3. Decoding of CN-based QC-GC-LDPC codes in reverse reconciliation

We mentioned the BP algorithm in Subsection 2.2. In this section we will describe the decoding algorithm for the reverse reconciliation protocol[46,47] in detail. In CV-QKD system, Alice uses the BP algorithm to correct the classic messeage M over an optic fiber, where Mi = (−1UiY0i). Considering structural characteristics of CN-based QC-GC-LDPC codes, the decoding process is divided into two parts: local decoding and global decoding. The received data M divides t sequences and decoded by t-independent decoders. If t sequences are decoded successfully and the locally decoded codeword U satisfies constraints of the parity-check Hqc,gc, i.e., , the codeword U could be delivered to remove the channel noise from her received message M, where is the transposed matrix of the matrix Hqc,gc. If local decoders encounter error during the decoding process, i.e., , we switch the decoding from the local part to global part through the global check nodes. In general, the global decoders are needed only when the amount of error in local decoding is large.

In the BP decoding algorithm, the quantities of non-zero elements in check nodes (CNs) and variable nodes (VNs) are constantly updated during the iteration. The operations of message passing can be described as follows:[48]

Step 1 Initialization

where xl = 0 means the prior probability of bit x1 in received data is 0.

Step 2 Horizontal step

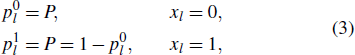
In the horizontal step, we calculate message L(rji) of each CN which passed from CNs to VNs. This step is used to update message of CNs.

where rji is the message passed from CNs to VNs, qi′j is the message passed from VNs to CNs, tanh(·) is the hyperbolic tangent function, and tanh–1(·) is the reverse hyperbolic tangent function. In addition, Rj is the set of column positions of element 1 in the j-th row of matrix H, Rj\i is the set of column positions of element 1 in the j-th row of matrix H excluding position i.

We depict the CN decoder situation in Fig. 3. Note that the CNj decoder receives message from the channel and the variable nodes connected to it, excluding the message from VNi. After calculating these message using Eq. (4), CNj sends L(rji) to VNi.

Fig. 3. Figure of the horizontal step. The message Lrji is calculated based on information from all of its variable nodes, excluding message from VNi, and message L(rji) is sent to VNi.

Step 3 Vertical step

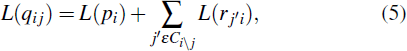
In this step, we calculate message L(qij) of each VN which passed from VNs to CNs. In Fig. 4, we describe the process of information update about VNs in detail. This process includes calculating the message from the channel and the check nodes connected to it excluding the message from CNj. After calculating these message using Eq. (5), VNi sends message L(qij) to CNj.

where Pi is initialized decoding information. L(rji), L(qij), and L(Pi) are the log-domain versions of rji, qij, and Pi. Similarly, Ci is the set of row locations of element 1 in the i-th column, and Ci\j is the same as Ci, expect that location j is not included.

Fig. 4. This figure shows the vertical step. The message L(qij) is calculated based on information from all of its check nodes, excluding message from CNj, and message L(qij) is sent to CNj.

Step 4 Decoding

If pi × Ht = 0 or the number of iterations equals the maximum limit, stop; else, go to Step 2.

3. Performance of reverse reconciliation based on CN-based QC-GC-LDPC codes

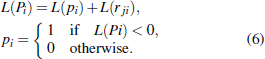
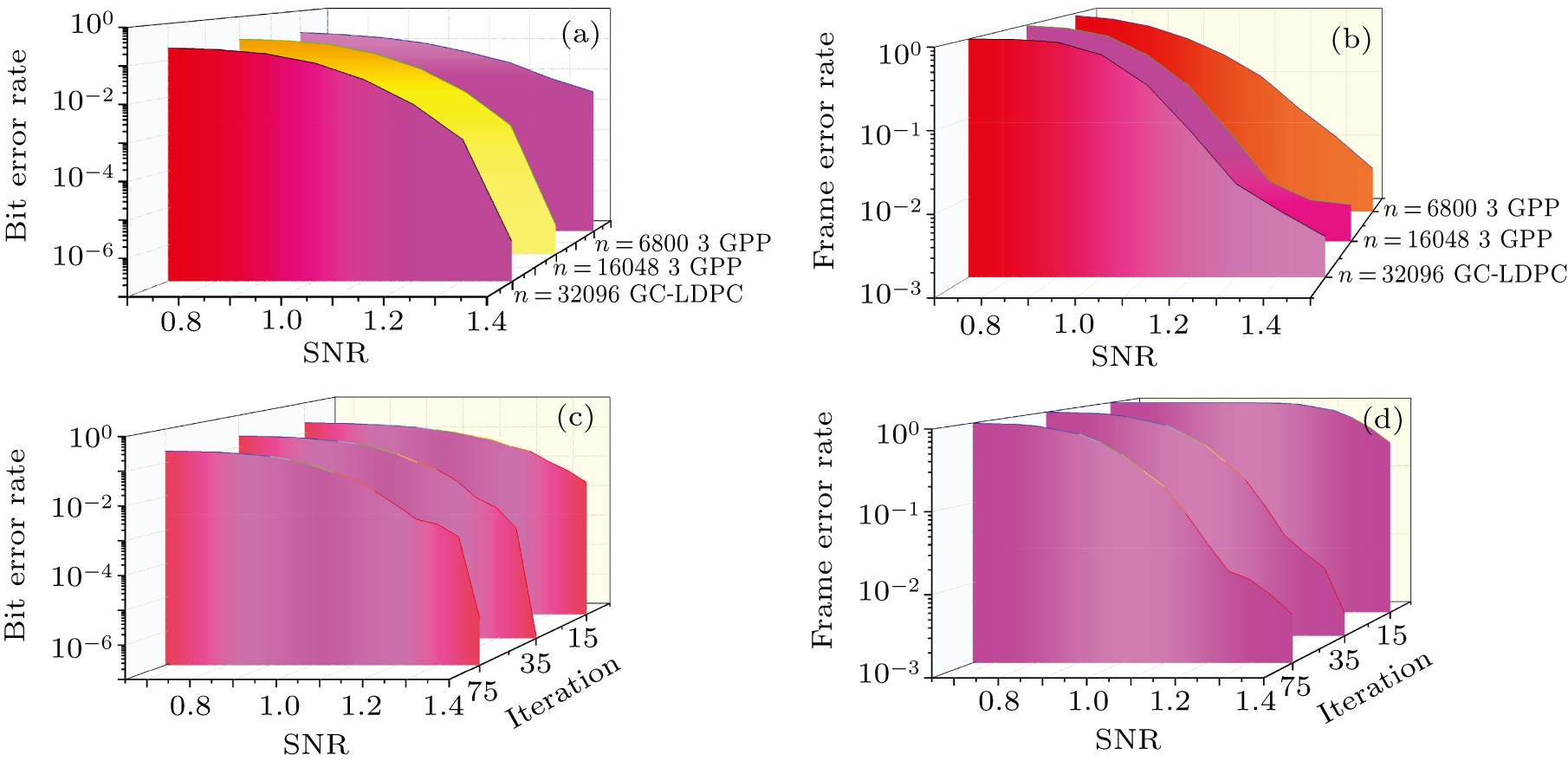
In this section, we will introduce the performance of reverse reconciliation based on CN-based QC-GC-LDPC codes. There are some indicators that can reflect the performance of the reverse reconciliation, such as bit error rate, frame error rate, decoding speed, and reconciliation efficiency β.

3.1. The speed of decoding

In order to achieve high speed of the reverse reconciliation, it is necessary to analyze the factors which affect the reconciliation speed. Some factors will affect the reconciliation speed in different aspects, such as the decoding algorithm. The decoding algorithm is the most important factor affecting the reconciliation speed, and it is also the most important step of the reverse reconciliation. We use the BP algorithm to complete the reverse reconciliation. We apply the check matrix Hqc,gc in the BP algorithm and the sparsity and irregularity of the check matrix bring the difficulty in calculation and decoding.

Considering the sparsity of the check matrix Hgc,qc, we apply “distillation” to reduce the complexity of the operation about the error correction.[4] Since the decoding process of BP algorithm is related to the column and row position of element 1 in Hqc,gc, we transform the sparse check matrix Hqc,gc into two one-dimensional matrices, which contain the column and row positions of elements 1 in the Hqc,gc matrix. For a clear expression, we use an example to illustrate the process of the matrix transformation. Assume that the matrix H is shown below

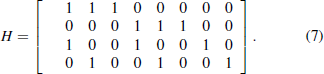
After the process of “distillation”, we use one-dimensional vector row and col to represent the position of elements of 1 in matrix H.

The vector M represents the row position of each element 1 in the matrix H and the vector N represents the column position of each element 1 in the matrix H. Figure 5 presents the decoding speed of the BP algorithm and the BP algorithm using distillation with a code length range from 1000 bits to 14000 bits in a Intel Core i5-8400 CPU and an NVIDIA Tesla K80 GPU. In GPU-based decoding process, we first copy the message of row keys from CPU to GPU. Then we initialize the message of CNs and VNs. Next we update message of CNs and VNs using horizontal step and vertical step. After reaching the maximum number of iterations I or successful decoding, we get decoded data using Eq. (6) and copy them from GPU to CPU. In the reverse reconciliation process, we use the structural characteristics of CN-based QC-GC-LDPC code as shown in Fig. 1. First, we decode the received data in the local decoder. When the decoding fails and the number of iterations IL of the local decoders is reached, the failed data are sent to the global decoder for secondary decoding, which can reduce FER and improve reconciliation efficiency. The decoding speed using distillation reaches 0.68 Mbits/s in an Intel Core i5-8400 CPU and reaches 23.8 Mbits/s in an NVIDIA Tesla K80 GPU. We know that the decoding speed of the BP algorithm will increase after using distillation.

Fig. 5. The decoding speed about BP algorithm and BP algorithm using distillation. The decoding speed of BP algorithm using distillation reaches 0.68 Mbits/s in an Intel Core i5-8400 CPU, which is better than BP algorithm. The decoding speed reaches 23.8 Mbits/s in an NVIDIA Tesla K80 GPU. The blue columnar bar represents the decoding speed mentioned in Ref. [4].

Thus, using distillation will affect the decoding process, which means that the two-dimensional matrix is involved during decoding. The two-dimensional matrix is characterized by L(rji) and L(qij), respectively. After distillation, the L(rji) and L(qij) introduced in Subsection 2.3 are represented by L(rn) and L(qn).

where M(n) and N(n) are the row and column position look-up tables.

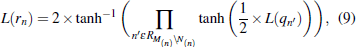
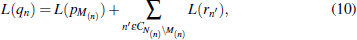
We should notice that the range of subscripts i in Eq. (4) and Eq. (5) is different from subscripts n in Eq. (9) and Eq. (10). The size of L(rji) and L(qij) is m × n (the size of matrix H), while the size of L(rn) and L(qn) is P, where P is the number of element 1 in H. Distillation brings the benefit of improving the speed of decoding. Besides, distillation can decrease the cost of memory due to the sparsity of matrix H. The sparsity of H matrix leads to high complexity in the reverse reconciliation. We use distillation to reduce the computational complexity, which is used to extract 1 elements of H matrix. The decoding speed of the reverse reconciliation using distillation can achieve 23.8 Mbits/s in an NVIDIA Tesla K80 GPU.

3.2. Secret key rate and low frame error rate

As described in Subsection 2.3, in the reverse reconciliation, the codeword of Bob is sent to Alice the error correction in the form of frame U. if the result of the calculation is , the decoding fails. In order to express the possibility of decoding failure, we introduce the frame error rate (FER). The FER is one of the most critical parameters of an error-correcting code, since decoding a message failure is usually associated with data loss in conventional data transmission scenarios, resulting in retransmission delays, that is, the original key blocks decoded incorrectly are discarded by Bob and Alice in the CV-QKD system. Based on base graph 1 in 5G standard, we construct a parity check matrix Hqc,gc of size 21712 × 32096 and code rate 0.3235.[49] Figure 6(a) shows the performance of the CN-based QC-GC-LDPC codes in terms of the BER, where the BER of code length 32096 can reach 5.45 × 10–7. Figure 6(b) shows the performance of the FER about the CN-based QC-GC-LDPC codes, where the FER of code length 32096 can reach 3.25 × 10–3. In Fig. 6(a), we can see that the performance of the BER increases as the code length increases of the same code. Figures 6(c) and 6(d) show the performances of BER and FER under different iterations. When the code length is infinite, the decoding speed will be slow due to the computing power of the CPU, so the code length we used is 32096. As a result, the finial key rate will be affected by (1 − FER), and the secret key rate[46,50,51] of the reverse reconciliation under collective attack can be represented as

where β is the efficiency of the reverse reconciliation using CN-based QC-GC-LDPC codes, IAB denotes the Shannon mutual information of Alice and Bob, which is numerically equal to the capacity of the channel. χBE denotes the Holevo bound on the information between Bob and Eve.[52–54]

where V = VA + 1, VA is modulation variance of Alice, and χtotal is the total noise between Alice and Bob. The Holevo bound χBE is

where G(x) = (x + 1) log2 (x + 1) − x log2x, the λ1,2,3,4,5 are given by and , λ5 = 1, where

where χh is the additive noise of the detector which is attributed to the channel input. χh = [(1 − η) + vel]/η, where η represents the quantum efficiency of detection of Bob, and vel is the detector electrical noise. T is the transmittance of the CV-QKD system. The χline is the channel additive noise which attributed to the input, χline = 1/T − 1 + ξ, where ξ is the system noise.

Fig. 6. (a) The BER performance of CN-based QC-GC-LDPC codes over AWGN channel. The BER can reach 10–7 using the Belief-propagation decoding algorithm. (b) The FER performance of CN-based QC-GC-LDPC codes over AWGN channel. The FER can reach 10–3 using the Belief-propagation decoding algorithm. (c) The performance of BER for different iterations. This figure shows the BER with 75, 35, and 15 iterations. As the number of iterations increases in the reverse reconciliation, the BER is more accurate. (d) The performance of FER under different iterations. This figure shows the FER with 75, 35, and 15 iterations. As the number of iterations increase in the reverse reconciliation, the FER is more accurate.
3.3. Reconciliation efficiency

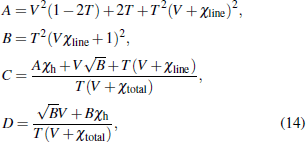
Although the error correction problem has never been a critical issue for DV-QKD protocol, it only contains a small correction item, error correction is necessary for a CV-QKD protocol. For CV-QKD protocol, Alice and Bob need to extract their mutual information IAB effectively. According to Eq. (11), the reconciliation efficiency affects the generation of the secret key rate. According to Eq. (15), the calculated reconciliation efficiency of our proposal is 95.42%, which is better than the one proposed in Refs. [46,50]. The reconciliation efficiency βqc,gc can be expressed as

where Rcode is the code rate which is equal to k/n from the k-length information M and codeword U of length n, C(s) is the Shannon capacity and C(s) = 1/2log2(1 + s) in which s is the SNR of the AWGNC[15,55] and s = 1/σ2, σ2 is the noise variance.

The CN-based QC-GC-LDPC codes are descried in Ref. [40], the code rate is 0.4924 and the SNR Shannon limit is 1.12, using Eq. (15) we can gain the reverse reconciliation efficiency 90.8%. In order to improve the efficiency of the reconciliation, we need to reduce the code rate to increase the amount of redundant information. We briefly introduce the method of reducing the code rate via repetition coding mentioned in Ref. [56]. Starting with the repeat-accumulate (RA) code, additional rows and columns are appended as shown in Eq. (16). The matrix I is the identity matrix (ones on the diagonal, zeros elsewhere), and the matrix 0 is an all zero matrix. The matrix E can be formed from the first two columns of a truncated Vandermonde matrix. In our paper, we use repeat-accumulate codes[56] to reduce the GC-LDPC code rate to 0.3235 and SNR is 0.6 and we obtain the reverse reconciliation efficiency 95.42%. As shown in Table 1, using GC-LDPC codes provides higher efficiency of the reverse reconciliation.

Table 1.

The efficiencies of the reverse reconciliation in the proposed and the previous reconciliation schemes.

.
4. Conclusion

In this paper, we introduced the reverse reconciliation of CV-QKD system using CN-based QC-GC-LDPC codes. It was shown that the proposed scheme can provide more efficiencies and reduce the BER and FER in the reverse reconciliation. Given high complexity of the sparsity of check matrix in the reverse reconciliation, we use distillation to reduce the computational complexity, and the decoding speed of reconciliation can achieve 23.8 Mbits/s. Low FER and high decoding speed enable the CV-QKD system to quickly complete quantum key distribution. The excellent performance of CN-based QC-GC-LDPC codes can be applied in high-speed CVQKD system.

Reference
[1] Gisin N Ribordy G Tittel W Zbinden H 2002 Rev. Mod. Phys. 74 145
[2] Wang X Y Zhang Y C Yu S Guo H 2018 Sci. Rep. 8 10543
[3] Scarani V Bechmann-Pasquinucci H Cerf N J Dušek M Lütkenhaus N Peev M 2009 Rev. Mod. Phys. 81 1301
[4] Lin D K Huang D Huang P Peng J Y Zeng G H 2015 Int. J. Quantum. Inf. 13.02 100501
[5] Qian Y J He D Y Wang S Chen W Yin Z Q Guo G C Han Z F 2019 Optica 6 1178
[6] Wang S Chen W Yin Z Q He D Y Hui C Hao P L Fan-Yan G J Wang C Zhang L J Kuang J Liu S F Zhou Z Wang Y G Guo G C Han Z F 2018 Opt. Lett. 43 2030
[7] Wang S Yin Z Q Chau H F Chen W Wang C Guo G C Han Z F 2018 Quantum Science and Technology 3 025006
[8] Wang S He D Y Yin Z Q Lu F Y Cui C H Chen W Zhou Z Guo G C Han Z F 2019 Phys. Rev. 9 021046
[9] Yin Z Q Wang S Chen W Han Y G Wang R Guo G C Han Z F 2018 Nat. Commun. 9 457
[10] Wang S Yin Z Q Chen W He D Y Song X T Li H W Zhang L J Zhou Z Guo G C Han Z F 2015 Nat. Phoron. 9.12 832
[11] Wang S Chen W Guo J F Yin Z Q Li H W Zhou Z Guo G C Han Z F 2012 Opt. Lett. 37 1008
[12] Wang S Chen W Yin Z Q Li H W He D Y Li Y H Zhou Z Song X T Li F Y Wang D Chen H Han Y G Huang J Z Guo J F Hao P L Li M Zhang C M Liu D Liang W Y Miao C H Wu P Guo G C Han Z F 2014 Opt. Express 22 21739
[13] Assche G V Cardinal J Cerf N J 2004 IEEE Trans. Inf. Theory 50 394
[14] Furrer F 2014 Phys. Rev. 90 042325
[15] Milicevic M Chen F Zhang L M Gulak P G 2018 Npj. Quantum Inform. 4 21
[16] Diamanti E Lo H K Qi B Yuan Z 2016 Npj. Quantum Inform. 2 16025
[17] Huang D Huang P Li H S Wang T Zhou Y M Zeng G H 2016 Opt. Lett. 41 3511
[18] Huang D Huang P Wang T Li H S Zhou Y M Zeng G H 2016 Phys. Rev. 94 032305
[19] Jouguet P Kunz-Jacques S Leverrier A Grangier P Diamanti E 2013 Nat. Photon. 7 378
[20] Tang G Z Sun S H Li C Y 2019 Chin. Phys. Lett. 36 70301
[21] Jiang X Q Huang P Huang D Lin D K Zeng G H 2018 Phys. Rev. 95 022318
[22] Bennett C H Brassard G 1984 Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing Bangalore, India 175
[23] Guo Y Su Y Zhou J Zhang L Huang D 2019 Chin. Phys. 28 010305
[24] Wang C Huang P Huang D Lin D K Zeng G H 2016 Phys. Rev. 93 022315
[25] Lu Z X Yu L Li K Liu B C Lin J G Jiao R Z Yang B J 2010 Sci. China-Phys., Mech. Astron. 53 100
[26] Zhang H Mao Y Huang D Guo Y Wu X Zhang L 2018 Chin. Phys. 27 090307
[27] Li D W Huang P Zhou Y M Li Y Zeng G H 2018 IEEE Photon. J. 10.5 1
[28] Jiang X Q Huang P Huang D Lin D K Zeng G H 2017 Phys. Rev. 95 022318
[29] Bacco D Canale M Laurenti N Vallone G Villoresi P 2013 Nat. Commun. 4 2363
[30] Huang D Lin D K Wang C Wei W Q Fang S H Peng J Y Huang P Zeng G H 2015 Opt. Express 23 017511
[31] Bai Z L Wang X Y Yang S S Li Y M 2016 Sci. China-Phys. Mech. Astron. 59 614201
[32] Jouguet P Kunz-Jacques S Diamanti E Leverrier A 2012 Phys. Rev. 86 032309
[33] Leverrier A Grosshans F Grangier P 2010 Phys. Rev. 81 062343
[34] Kiktenko E O rushechkin A S Lim TC C W Kurochkin Y V Fedorov A K 2017 Phys. Rev. Appl. 8 044017
[35] Leverrier A Grangier P 2011 Phys. Rev. 83 042312
[36] Jouguet P Kunz-Jacques S 2012 arXiv: 1204.5882
[37] Li Y M Wang X Y Bai Z L Liu W Y Yang S S Peng K C 2017 Chin. Phys. 26 040303
[38] Li J Lin S Abdel-Ghaffar K Ryan W E Costello D J 2016 IEEE Inform. Theory Appl. Workshop 16777097
[39] Phromsa-ard T Sangwongngam P Sripimanwat K Kaemarungsri K Vanichchanunt P Wuttisittikulkij L 2014 IEEE Electron., Comput., Telecommun. Inform. Technol. 1 5
[40] Zhang J Bai B Mu X Xu H Liu Z Li H 2018 Wirel. Commun. Mob. Com. 14 4397671
[41] Diao Q Huang Q Lin S 2012 IEEE Trans. Inf. Theory 58 4030
[42] Jouguet P Elkouss D Kunz-Jacques S 2014 Phys. Rev. 90 042329
[43] Grosshans F Van Assche G Wenger J Brouri R Cerf N J Grangier P 2003 Nature 421 238
[44] Fossorier M P C Mihaljevic M Imai H 1999 IEEE Trans. Inf. Theory 47.5 673
[45] Gallager R 1962 IEEE Trans. Inf. Theory 8.1 21
[46] Lodewyck J Bloch M Garciá-Patroán R Fossier S Karpov E Diamanti E Debuisschert T Cerf N J Tualle-Brouri R Mclaughlin S W 2007 Phys. Rev. 76 042305
[47] Jiang X Q Yang S Y Huang P Zeng G H 2018 IEEE Photon. J. 10.4 1
[48] Mackay D J 1999 IEEE Trans. Inf. Theory 45 399
[49] Document 3GPP R1-1711982 3GPP TSG RAN WG1 Meeting AH NR2, 3GPP, June 2017
[50] Leverrier A Alléaume R Boutros J Zémor G Grangier P 2008 Phys. Rev. 77 042325
[51] Huang D Huang P Wang T Li H S Zhou Y M Zeng G H 2016 Phys. Rev. 94 032305
[52] Fossier S Diamanti E Debuisschert T Tualle-Brouri R Grangier P 2009 J. Phys. 42 114014
[53] Huang D Huang P Lin D K Zeng G H 2016 Sci. Rep. 6 19201
[54] Guo Y Liao Q Wang Y Huang D Huang P Zeng G H 2017 Phys. Rev. 95 032304
[55] Jouguet P Kunz-Jacques S Leverrier A 2011 Phys. Rev. 84 062317
[56] Johnson S J Chandrasetty V A Lance A M 2016 IEEE Australian Communications Theory Workshop 18 23