† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61703312 and 61703313).
The finite-time Mittag–Leffler synchronization is investigated for fractional-order delayed memristive neural networks (FDMNN) with parameters uncertainty and discontinuous activation functions. The relevant results are obtained under the framework of Filippov for such systems. Firstly, the novel feedback controller, which includes the discontinuous functions and time delays, is proposed to investigate such systems. Secondly, the conditions on finite-time Mittag–Leffler synchronization of FDMNN are established according to the properties of fractional-order calculus and inequality analysis technique. At the same time, the upper bound of the settling time for Mittag–Leffler synchronization is accurately estimated. In addition, by selecting the appropriate parameters of the designed controller and utilizing the comparison theorem for fractional-order systems, the global asymptotic synchronization is achieved as a corollary. Finally, a numerical example is given to indicate the correctness of the obtained conclusions.
Over the past decade, the integer-order memristive neural networks (IMNN) have been developed in an unprecedented way and widely used in various fields, such as signal and image processing,[1,2] algorithm optimization,[3] classification and automatic control,[4] and so on. At the same time, the relevant dynamic behaviors have also attracted the attention of many scholars.[5–8] As a generalization of integer-order calculus (IC), fractional-order calculus (FC) can be dated back to the 17th century. Compared with IC operators, FC operators not only have hereditary and memory characteristics, but also can increase the degree of freedom to improve the performance of the system. So far, FC has been generally applied in neural networks,[9,10] recognition systems,[11,12] communication systems,[13] viscoelasticity of the material,[14] and so on. What is more important, it is necessary to introduce FC operators into memrisitve neural networks to construct a novel fractional-order memristive neural networks (FMNN), which more accurately describe the dynamic performance of the networks. Some interesting results about FMNN have been investigated, such as Refs. [15–17].
Undeniably, time delays are unavoidable in electronic and electric circuits due to finite switching speed of the amplifiers in electronic components. Moreover, time delays are one of the important reasons producing instability or oscillation of the systems.[18] Taking such facts into account, time delays should be considered in the FMNN. In the published papers,[17,19,20] time delays have been studied as the main considering object. In fact, neurons may have different communication delays, therefore the study on multiple time delays FMNN has more profound theoretical meanings and applications.[21] It is well known that the system parameters may fluctuate within a certain range due to inaccuracy of the model, environmental noise, external disturbances, and other factors. Meanwhile, parameters uncertainty can produce poor dynamic performance for the systems, such as instability, oscillation, chaos, large steady-state error, and so on.
In addition, to the best of our knowledge, the activation functions of many literature[17,22–24] were assumed to be Lipschitz, continuous or continuously differentiable. However, the activation functions of FMNN are usually discontinuous. The main reason is that signal output of neuron and information transmission are discontinuous in actual models.[25,26] In Ref. [25], Forti and Nistri pointed out that the model with discontinuous activation functions can highlight some crucial dynamical behaviors, such as the phenomenon of convergence in finite-time toward the equilibrium point, the presence of sliding modes along discontinuity surfaces, and so on. Considering the fact that various influencing factors could appear when FMNN are applied to the engineering fields such as classification and pattern recognition, it is desirable to explore the dynamical performance about fractional-order delayed memristive neural networks (FDMNN) with parameters uncertainty and discontinuous activation functions.
Synchronization can be regarded as a typical collective behavior, which refers to the coordination of events in a system, and the phenomenon of consistency and unification in time. At noted, synchronization not only can be found in many physical systems, such as power converters and biological systems,[27] but also has been applied to a wide variety of engineering applications like image encryption and information processing.[28] In order to achieve the synchronization, most of the results are obtained to ensure the asymptotic stability of error systems.[29–31] However, asymptotic synchronization denotes that it takes infinite time from the trajectories of the response to the trajectory of the drive system.[22,23,32,33] In fact, it is more desirable for networks to reach synchronization in a finite-time and achieve optimization in convergence time in physical and engineering.[34 – 36] Hence, it is necessary to investigate the finite-time synchronization of FMNN.
Up to now, the finite-time synchronization of FMNN has been studied in previous literature.[37–41] In Ref. [37], by designing a simple linear feedback controller, the finite-time synchronization of FMNN was derived according to Gronwall–Bellmaan inequality. The finite-time synchronization of FDMNN was achieved by utilizing Lyapunov theory, norm properties, and linear feedback controller in Ref. [38]. In Ref. [39], the authors dealt with the finite-time synchronization for a class of FMNN by considering discontinuous activation functions, employing the Young inequality, and applying the fractional-order Lyapunov stability theory. Some sufficient criteria were obtained to ensure the finite-time projective synchronization of FDMNN by utilizing the linear feedback controller and employing Gronwall–Bellman integral inequality and Volterra-integral equation in Ref. [40]. By using Laplace transform, the generalized Gronwalls inequality and linear feedback control technique, the finite-time Mittag–Leffler synchronization of FMNN was achieved in Ref. [41]. However, it is noteworthy that there are few results on the finite-time Mittag–Leffler synchronizations for a class of FDMNN with parameters uncertainty and discontinuous activation functions.
Inspired by the aforementioned discussions, the finite-time Mittag–Leffler synchronization is investigated for fractional-order delayed memristive neural networks with parameters uncertainty and discontinuous activation functions in this paper. Based on non-smooth analysis theory and the properties of fractional-order Lyapunov functions, the synchronization conditions are put forward under the framework of Filippov. The crucial contributions of this paper are at the following aspects:
Compared with previous results, our model considers the parameters uncertainty and discontinuous activation functions. So, our system is more general. By designing a new type of discontinuous feedback controller, some sufficient criteria for the synchronization in finite-time are obtained. Meanwhile, the upper bound of the setting time is explicitly evaluated. By simplifying the designed controller, the asymptotic synchronization of FDMNN with parameters uncertainties and discontinuous activation functions is realized as a corollary. In this paper, the assumptions about activation functions are more general. Moreover, our results extend the existing results in Refs. [19,32,39].
The organization of this paper is summarized as follows. In Section
The relevant properties of Caputo fractional-order derivative are as follows.
In this subsection, a class of FDMNN with the parameters uncertainty and discontinuous activation functions as the drive system is defined by
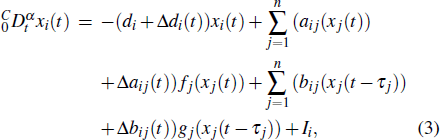

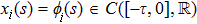
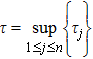
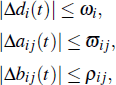
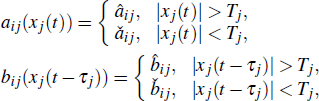
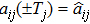
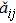


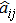



The drive system (
Let the set-valued maps be as follows:
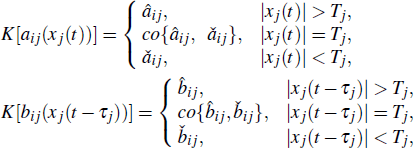
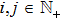
From Assumption 
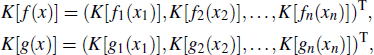

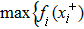
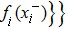


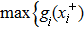

Based on the measurable selection theorem,[46] if xi(t) and yi(t) are a solution of the systems (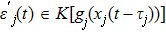


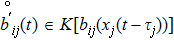
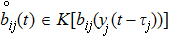
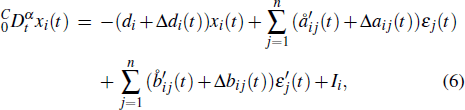
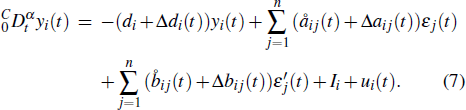
In order to obtain our results, it is necessary to give the following assumption for the discontinuous activation functions.
The synchronization error is defined as e(t) = y(t) − x(t) from the drive system (
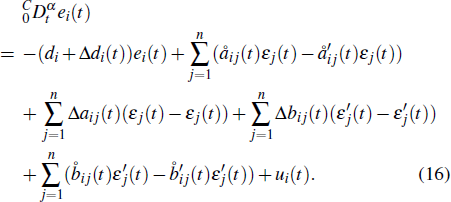
Next, the Mittag–Leffler synchronization of FDMNN with the parameters uncertainty and discontinuous activation functions are obtained by designing a new type of discontinuous feedback controller. In addition, the upper bound of the setting time of the global Mittag–Leffler synchronization in finite-time is explicitly evaluated.
The discontinuous feedback controller ui(t) is defined as
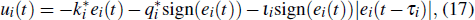
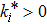
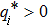
Based on Lemma
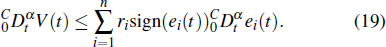
From expressions (
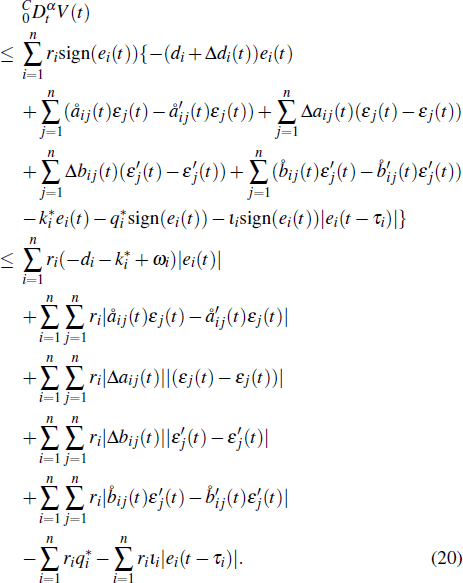
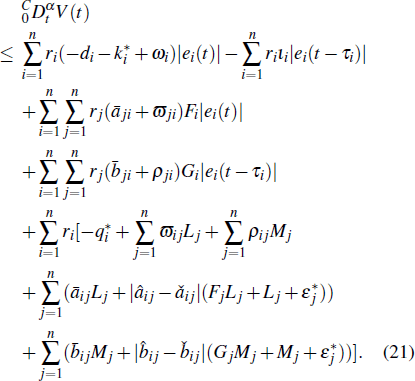
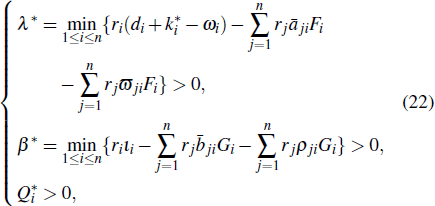
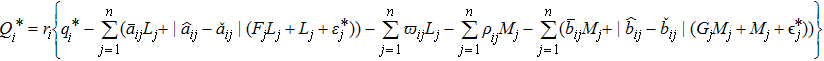
From expressions (
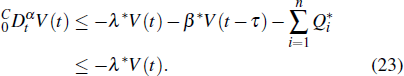
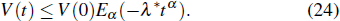
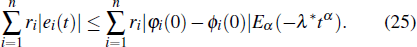
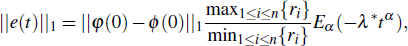
From expressions (
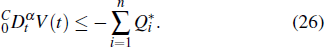
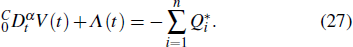

From Definition
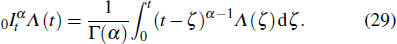
Since Λ(t) ≥ 0 for ζ ∈ [0,t], (t−ζ)α−1 ≥ 0 and Γ(α) > 0. Then

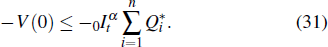
Similarly, based on Definition
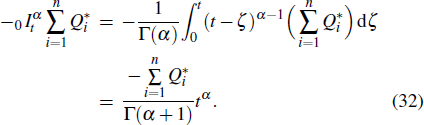
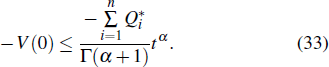

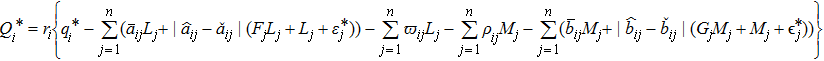
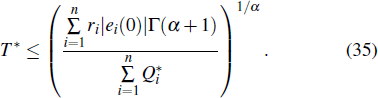
When the parametric uncertainties Δdi(t) = 0, Δaij(t) = 0, and Δbij(t) = 0. As a special case of Theorem
When the parametric uncertainties Δdi(t) = 0, Δaij(t) = 0, and Δbij(t) = 0, and the transmission delays τi = 0. Based on the controller (
When neglecting the effect of ei(t − τi) in expression (
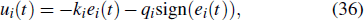
Similar to the above method, one has
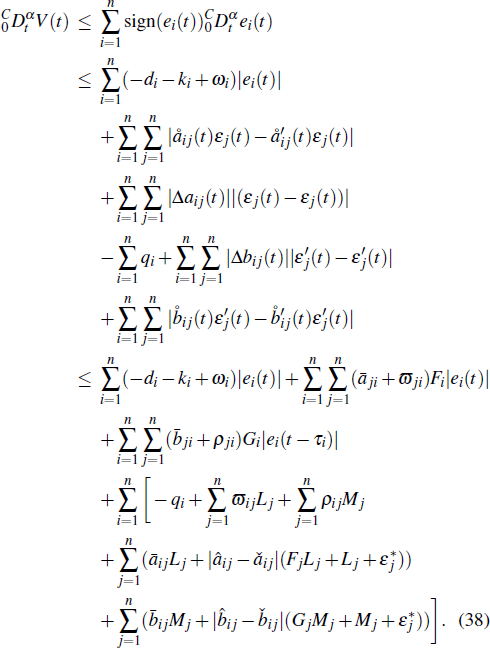
According to Corollary
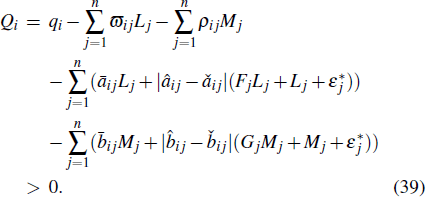
From expressions (

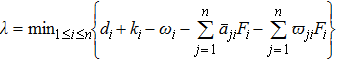
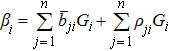
Considering the following system

According to Lemma

Obviously, W* = 0 is an equilibrium point of the system (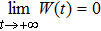
Based on Property
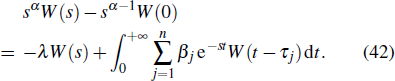
The characteristic equation of the system (
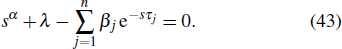
Assuming that equation (

Discussing the real part and imaginary part of Eq. (
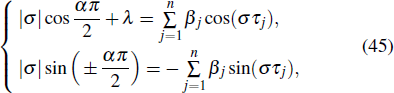
By utilizing the properties of trigonometric functions, we have

Then, combining the real part and imaginary part, one has
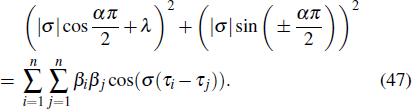
Considering |σ|α as variable of Eq. (

Since 0 < α < 1 and 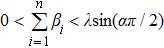
Based on Lemma
In this section, an examples is provided to illustrate the validity of results obtained in this paper.
The parametric uncertainties Δdi(t) = Δaij(t) = Δbij(t) = 0.1 sin(t); The external input I1 = I2 = I3 = 0, and the transmission delays τ1 = 0.1, τ2 = 0.08, and τ3 = 0.11; The initial condition of the system (
Considering the following system as the response system, which is defined by
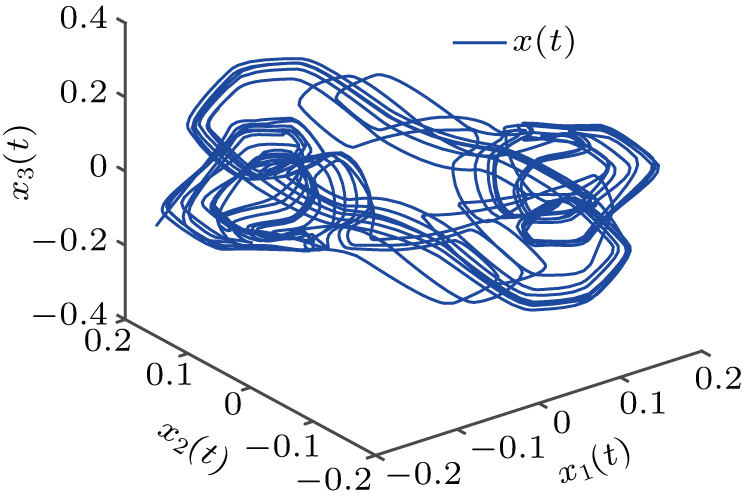
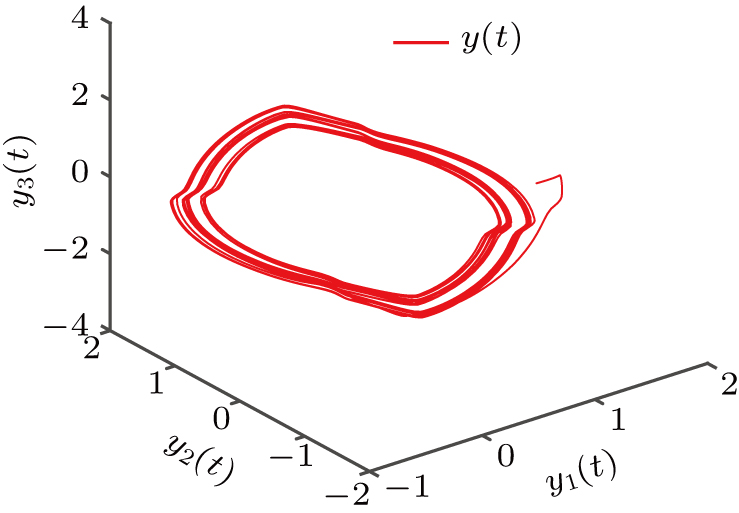 | Fig. 2. Phase plot of response system ( |
In controller (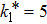
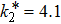
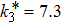
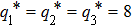
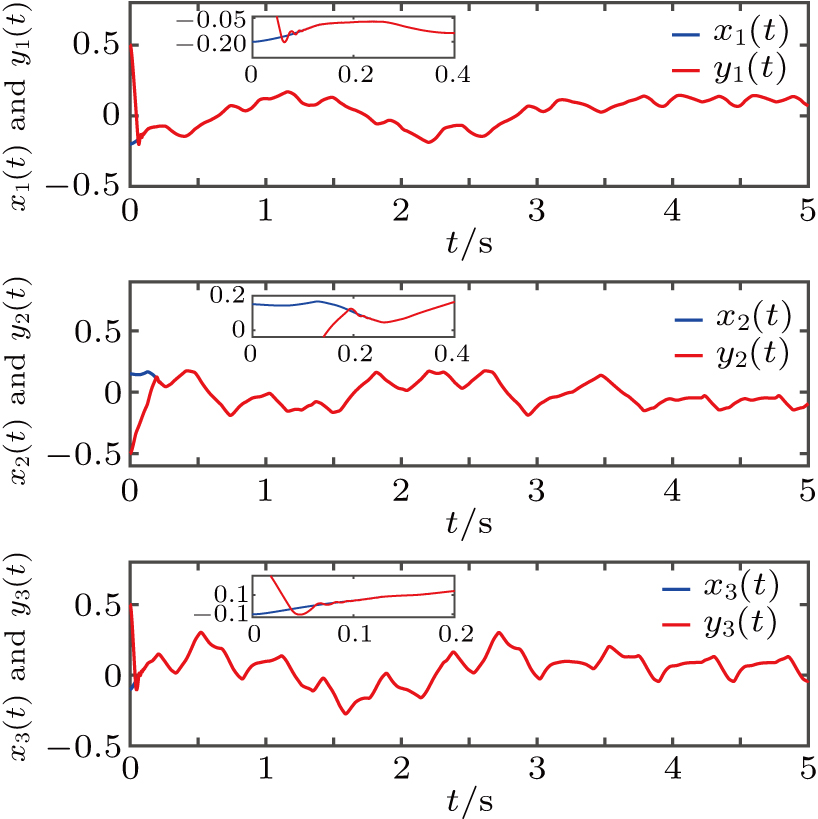 | Fig. 3. State trajectories of drive–response system with the initial conditions x(0) = (−0.2,0.15,−0.1)T and y(0) = (0.5,−0.5,0.5)T under the controller ( |
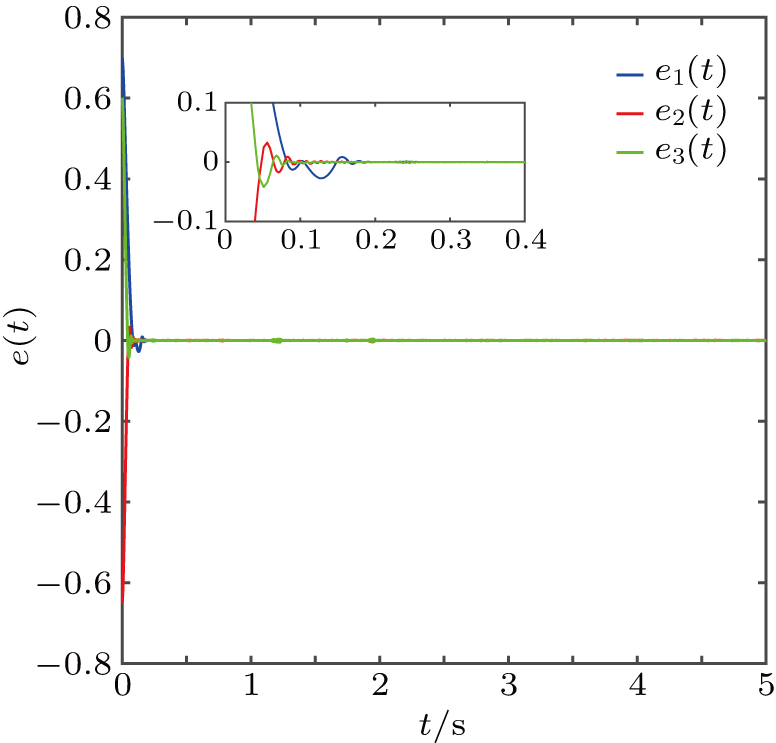
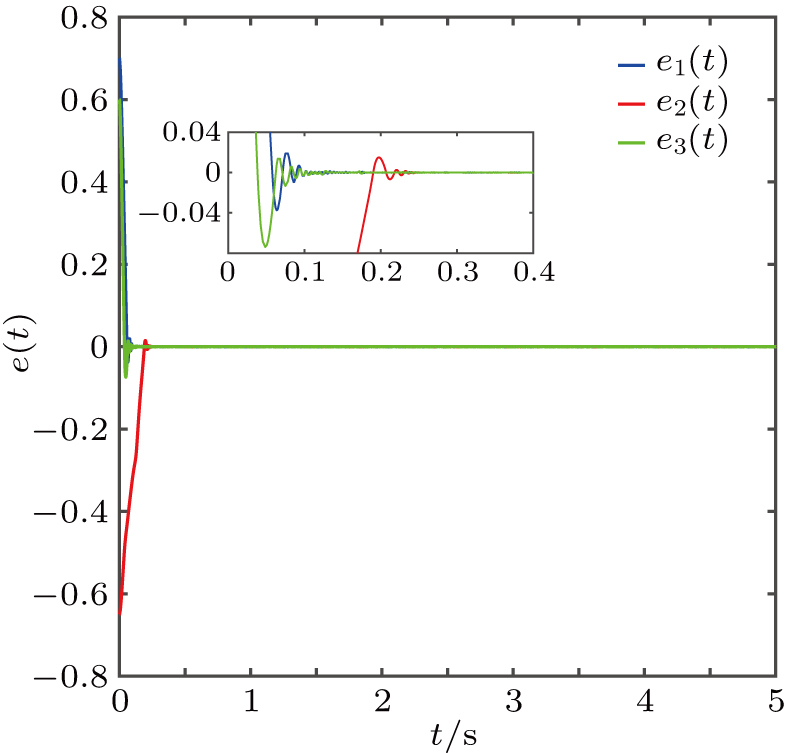 | Fig. 4. State trajectories of synchronization errors e1(t), e2(t), and e3(t) under the controller ( |
In controller (
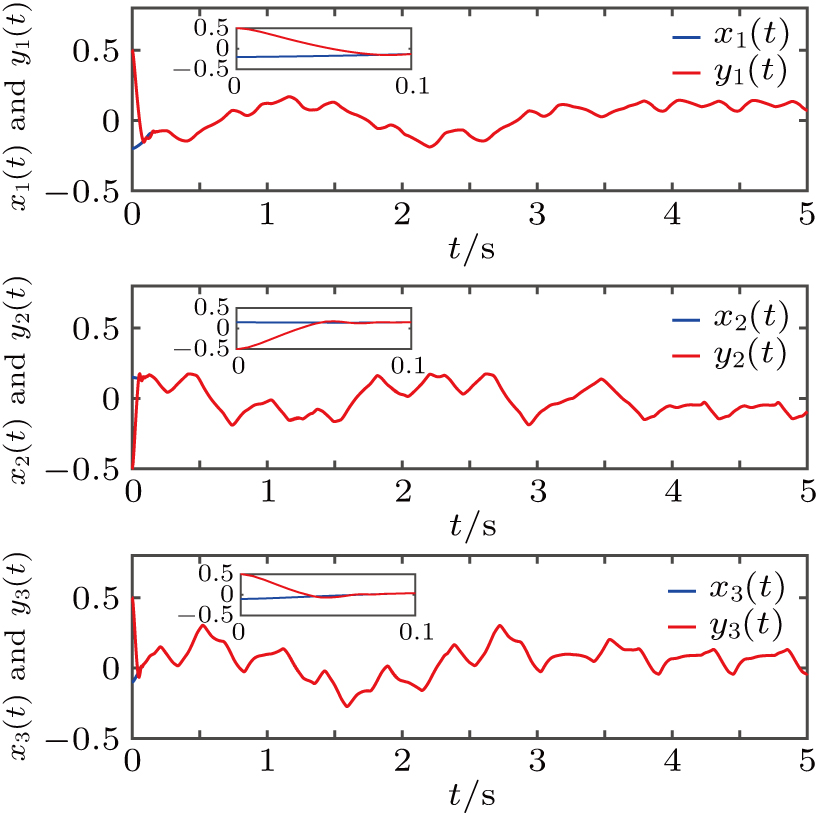 | Fig. 5. State trajectories of drive–response system with the initial conditions x(0) = (−0.2,0.15,−0.1)T and y(0) = (0.5,−0.5,0.5)T under the controller ( |
The finite-time Mittag–Leffler synchronization for a class of FDMNN with parameters uncertainty and discontinuous activation functions has been considered. A series of sufficient conditions ensuring finite-time Mittag–Leffler synchronization of such systems are shown by designing a discontinuous feedback controller. In addition, the asymptotic synchronization has been achieved by using comparison theorem and selecting the appropriate parameters of designed controller. Compared with existing results, the obtained results of this paper are less conservative. It would be interesting to focus on the application of finite-time Mittag–Leffler synchronization of such discontinuous systems in image encryption. This topic goes beyond the scope of this paper and will be a challenging issue for future research.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] |