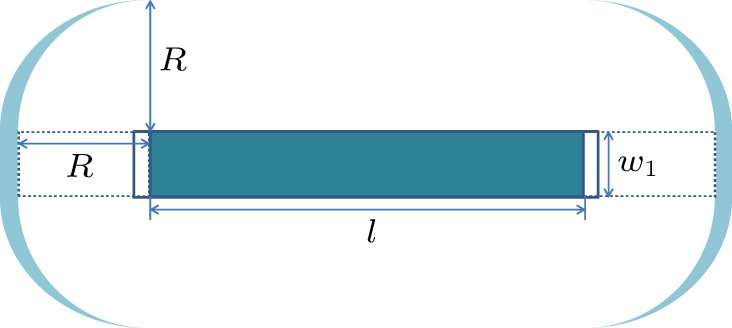† Corresponding author. E-mail:
A new crystal growth theoretical model is established for the low-dimensional nanocrystals on an isotropic and quasi-free sustained substrate. The driven mechanism of the model is based on the competitive growth among the preferential growth directions of the crystals possessing anisotropic crystal structures, such as the hexagonal close-packed and wurtzite structures. The calculation results are in good agreement with the experimental findings in the growth process of the low-dimensional Zn nanocrystals on silicone oil surfaces. Our model shows a growth mechanism of various low-dimensional crystals on/in the isotropic substrates.
Low-dimensional nanocrystals, including nanowires, nanorods, nanobelts, nanoplates, and nanosheets, etc., have triggered numerous fundamental and technological studies for their unique properties in recent decades.[1–3] Using them as active components, various types of nanoscale devices have been fabricated, such as photovoltaic,[4] thermoelectric,[5] and electromechanical[6] devices. The controllable growth of the low-dimensional nanocrystals in terms of the morphologies, sizes and microstructures is urgently desired for their practical applications.
These requirements have led to a rapidly evolving research on the preparation methods and growth mechanisms of the low-dimensional nanocrystals. To our knowledge, vapor deposition including physical vapor deposition (PVD) and chemical vapor deposition (CVD) is one of the most widespread methods for preparing the low-dimensional nanocrystals. Most of the vapor growth processes are based on solid substrates and dominated by the vapor-solid (VS)[2] or vapor-liquid-solid (VLS)[7] mechanism.
For the VS process, the one- or two-dimensional nanocrystals may be controllably fabricated on the well-designed substrates with specific patterns or crystal structures acting as templates.[3, 8, 9] However, the removal of the templates may damage the morphologies and microstructures of the nanocrystals. The well-known VLS growth method uses metal nanoparticles that form low-melting point eutectic alloys with the targeted materials to serve as the catalytic seeds for the one- or two-dimensional crystal growth.[7, 10] Except for the VS growth, the VLS and its variants, such as the vapor-solid-solid (VSS)[11] growth, require the use of suitable catalysts.
Recently, we reported the growth of various low-dimensional zinc (Zn) nanocrystals (for instance, nanowires, nanorods, nanobelts and nanoplates) with two main preferential growth directions of the [0001] and 
According to the theory proposed by Bravais and later modified by Donnay and Harker,[15] the crystal microstructure and morphology are closely related to its intrinsic crystal structure. In this case, the growth rates of the crystal planes are reversely proportional to the reticular densities, i.e., the number of lattice points per unit surface. In other words, there is a growth priority among the crystal planes corresponding to different growth directions, which results in a competitive growth where the crystal planes along the preferential growth directions overgrow the others.
Previous researches showed that the anisotropic crystal structures, such as the hexagonal close-packed (Zn, Be, Mg, Cd, Ti, etc.) and wurtzite (ZnO, ZnS, CdS etc.) structures, usually possess preferential growth directions owing to the asymmetry of these crystal structures.[16–18] To be more exact, a crystal system with relatively less symmetry operations exhibits a stronger preferential growth tendency. For example, compared with those of the hexagonal close-packed and wurtzite structure, the characteristics of preferential growth directions of the face center cubic and zincblende structure are weaker due to their higher symmetry.
On the other hand, the liquid surface can be considered as an isotropic and quasi-free sustained substrate, where the deposition atoms diffuse randomly and freely.[19, 20] The mean square displacement of the deposition atoms is given by 
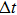
In this paper, we establish a new low-dimensional crystal growth model on the isotropic and quasi-free sustained substrate. The low-dimensional crystal growth does not depend on templates and catalysts, but is driven by the competitive growth among the preferential growth directions of the crystals with anisotropic crystal structures. The model gives a good explanation for the growth process of the low-dimensional Zn nanocrystals on the silicone oil surface. Furthermore, the model indicates the possibility to prepare various low-dimensional crystals on/in the isotropic substrates.
We suppose that atoms are deposited on an isotropic and quasi-free sustained substrate with constant flux f. The low-dimensional crystal growth model is described as follows:
(1) The deposition atoms diffuse freely and randomly on the substrate, then they nucleate and form seed crystals. The morphology of each seed crystal is a cuboid with sizes of 

(2) In the next growth process, the atoms deposited on a seed crystal upper surface and the effective diffusion area 
(3) 



(4) 

(1) One-dimensional crystal growth model (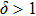
Stage I: 
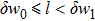
This stage may be considered as a coarsening process of the seed crystal, in which 






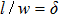



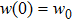




The previous research[19] showed that the diffusion coefficient D of metallic atoms on the silicone oil surface is of the order of 10−11 cm2/s. Therefore, R is nearly 100 nm. The Zn crystals exhibit the hexagonal close-packed crystal structure with two main preferential growth directions, i.e., the [0001] and 




According to expressions (
 | Fig. 2. The growth behaviors of the length and width of the one-dimensional Zn nanocrystals with time at stage I for δ = 12. |
Stage II: 

It can be seen that the growth velocity of the width w has dropped to 0.2 nm/s at the end of stage I. Additionally, in the case of the deposition rate 


At stage II, as shown in Fig. 







Using expression (



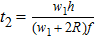
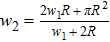
According to expression (
 | Fig. 4. The relationship of the length of the one-dimensional Zn nanocrystals with time at stage II. |
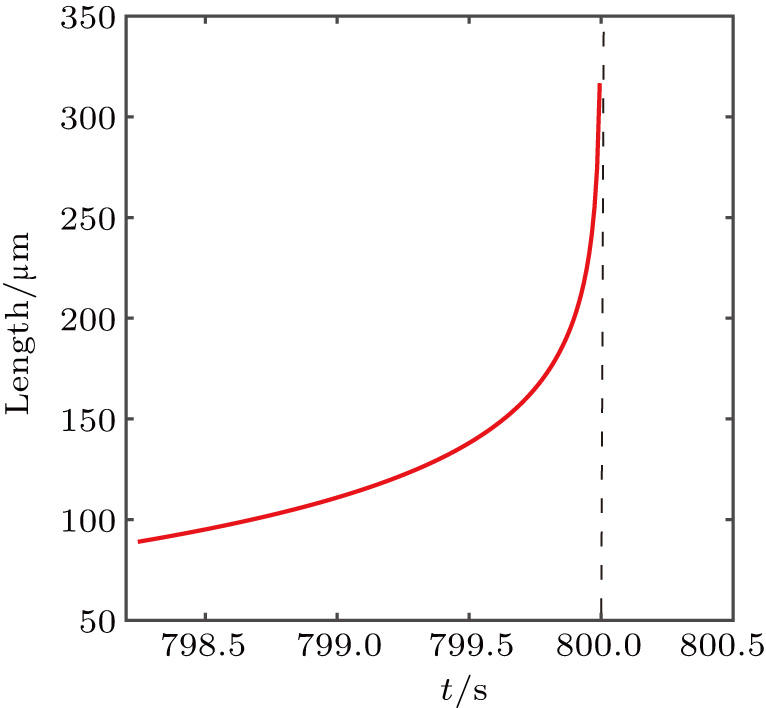
Stage III: 


When 
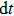
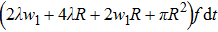




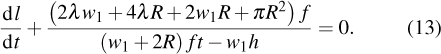

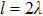




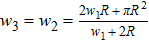
Previous study[25] showed that the effective diffusion length λ of the Zn atoms on the Zn crystal surface is about 39 

Stage IV: 





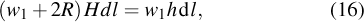


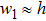
When 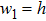



In our experiments,[12] the most probable length range of the one-dimensional Zn nanocrystals is 250–500 nm for 



(2) Two-dimensional crystal growth model (
According to the model described above, the aspect ratio 

Stage I: 


The dependence of the length and width of the two-dimensional Zn nanocrystals on time at stage I for 

Stage II: 
After deposition (
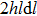




Expression (
The two-dimensional Zn nanocrystals in our experiments include various nanoplates with quadrangular, pentagonal and hexagonal morphologies.[13] In our model, for simplicity, the quadrangular nanoplate is selected as a representative sample to reveal the growth characteristics of the two-dimensional Zn nanocrystals on the silicone oil surface. Actually, the value of δ is closely related to the morphologies of the seed crystals. Therefore, 


In summary, a new low-dimensional crystal growth model is established on the isotropic and quasi-free sustained substrate. The driven mechanism of the model is based on the competitive growth among the preferential growth directions of the crystals with anisotropic crystal structures, which is different from the conventional VS and VLS mechanism. The model gives a good explanation of the growth kinetics of the low-dimensional Zn nanocrystals on the silicone oil surface, i.e., the dependence of the length and width of the one- and two-dimensional Zn nanocrystals on time. Furthermore, the model may be useful to reveal the growth mechanism of various low-dimensional crystals fabricated on the liquid substrates, such as perylene,[27] graphene,[10, 28–30] and hexagonal boron nitride.[31, 32]
In addition, by means of the intrinsic anisotropic crystal structures, many low-dimensional crystals have also been prepared in the liquid environment.[33–35] By further considering the competitive growth in h direction and the mass supply in three-dimensional space, our model may also account for the growth mechanism of various low-dimensional crystals in the isotropic substrates.
We thank Dr. Ziran Ye and Professor Baoxing Li for useful discussions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |