† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2016YFB0700900), the National Natural Science Foundation of China (Grant Nos. 51571126 and 51861030), the Inner Mongolia Autonomous Region Natural Science Foundation of China (Grant No. 2019MS01002), and the Inner Mongolia Innovative Research Team of China (Grant No. 3400102).
Hysteresis loops, energy products and magnetic moment distributions of perpendicularly oriented Nd2Fe14B/α-Fe exchange-spring multilayers are studied systematically based on both three-dimensional (3D) and one-dimensional (1D) micromagnetic methods, focused on the influence of the interface anisotropy. The calculated results are carefully compared with each other. The interface anisotropy effect is very palpable on the nucleation, pinning and coercive fields when the soft layer is very thin. However, as the soft layer thickness increases, the pinning and coercive fields are almost unchanged with the increment of interface anisotropy though the nucleation field still monotonically rises. Negative interface anisotropy decreases the maximum energy products and increases slightly the angles between the magnetization and applied field. The magnetic moment distributions in the thickness direction at various applied fields demonstrate a progress of three-step magnetic reversal, i.e., nucleation, evolution and irreversible motion of the domain wall. The above results calculated by two models are in good agreement with each other. Moreover, the in-plane magnetic moment orientations based on two models are different. The 3D calculation shows a progress of generation and disappearance of vortex state, however, the magnetization orientations within the film plane calculated by the 1D model are coherent. Simulation results suggest that negative interface anisotropy is necessarily avoided experimentally.
Exchange-spring magnets, proposed formerly by Kneller in 1991,[1] have always been an important topic in magnetic materials. These materials have large coercivity and remanence provided by the hard and soft phases, respectively, due to the exchange-coupled interactions between two phases at nanoscale. As a result, the exchange-coupled hard/soft magnets show spring behavior.[2–5] Since Skomski[6] predicted in 1993, via a 1D micromagnetic model, that the energy product can be as large as 1 MJ/m3 in exchange-spring materials with in-plane axes, many experiments have been carried out to reach such a large energy product,[7–11] which has never been achieved. One of the reasons is that the calculation model[6] did not consider the influence of the interface anisotropy, demagnetization, and stray fields on the energy product. However, 3D micromagnetic simulations can give simultaneously the effects of all these factors on the energy product whether easy axes are in-plane or out-of-plane.[12–14]
For realizing such a giant energy product, many works have been carried out in the recent two decades.[15–19] Among them, Cui et al. found that increasing anisotropy behavior can be realized because of preventing effectively interdiffusion by inserting thin non-magnetic spacer layers such as Mo in Nd2Fe14B/α-Fe.[18] In experiments, though the prediction of famous giant energy product is based on parallel-oriented hard/soft multilayers,[19] the largest energy product was presently realized in perpendicular Nd2Fe14B/FeCo multilayers.[20] In most theories, the volume crystalline anisotropy constant Kv, which is independent of the thickness t of the film, is only considered in every layer of hard/soft multilayers.[21–23] On the other hand, the anisotropy of thin magnetic films measured experimentally, varies linearly along with 1/t.[24] Such behavior comes from the two parts of the crystalline anisotropy, that is, the volume crystalline anisotropy constant Kv and the surface crystalline anisotropy constant Ks, whose contribution to the magnetic film anisotropy is 2Ks/t. The interface anisotropy constant in hard/soft multilayers is the sum of the two related surface anisotropy constants.[25,26] The interface anisotropy constants of the transition metals, measured experimentally, may change from positive to negative values[27,28] mainly due to the effect of the material, the lattice orientation and the interface character.
So far, there have been few studies on the influence of interface anisotropy on the magnetic properties of exchange-spring magnets, which are all performed within a 1D micromagnetic framework.[29–31] A 3D micromagnetic calculation can give hysteresis loops, such as the nucleation field, coercivity, energy product, similar to the 1D model. It can also show the magnetic distributions within the film plane, which, however, cannot be described by the 1D model. Within the 1D model, the spin distribution is assumed to be coherent for simplicity. Moreover, the 3D method can give the effect of the stray field on magnetic properties. Therefore, in principle, the 3D model can yield more information and clarify some underlying physical phenomenon of the demagnetization process, which is out of the scope of the 1D model.[12–14] However, unfortunately, there are numerical errors caused by the relatively large mesh sizes adopted in the 3D models, which can be overcome by the 1D model. Also, the most important influence of the interface anisotropy on the magnetic properties, i.e., hysteresis loops and domain walls, are highlighted in the domain wall and its evolution in the thickness direction, which can be described by the 1D model more clearly. Therefore, it is better that both models are used simultaneously and the results are compared with each other to guarantee the reliability. The detailed discussions about these two methods can be found in Refs. [12–14,32,33].
The interface anisotropy is more vital for hard/soft exchange-spring multilayers because they have multiple interfaces. Until now, Nd2Fe14B is the best permanent magnet because of both its high coercivity and saturation magnetization, and hence it has the largest energy product. Moreover, Fe has higher saturation magnetization and can well produce exchange coupling with Nd2Fe14B. Especially, the surface anisotropy values of thin Fe films may change from positive to negative. Experimental results suggest that positive and negative interface anisotropies may occur when the interface of α-Fe is the 100 and 110 planes, respectively. Besides the lattice orientation, the nature of the interface and the temperature have also important influences on the interface anisotropy. More details can be found in Refs. [27,34–36].
In this paper, the effect of interface anisotropy varying from positive to negative values on the hysteresis loop and energy product of a perpendicular Nd2Fe14B/α-Fe multilayer system is studied by the 3D and 1D methods. The results of the two calculated methods are carefully compared with each other. As interface anisotropy increases, the changes of the nucleation field and energy product are always significant for a wide soft layer thickness region, whereas those of the pinning and coercive fields gradually disappear with the increment of the soft layer thickness. Magnetic moment distributions within the film plane and in the thickness direction are given. Our calculated results demonstrate that it is very vital to avoid the negative interface anisotropy in experiments.
An exchange-spring multilayer system is selected as the present calculation model, with hard/soft layers arranged alternatively. As shown Fig.
 | Fig. 1. The basic scheme in this work, with regions calculated from −ts/2 to th/2, which is a simplification of the symmetrical Nd2Fe14B (10 nm)/α-Fe (ts) multilayer. |
We perform both 3D and 1D calculations and make careful comparisons to guarantee the reliability of our results. Meanwhile, the demagnetization progress can be understood better. The 3D simulations are made using the OOMMF software,[38] based on the Landau–Lifshitz–Gilbert (LLG) dynamics equation:[39]

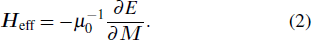

In the 3D simulations, the length and width of both the hard and soft layers are set as 300 nm.[12–14] The length and width of each cell is 3 nm, which is close to the Block wall width of most hard materials. The thickness of each cell is set as 0.5 nm, which has been optimized to achieve a balance between calculation accuracy and computation time. Moreover, the model can also be mimicked better, with the interface anisotropy included in two cells adjacent to the hard and soft layers. Corresponding to the interface anisotropy constant Kint varying from −1 erg/cm2 to 1 erg/cm2 in the 1D calculation, the parameters K of these two cells add Kint in the range from −2.0 × 107 erg/cm3 to 2.0 × 107 erg/cm3 in the 3D simulation. The total thickness of the layers is (th + ts)/2, as shown in Fig.
The above 3D energy could be simplified to a 1D expression, assuming all layers extending to infinity in the direction perpendicular to the z-axis, and the energy density per area in the film plane is[31,41]



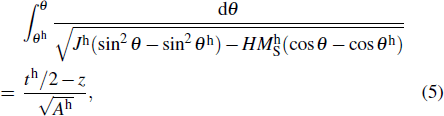


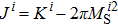
In this paper, Nd2Fe14B and α-Fe are chosen as the hard and soft layers, respectively. The material parameters used in calculations are Ah = 7.70 × 10−7 erg/cm, Kh = 4.30 × 107 erg/cm3, 

Figure
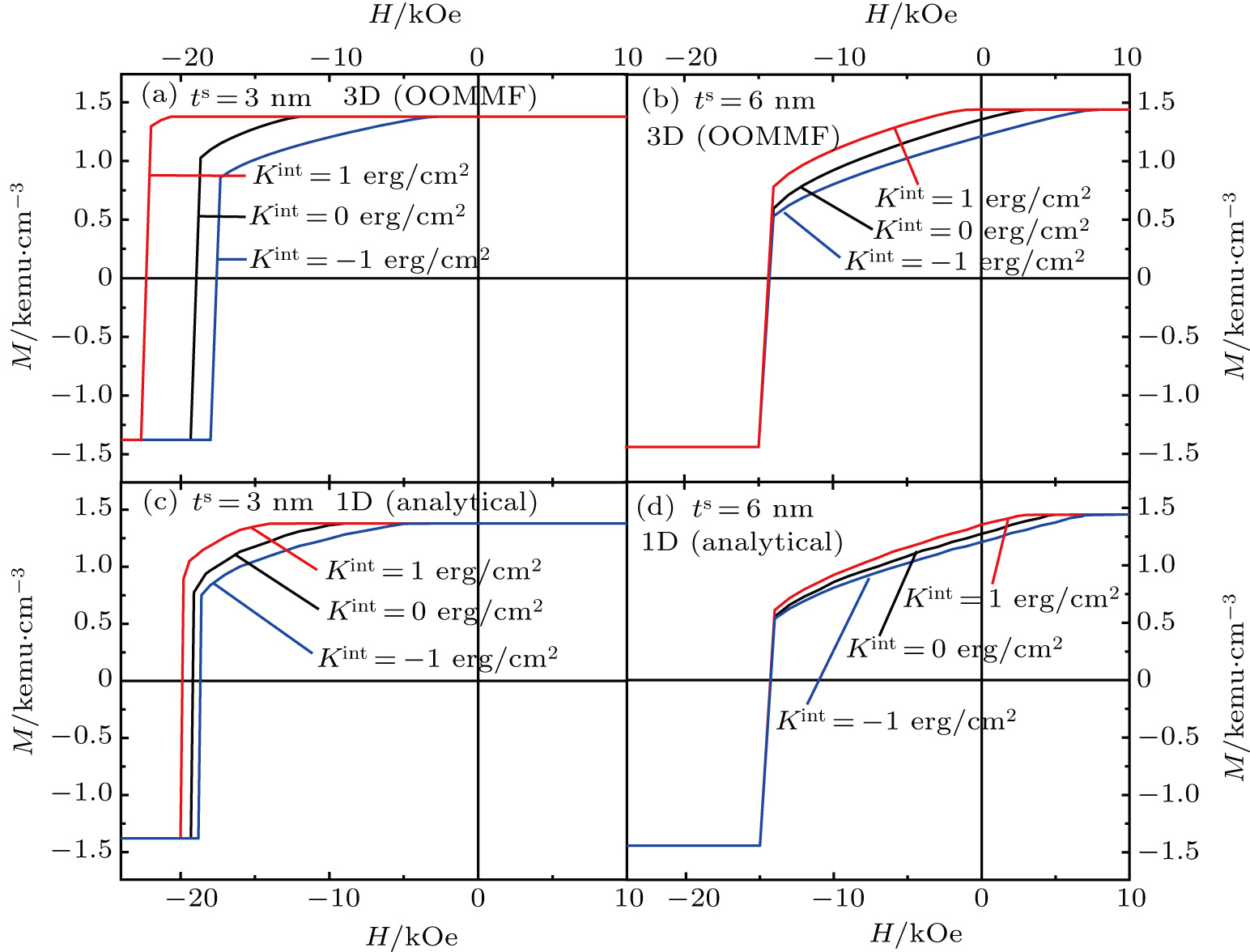 | Fig. 2. Calculated demagnetization curves of Nd2Fe14B (10 nm)/α-Fe (ts) multilayers for various interface anisotropies at ts = 3 nm and 6 nm based on OOMMF (top) and 1D analytical method (bottom). |
As shown in Fig.
The nucleation field calculated by both the methods increases monotonously with Kint for any ts and is close to each other for the same Kint and ts. When Kint = 0 erg/cm2 for any ts, the nucleation field according to OOMMF is slightly larger than that based on the 1D method. Meanwhile, the nucleation field for Kint = 0 erg/cm2 based on two models decreases all with the increment of the soft layer thickness. The latter two results are consistent with those in Ref. [13]. Based on any of the two methods, the soft layer thickness ts has a greater influence on the nucleation field than the interface anisotropy constant Kint. As ts increases, nucleation changes from the second quadrant to the first quadrant, while the nucleation field becomes less dependent on Kint. Even so, when ts is larger, Kint has still a great influence on the nucleation field. As shown in Fig.
The magnetic domain evolution with applied fields and the magnetic reversal mechanism can be visually demonstrated by the angular distribution. The angular distribution θ(z) in the thickness direction has been calculated by the 3D method, as shown in Fig.
As shown in Fig.
As the applied field drops, these prototype domain walls grow fast, while the domain wall decreases with the increase of interface anisotropy. As shown in Fig.
Figure
Though the above angular distribution of magnetizations in the thickness direction has well illustrated the domain wall, the magnetic moment distribution in the film plane at different applied fields should also be discussed for fully revealing the magnetization reversal mechanism. However, in the 1D model, the in-plane magnetic moment distribution is coherent. Based on the 3D simulations, it is interesting to see the formation and change of vortex state in the progress from nucleation to pinning.
Figure
In fact, when ts = 3 nm and 6 nm for any interface anisotropy in the multilayers, such a realized magnetic reversal progress from generation to disappearance of magnetic vortex state based on the 3D model also appears. This means that this process is a general in-plane magnetic reversal mechanism in the 3D model except for the multilayer with very small soft layer thickness, whose hysteresis loop is square and the reversal of the magnetic moments of the whole multilayer is simultaneous (not shown in figure in this paper). The magnetic vortex state observed in this paper was also reported in Ref. [13].
One of the most important properties for permanent magnets is the maximum energy products (BH)max. Based on the data in Fig.
The influence of the interface anisotropy on the magnetic properties of perpendicularly oriented Nd2Fe14B/α-Fe multilayers are researched based on the 3D micromagnetic software OOMMF, and are compared carefully with those calculated by the 1D analytical method. This effect on the coercivity is obvious as the soft layer thickness is small. However, it gradually decreases and last disappears with the increase of the soft layer thickness. The coercivity mechanism is pinning. However, the interface anisotropy always has the large influence on the nucleation field in a wide soft layer thickness range. The nucleation field, coercivity and maximum energy product decrease as the interface anisotropy drops. Therefore, it is important to avoid experimentally the negative interface anisotropy. Moreover, if a giant energy product is to be realized in exchange-spring multilayers, the small soft layer thickness is preferred. The angular distribution in the thickness direction demonstrates that a progress of three-step magnetic reversal, i.e., nucleation, evolution and irreversible motion of the domain wall, exists in the system. The above results calculated by the two methods accord well with each other, confirming that our simulations are correct.
When the hysteresis loop is not square, there is a general magnetic reversal mechanism that the in-plane magnetic moment distribution has a progress of generation and disappearance of magnetic vortex state in the 3D method, whereas there is a coherent distribution in the 1D method. This magnetic vortex state blocks the nucleation, resulting in the increase of the nucleation field of the system. This explains that although the coercivity calculated by the 3D model is smaller than that by the 1D model, the energy product in the 3D calculation is systematically larger than that by the 1D method.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |





