† Corresponding author. E-mail:
Project supported by the National Science Fund for Distinguished Young Scholars, China (Grant No. 51725103) and the National Natural Science Foundation of China (Grant No. 51671193). All calculations have been performed on the high-performance computational cluster in the Shenyang National University Science and Technology Park.
We propose general principles to construct two-dimensional (2D) single-atom-thick carbon allotropes. They can be viewed as the generalization of patterning Stone–Walse defects (SWDs) by manipulating bond rotation and of patterning inverse SWDs by adding (or removing) carbon pairs on the pristine graphene, respectively. With these principles, numerous 2D allotropes of carbon can be systematically constructed. Using 20 constructed 2D allotropes as prototypical and benchmark examples, besides nicely reproducing all well-known ones, such as pentaheptites, T-graphene, OPGs, etc, we still discover 13 new allotropes. Their structural, thermodynamic, dynamical, and electronic properties are calculated by means of first-principles calculations. All these allotropes are metastable in energy compared with that of graphene and, except for OPG-A and C3-10-H allotropes, the other phonon spectra of 18 selected allotropes are dynamically stable. In particular, the proposed C3-11 allotrope is energetically favorable than graphene when the temperature is increased up to 1043 K according to the derived free energies. The electronic band structures demonstrate that (i) the C3-8 allotrope is a semiconductor with an indirect DFT band gap of 1.04 eV, (ii) another unusual allotrope is C3-12 which exhibits a highly flat band just crossing the Fermi level, (iii) four allotropes are Dirac semimetals with the appearance of Dirac cones at the Fermi level in the lattices without hexagonal symmetry, and (vi) without the spin–orbit coupling (SOC) effect, the hexagonal C3-11 allotrope exhibits two Dirac cones at K and K′ points in its Brillouin zone in similarity with graphene.
The experimental realization of graphene has stimulated tremendous research activities on this fascinating two-dimensional (2D) one-atom-thick material[1–13] because of its revolutionary impacts to future industry in many fields, such as energy storages,[15–18] solar cells[19,20] nanoelectronics,[21,22] as well as superconductor.[23–25] Nevertheless, these various applications require versatile and controllable properties upon modifications of the graphene.
Within this context, many two-dimensional single-atom-thick carbon allotropes, called graphene allotropes (GAs), have been proposed. Even before the graphene was confirmed experimentally, one already paid much attention to 2D carbon allotropes. As early as in 1987, some graphynes were theoretically suggested[26] and they were recently demonstrated in details to exhibit the direction-dependent Dirac cones through first-principles calculations.[27,28] In 1994, some other 2D carbon networks were designed for the conjugated-circuit computations.[31] In 1996, one of those proposed 2D networks,[31] later called pentaheptite,[32] composed of pentagons and heptagons, was theoretically claimed to be a metal but with covalent carbon bonds. Just one year later, a 2D net-C structure, composed of the 4y+6+8 membered rings of carbon, was proposed,[33] while in 2000 the Haeckelite structures containing 5+6+7 membered rings of carbons were further presented.[34] Most recently, it was shown that the family of the 5+6+7 membered rings of carbon harbors distorted Dirac cones.[35]
Since graphene was confirmed experimentally,[1,2] the search and study of new GAs was spurred again. Through various nano-engineering defects on the pristine graphene, a class of memberanic carbon allotropes, named dimerite, were conceived.[36,38] Subsequently, based on the defect patterns some 2D carbon allotropes have been proposed,[39] such as octite-SC (5+6+8 membered rings),[40] T-graphene (4 + 8 membered rings),[41] two OPGs (5+8 membered rings),[44] tetrahexcarbon,[92] C10,[93] and net-W (4+6+8 membered rings).[45] In addition, using high-throughput structural searching codes (e.g., CALYPSO[46] and USPEX[47]), numerous GAs (e.g., S- and T-graphene) have also been constructed.[35,48] Recently, a new allotrope with only pentagons, called penta-graphene,[49,50] was proposed. Although many different GAs have been reported, there is still lack of a simple and systematic route to effectively seek structural candidates.
Physically, a fascinating property of graphene is the presence of Dirac cones at the Fermi level. Therefore, the low-energy excitations in graphene are massless Dirac fermions. This peculiar quasiparticle is responsible for many exotic phenomena observed in graphene, for examples, fractional quantum Hall effect[3,14] and ultrahigh carrier mobility.[51] In connection with similar massless Dirac fermions in graphene, it is another frontier of topological Dirac semimetals most in 3D bulk materials, such as Na3Bi and Cd3As2 families,[52–54] and of topological Dirac nodal line semimetals featured by a closed curve by band crossing in analogy with a closed ring formed by Dirac cones, found both in pure metals[55,58,74] and a series of interesting compounds.[56–70] They also exhibit 3D Dirac cones around the Fermi level, inducing exotic properties.[71–78] However, very few 2D Dirac materials are known (see Ref. [79] for a review). The reason is that Dirac cones are topologically protected and robust against perturbations, thus, cannot be obtained by fine tuning the Hamiltonian parameters. This makes discovery of 2D Dirac materials a nontrivial task.
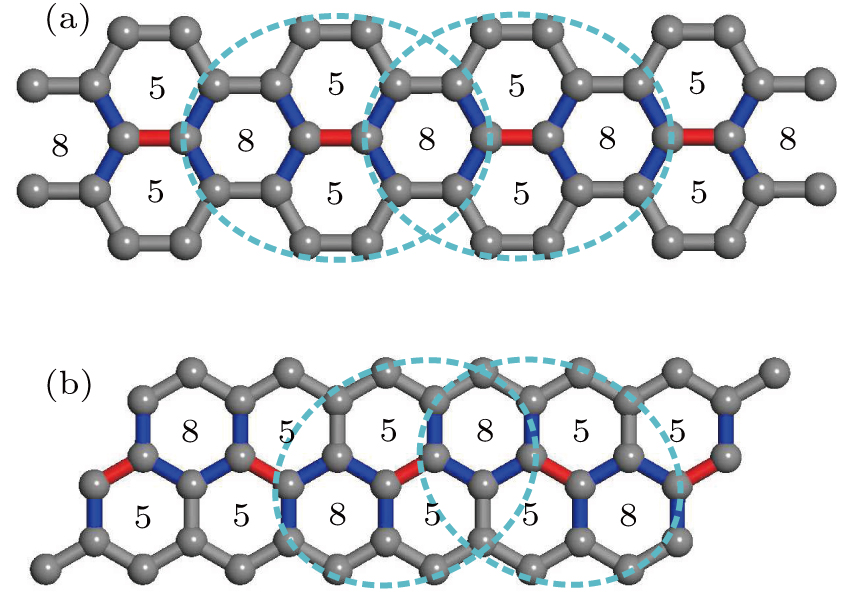
In this paper, we propose general schemes of altering the carbon structure on the pristine graphene. The first one is to implement bond rotation operation, which is a generalization of patterning Stone–Walse defects (SWDs) on the pristine graphene. The second scheme is adding (removing) carbon pairs. This can be viewed as a generalization of patterning inverse SWDs (iSWDs) on the pristine graphene. Based on these two general schemes, we construct numerous 2D carbon networks, including many well-known ones such as pentaheptites,[32] pentahexoctite,[42] T-graphene,[41] OPGs,[44] and so on.[29,43] Moreover, we report many new structures with combinations of other types of membered rings. For these new structures, the formation energies are found to be higher than that of graphene within 1.2 eV per carbon atom. Therefore, they are thermodynamically metastable. However, most of these structures are dynamically stable, due to the absence of imaginary modes in their phonon spectra. Two structures are dynamically metastable. The electronic band structures show that their exhibit various conducting behaviors ranging from metallic, semimetallic to semiconducting. Interestingly, there are four new GAs with massless Fermi fermions due to the presence of Dirac cones at the Fermi level. The C3-11 structure with hexagonal symmetry exhibits an isotropic linear dispersion near K(K′) point, which mimics the case in graphene. The other three new GAs without hexagonal symmetry have anisotropic linear low-energy excitations. These results dispute the long-standing belief that the presence of Dirac cones in graphene is related to its hexagonal symmetry. Our results show that the 2D carbon system is a fertile ground for searching for Dirac materials.
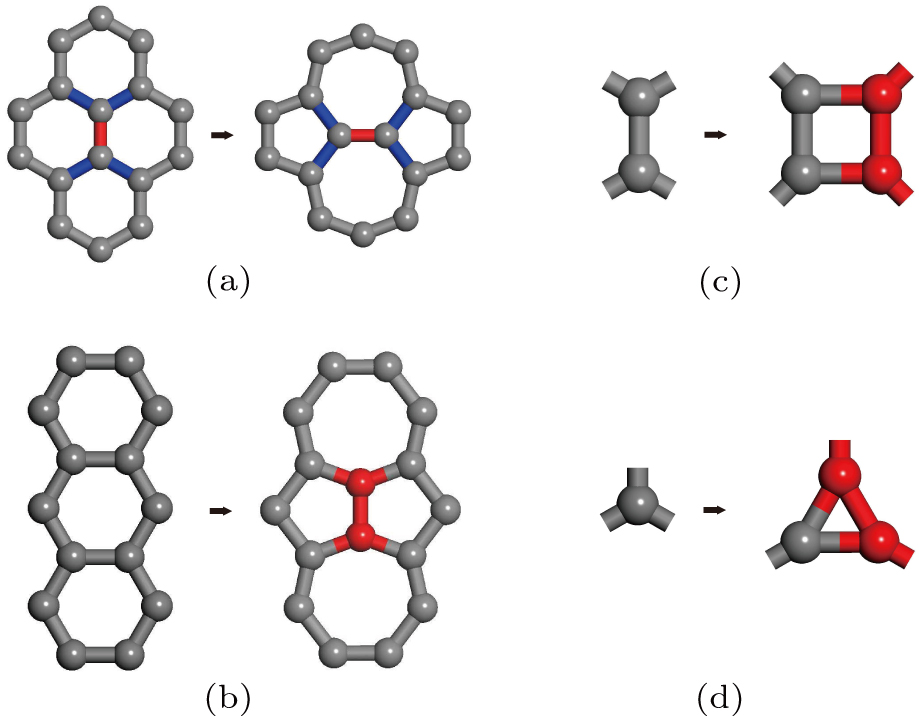
It is well-known that there are two fundamental defects on graphene: the SWD[37] and the iSWD.[38] The formation of a SWD can be understood by rotating the interior carbon–carbon bond in a diamond unit grouped by four adjacent hexagons (Fig.
Here, we propose the first scheme by allowing performing bond rotation on four adjacent any membered carbon rings. The effect of this operation is to extend the two adjacent rings by one atom (i.e., from N1− and N2−membered to N1 + 1 and N2 + 1 -membered rings) while shrink the non-adjacent two rings by one (i.e., from M1 - and M2 -membered to M1 — 1 - and M2 — 1-membered rings). A SWD is a special case where the bond rotation is performed on four adjacent hexagons (i.e., N1 = N2 = M1 = M2 = 6).
There are six carbon–carbon bonds in a hexagon on the pristine graphene. These six bonds form three types of bond pairs: 1) two bonds (of 120°) that share a carbon atom, 2) two bonds (of 60°) that are connected by another carbon bond, 3) two bonds (of 0°) that are parallel to each other. An iSWD is formed when two extra carbon atoms are added to the third kind of bond pair (see Fig.
We perform first-principles calculations based on density functional theory with generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof[81] exchange–correlation functional. All the calculations are performed using Vienna ab initio simulation package (VASP)[82] with projector augmented wave method (PAW).[83] The vacuum slabs of 15Å are chosen to avoid interactions between adjacent carbon layers. A self-consistent field method (tolerance 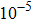
Up till now, we are only looking for new GAs with two types of rings (i.e., 5+7, 4+8, 3+9, 5+8, 4+7, 4+10, 3 + 11, 3 + 12). If more types of rings (i.e., 5 + 6 + 7,4+6+8, etc.) are further taken into consideration, the family of 2D GAs will be significantly enlarged. Following our two schemes, it can be easily done.
| Table 1.
The 2D space group (2sg), Pearson symbol (Ps), optimized DFT lattice constants a, b, angle γ, atom density per area ρ (in atom/Å2), and the formation energy E (in eV/atom) of the selected 2D graphene allotropes. Z counts the number of atoms in the unit cells. E
g is the band gap for semimetals and semiconductors. Y and N in the dynamic column mean dynamically stable and unstable, respectively. |
 | Fig. 4. Phonon spectra and vibrational density of states (VDOS) of graphene allotropes. Two of them ((h) OPG-A and (r) C3-10-H) show imaginary modes. |
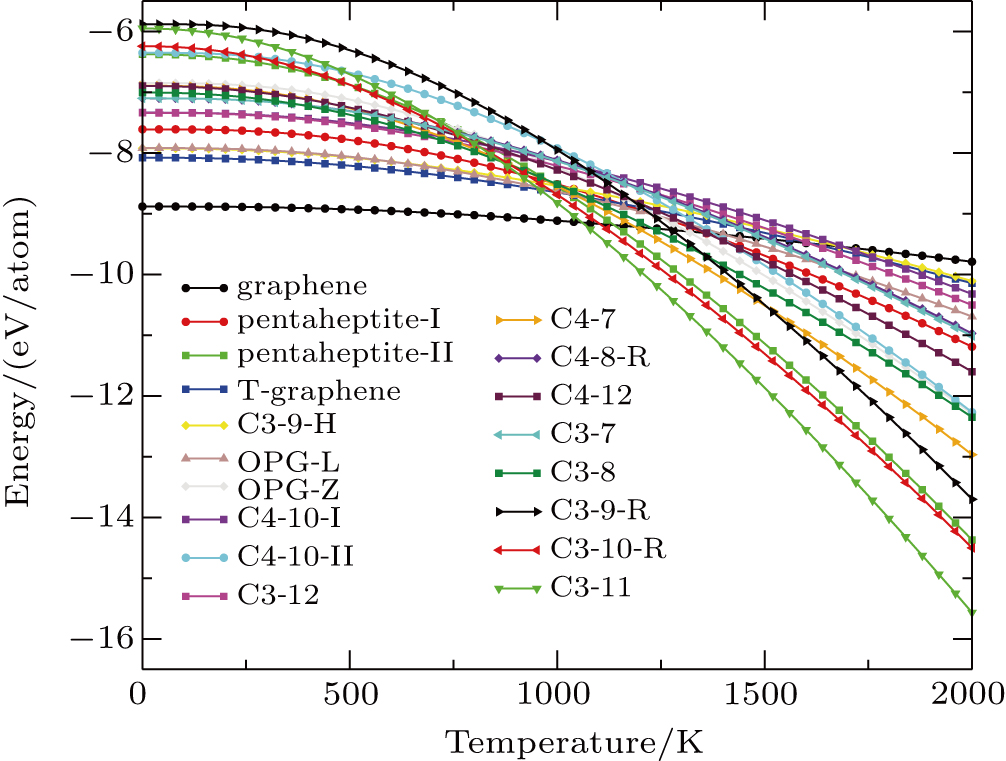 | Fig. 5. The free energy as a function of temperature for GAs. The data for (h) OPG-A and (r) C3-10-H are missing because they are not dynamically stable. |
The Debye temperatures of graphene (2149 K) and Mos2 (610 K) are in good agreement with the values reported in Refs. [95] (2100 K) and [94] (600 K). The effective thickness of all the allotropes is 3.4 Å, which is the distance between two graphite layers. And the bulk and shear moduli of these allotropes are calculated by the isotropic modeling reported in Ref. [80]. Our calculations reveal that the C-11, C3-10-R, and pentaheptite-II allotropes become energetically more favorable than graphene at high temperatures above 1060 K, 1100 K, and 1130 K, respectively. It may suggest the high-temperature phase transformation of the graphene.
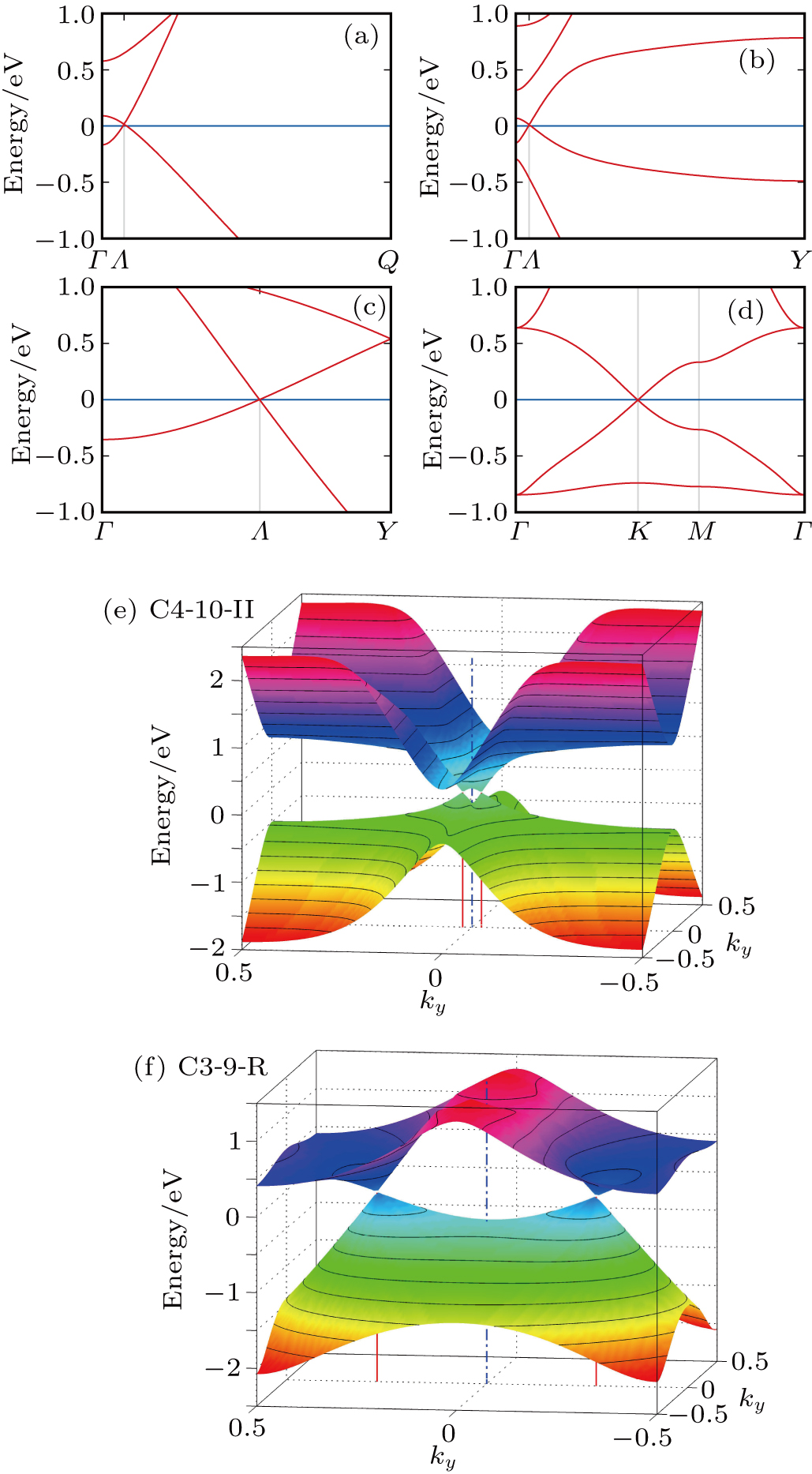
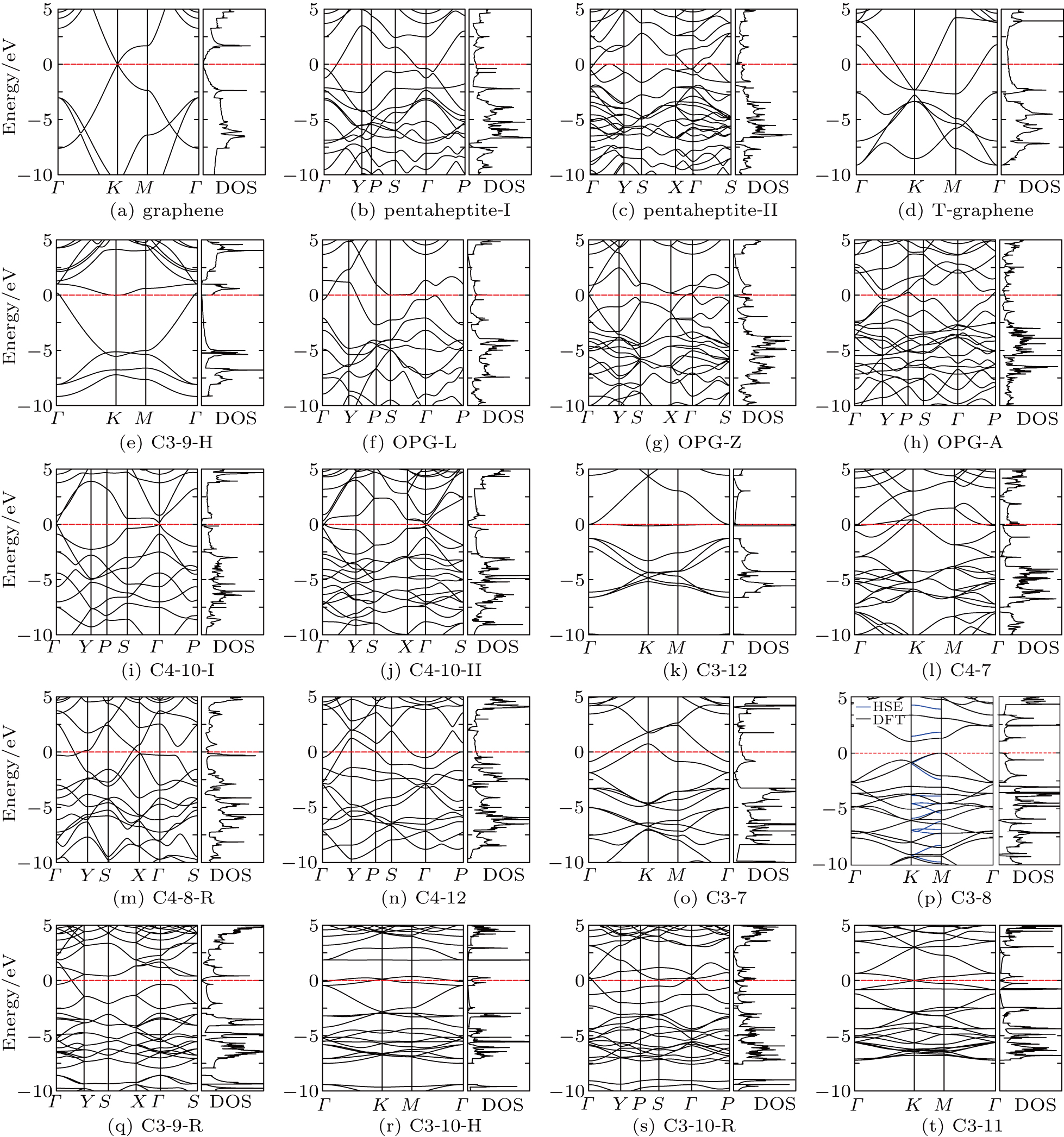 | Fig. 6. Band structures and density of states of graphene allotropes. We have found (p) one semiconductor and (i), (j), (q), (t) four new semimetals. The rest structures are metallic. |
We propose two general constructing schemes of altering carbon structure on graphene. We demonstrate their usefulness by constructing numerous 2D carbon structures. We then study the structural, thermodynamic, dynamic, and electronic properties of these structures. They are all metastable compared to graphene owing to higher formation energies. Two of them ((h) OPG-A and (r) C3-10-H) are dynamically unstable, all other structures are dynamically stable. We have found one semiconductor (C3-8) and four new semimetals (C4-10-I, C4-10-II, C3-9-R, C3-11). C3-11 has isotropic Dirac cones. The other three have anisotropic Dirac cones.
In 2012, Malko et al.[27] found Dirac cones in a 2D carbon system with a rectangular unit cell. Our findings further dispute the suggestion that Dirac cones in graphene are related to its hexagonal symmetry. Indeed, out of 20 simple structures we studied, 4 new and stable structures show band crossing at the Fermi level accompanied with a vanishing electronic density. Three of them do not have a hexagonal unit cell. It shows that Dirac cones in 2D carbon systems are more common than what we previously thought.[35,48,79] Our results show that 2D carbon system is a fertile ground for searching for 2D Dirac materials.
It would be of great interest to experimentally realize these artificial two-dimensional carbon systems. The possible experimental methods include nano-scale defect-engineering on pristine graphene[36,38] and epitaxial or chemical vapor deposition on a substrate.[89,90]
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] |