† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11575033, 11675026, and 11975053) and the Science Foundation from China Academy of Engineering Physics (Grant No. CX2019033).
Taking the Rayleigh–Taylor instability with double interfaces as the research object, the interface coupling effects in the weakly nonlinear regime are studied numerically. The variation of Atwood numbers on the two interfaces and the variation of the thickness between them are taken into consideration. It is shown that, when the Atwood number on the lower interface is small, the amplitude of perturbation growth on the lower interface is positively related with the Atwood number on the upper interface. However, it is negatively related when the Atwood number on the lower interface is large. The above phenomenon is quantitatively studied using an analytical formula and the underlying physical mechanism is presented.
The Rayleigh–Taylor instability (RTI)[1,2] exists widely in inertial confinement fusion (ICF) and supernova explosions. Understanding the mechanism of the RTI is important to the success of the ignition of ICF[3] and to explain the nonlinear evolution of supernova explosions.[4] Generally, it will happen when a heavy fluid is accelerated by a light one, if some perturbations are on the interface between two fluid layers. Focusing on this kind of RTI, many studies have been done in its linear,[1,2] nonlinear,[5,6] and turbulence mixing[7,8] regimes. However, in some practical applications, the RTI with multiple material interfaces is more attractive. For examples, there are an ablator layer, a deuterium–tritium (DT) fuel layer filled with a low density DT gas in the one-shell ICF targets.[9] Alternatively, double-shell targets, which consist of more material layers, were suggested by Amendt[10] and Canaud.[11] Especially, in the implosion process of ICF, the ablation effect makes the material distribution in the capsule more complicated.[12–16] The classic RTI models which only include a single material interface are not good enough for depicting the perturbation growth of the RTI with multiple interfaces. However, to understand the mechanism of the RTI with multiple interfaces, some efforts have been done by researchers. The first series of studies were made by Mikaelian. The author presented an analytical model to describe the temporal evolution of the RTI in the linear growth regime at the interfaces of any number of stratified fluids forming an arbitrary density profile.[17,18] Using this model, some meaningful works have been done by him. For example, the density gradient stabilization effect[19] and the way that how to adjust the perturbation amplitude on the two interfaces to kill the exponentially growing mode.[20] Besides, the author extended the model in the plane geometry to that in the spherical[21] and the cylindrical geometry.[22] Following Mikaelian’s works, the weakly nonlinear growth regime of the RTI was taken into consideration by Wang et al.[23] They presented a weakly nonlinear model of the RTI with a finite-thickness fluid layer. They showed that the weakly nonlinear effect and interface thickness effects are important to understand the flow phenomenons of ICF and supernova explosions. It should be pointed out that this weakly nonlinear model only considers the situation that the Atwood number on the lower interface is 1 and the Atwood number on the upper interface is −1. Focusing on the plane and cylindrical geometry, recently, Guo et al.[24,25] used the potential model to study the linear RTI with multiple fluid layers. Making a summary about the existing studies, one can see that most of studies about the RTI with multiple fluid layers are focussed on in the linear regime. The weakly nonlinear RTI with double interfaces studied by Wang et al.[23] did not cover the situation with varied Atwood numbers. In this study, the situations, the Atwood number on the lower interface is from 0 to 1 and the Atwood number on the upper interface is from −1 to 0, are taken into consideration. The interface coupling effects of the RTI in the weakly nonlinear regime are studied. Euler numerical simulations along with analytical studies are used to do the research in this paper. The results presented in this study are helpful to understand the physical mechanism of the interface coupling effects of the RTI with double interfaces.
The remainder of this article is organized as follows. Firstly, the perturbation interactions between two interfaces are studied by numerical simulations. Secondly, the variation rule of the perturbation amplitude on the lower interface with the Atwood number on the upper interface is studied by the analytical model. Meanwhile, a suppression strategy of the perturbation growth of the RTI on the lower interface is proposed. Thirdly, the underlying mechanisms are explained. Finally, the major conclusions are summarized.
A two-dimensional (2D) problem in the plane geometry, as shown in Fig.
Euler simulations are made in an L × 10L domain containing fluids with three different densities. The domain length in the acceleration direction is 10L. The value of L is 0.01π cm. The acceleration g is 1000 cm/μs2. ρ2 is fixed as 1 g/cm3. In this way, A1 and A2 on the interfaces can be changed by adjusting the values of ρ1 and ρ3. The boundaries at the ends of the y direction are walls. At the ends of x direction, the periodic boundary condition is used. At the initial time, the wavelength on the lower interface is L, and its amplitude is 0.01L. There are 256 uniform grids in the x direction and 2000 grids in the y direction. Most of grids are located in the evolution region of the perturbation. The Euler simulations are done by a well-tested second-order Godunov hydrodynamic simulation code. This code is recently developed in house. The finite volume method and the massively parallel computation are used. The second order HLLE approximation Riemann solver[26] is used. The slope limit is moncen.[27]
To study the interface coupling effects, the temporal evolution of the perturbation growth amplitude on the lower interface (η1) is depicted with some combinations of A1 and A2. Ten situations depicted in Fig.
To further confirm how the interface coupling effects impact on the correlation between η1 and A2, an analytical research is made in the following. Comparing the simulation results and linear analytical results depicted in Fig.
As the line ∂η1(τa)/∂A2 = 0 is nearly linear at different kd, the line can be fixed if positions of points (−1,ya) and (A2 → 0,yb) are known. These points are labeled in Fig.

It should be noted that the values g, η0, and L have no influence on the construction of ∂η1(τa)/∂A2 = 0. As they are eliminated when the value of τa is substituted into ∂η1(τa)/∂A2 = 0. In this way, coefficients a and b in Eq. (
 | Fig. 4. The relationship between A1 and kd under the condition that A2 = −1 and A2 → 0 when ∂η1(τa)/∂A2 = 0 |
It is shown that A1 and kd are nearly exponential relationship when A2 = −1. When A2 → 0, A1 almost has no relationship with kd. Calculating by the data fitting, ya and yb can be defined as 0.289 e−3.252kd +0.678 and 0.396, respectively. Substituting the two points into Eq. (

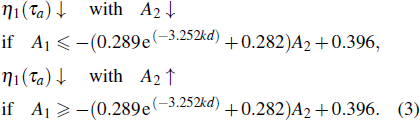
Equations (
Following, the underlying physics mechanism is trying to be described. Firstly, the condition that A1 = 0, which means there is only an upper interface in the system, is concerned. According to the classical linear RTI growth model 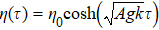
For the RTI with double interface studied in this study, the perturbation seed of the upper interface is from the perturbation evolution on the lower interface. Conversely, the perturbation evolution on the upper interface will impact the perturbation evolution on the lower interface. The downward movement trend of the self-excited response on the upper interface will accelerate the perturbation evolution on the lower interface. The upward movement trend of the self-excited response on the upper interface will suppress the perturbation evolution on the lower interface. It is clear that the value of A1 has influences on the intensity of the perturbation seed of the upper interface, while the value of kd impacts on the generation time of the perturbation seed on the upper interface. Firstly, the rationality of impacts of A1 is concerned. For a small A1, the perturbation intensity generated on the upper interface is small. When the RTI on the lower interface reaches the weakly nonlinear RTI regime, the self-excited response of the upper interface should present the upward movement trend. This trend will suppress the perturbation evolution on the lower interface. As the smaller A2 is, the stronger the trend is. A2 will be positively related to η1. However, for a large A1, the perturbation intensity generated on the upper interface is larger than the situation with a small A1. When the RTI on the lower interface reaches the weakly nonlinear RTI regime, the self-excited response of the upper interface should present the downward movement trend. This trend will accelerate the perturbation evolution on the lower interface. In this way, A2 will be negatively related to η1 when A1 is large. In terms of kd we concerned, one can see that it influences the gradient of the line ∂η1(τa)/∂A2 = 0. The larger the kd is, the smaller the gradient of this line will be. Following, a situation just above the line ∂η1(τa)/∂A2 = 0 in Fig.
The interface coupling effects of the weakly nonlinear RTI with double interfaces are studied by taking into consideration of the two situations: the situation that the Atwood number on the lower interface is from 0 to 1 and the Atwood number on the upper interface is from −1 to 0. This is an expending research of Ref. [23]. It is shown that due to the self-excited response of the upper interface, the amplitude of perturbation growth on the lower interface is positively related with the Atwood number on the upper interface when the Atwood number on the lower interface is small. However, it is negatively related when the Atwood number on the lower interface is large.





